一、有向图方向、权重表示方法
Python通常使用有向图中边的起点和终点来表示边的方向。例如,如果有一条从节点A到节点B的边,则可以使用以下方式表示该有向边:
graph = {'A': {'B': 1}
}
在这个例子中,节点'A'和节点'B'之间存在一条权重为1的边,它的方向是从'A'指向'B'。这表示从节点'A'可以到达节点'B',但不一定反过来。如果要表示从节点'B'到节点'A'的边,需要另外定义一个字典:
graph = {'A': {'B': 1},'B': {'A': 2}
}
在这个例子中,节点'A'和节点'B'之间存在两条边。第一条是从'A'到'B',权重为1,第二条是从'B'到'A',权重为2。注意,这两条边是不同的,因为它们的方向不同。
二、有向图合并原理
有向图合并指的是将多个有向图合并成一个有向图的过程。这种操作在图数据处理中比较常见,例如将多个社交网络中的用户关系、兴趣爱好等信息进行整合,以便进行更全面、准确的分析。
有向图合并的原理主要涉及节点合并和边合并两个方面。
节点合并:当有多个有向图的节点表示同一个实体时,需要将这些节点合并成一个节点,避免在后续操作中出现重复计算问题。节点合并可以使用哈希表等数据结构实现,将每个节点关联到对应的实体上,通过哈希表查找实体对应的节点进行合并。
边合并:当有多个有向图中的两个节点之间存在相同的边时,需要将这些边合并成一条边,以避免重复计算。边合并可以根据具体情况进行不同的处理。例如,如果边的权重值相同,则可以直接合并;如果不同,则可以选择采用加权平均值、加权求和等方法来合并边的权重值。
以下是Python实现有向图合并的示例代码:
def merge_digraphs(graphs):# 合并有向图merged_graph = {}# 记录每个实体对应的节点entity_to_node = {}for graph in graphs:for node, neighbors in graph.items():# 合并节点if node in entity_to_node:curr_node = entity_to_node[node]else:curr_node = nodeentity_to_node[node] = curr_node# 合并边for neighbor, weight in neighbors.items():if neighbor in entity_to_node:curr_neighbor = entity_to_node[neighbor]else:curr_neighbor = neighborentity_to_node[neighbor] = curr_neighborif curr_node not in merged_graph:merged_graph[curr_node] = {}if curr_neighbor in merged_graph[curr_node]:merged_graph[curr_node][curr_neighbor] += weightelse:merged_graph[curr_node][curr_neighbor] = weightreturn merged_grapharr_graph1 = [{'A': {'B': 3, 'C': 6},'B': {'C': 2, 'D': 1},'C': {'D': 1},'D': {}}
]arr_graph2 = [{'A': {'B': 3, 'C': 6},'B': {'C': 2, 'D': 1},'C': {'D': 1},'D': {}},{'A': {'B': 1, 'C': 1},'B': {'C': 1, 'D': 1},'C': {'D': 1},'D': {}}
]
print(merge_digraphs(arr_graph1))
print(merge_digraphs(arr_graph2))运行结果:

graphs是待合并的多个有向图,每个有向图用邻接表形式表示。在合并节点时,首先判断该节点是否已经存在于之前的有向图中,如果是,则直接将当前节点关联到该实体上;否则,将当前节点作为新的节点,并将其关联到对应的实体上。在合并边时,如果两个节点之间的边已经存在,则将其权重值相加;否则,将其作为新的边添加到合并后的有向图中。
三、有向图最长路径算法
下面是一个Python实现有向图最长路径计算的代码示例:
from collections import dequedef topological_sort(graph):# 对有向图进行拓扑排序in_degree = {v: 0 for v in graph} # 记录每个节点的入度for node in graph:for neighbor in graph[node]:in_degree[neighbor] += 1queue = deque([node for node in in_degree if in_degree[node] == 0])result = []while queue:node = queue.popleft()result.append(node)for neighbor in graph[node]:in_degree[neighbor] -= 1if in_degree[neighbor] == 0:queue.append(neighbor)if len(result) != len(graph): # 存在环return Nonereturn resultdef longest_path(graph, start, end):# 计算有向图中从start到end的最长路径topological_order = topological_sort(graph)print(f'有向图拓扑排序结果:{topological_order}')dist = {node: float('-inf') for node in graph}dist[start] = 0prev = {node: None for node in graph}for node in topological_order:if node == end:breakif dist[node] != float('-inf'):for neighbor in graph[node]:new_dist = dist[node] + graph[node][neighbor]if new_dist > dist[neighbor]:dist[neighbor] = new_distprev[neighbor] = node# 生成路径path = []node = endwhile node is not None:path.append(node)node = prev[node]path.reverse()return dist[end], path# 举个例子
graph = {'A': {'B': 3, 'C': 6},'B': {'C': 2, 'D': 1},'C': {'D': 1},'D': {}}
length, path = longest_path(graph, 'A', 'D')
print(f"最长路径为{path},路径长度(权重)为{length}")运行结果:

有向图:
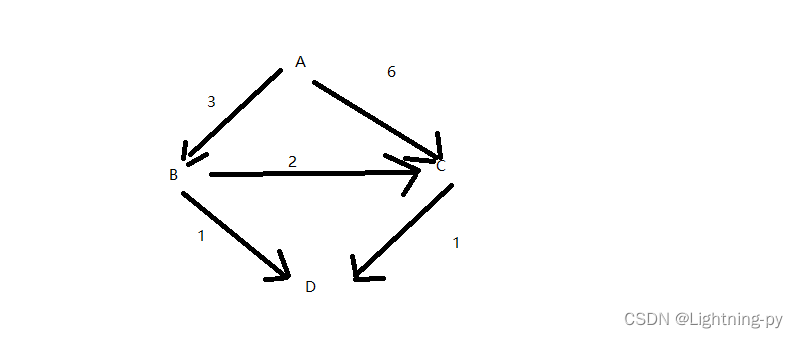
这个例子中,我们先使用topological_sort函数对有向图进行拓扑排序,然后依次计算每个节点的最长路径和路径终点,并使用prev字典记录每个节点在最长路径上的前驱节点。最后,我们生成从起点到终点的最长路径。这个算法的时间复杂度为O(V+E),其中V是节点数量,E是边数量。