图像简单运算

图像运算是以图像为单位对图像进行数学操作，运算对象以像素点为基本单位，运算结果为一幅灰度分布与原图像不同的新图像。

算术运算与逻辑运算

算术运算与逻辑运算中每次只涉及一个空间像素的位置，所以可以”原地操作“（在（x,y)位置做一个算术运算或逻辑运算的结果可以存在其中一个图像的相应位置，因为那个位置在其后运算中不会再使用）。两幅图像f(x,y)和h(x,y)算术或逻辑运算结果是g(x,y),可直接将g(x,y)覆盖f(x,y)或h(x,y)。

import matplotlib.font_manager as fm
from skimage import io
from matplotlib import pyplot as pltim1 = io.imread("K.png")
im2 = io.imread("Q.png")
f1 = fm.FontProperties('simhei', size=12)  # 设置字体
im_minus = im1 - im2
im_plus = im1 + im2plt.subplot(1, 4, 1)
plt.title('替身使者', fontproperties=f1)
plt.imshow(im1)plt.subplot(1, 4, 2)
plt.title('替身', fontproperties=f1)
plt.imshow(im2)
plt.subplot(1, 4, 3)
plt.title('相减', fontproperties=f1)
plt.imshow(im_minus)
plt.subplot(1, 4, 4)
plt.title('相加', fontproperties=f1)
plt.imshow(im_plus)plt.show()

为了方便演示这里选取了相同像素属性的图片，长宽相同。

点运算

点运算只涉及一幅原图像，运算对象是输入图像像素的灰度值。点运算也称灰度变换，且不会改变图像内空间的关系。若输入图像为A(x,y),输出图像为B(x,y)表示。点运算可表示B(x,y)=TA(x,y)。

点运算可分为线性点运算和非线性点运算。线性点运算原值和目标值通过线性方程来完成转换（灰度调整，图像反色）。非线性点运算对应非线性映射函数（灰度幂次变换，灰度对数变换等）

幂次变换又称伽马变换，数学形式： $t=c*s^{\gamma }$ ,其中c和 $\gamma$ 是常数，s代表图像像数值，t代表变换后的像素值。 $\gamma$ <1提高灰度级，正比函数上方，使图像变亮， $\gamma$ >1降低灰度级，正比函数下方，图像变暗。c=1，不同 $\gamma$ 值对应幂次变换函数如图。

skimage的exposure模块中包含幂次变换的函数adjust_gamma,可以对图像进行幂次变换。

from skimage import io,exposure
from matplotlib import pyplot as plt
#读入图像
img=io.imread("Jo.jpg")
#计算gamma不同值时的图像
img1=exposure.adjust_gamma(img,0.2)
img2=exposure.adjust_gamma(img,0.67)
img3=exposure.adjust_gamma(img,25)
plt.subplot(2,2,1)
plt.title('gamma=1')
plt.imshow(img)
plt.subplot(2,2,2)
plt.title('gamma=0.2')
plt.imshow(img1)
plt.subplot(2,2,3)
plt.title('gamma=0.67')
plt.imshow(img2)
plt.subplot(2,2,4)
plt.title('gamma=25')
plt.imshow(img3)
plt.show()

图像直方图

在统计学中，直方图（histogram）是一种对数据分布情况的图形表示，是一种二维统计图表，它的两个坐标分别是统计样本和该样本对应的某个属性的度量，以长条图（bar）的形式具体表现。因为直方图的长度及宽度很适合用来表现数量上的变化，所以较容易解读差异小的数值。

直方图是品质管理七大工具之一。

颜色直方图可分为：

全局颜色直方图：反映的是图像中颜色的组成分布，即出现了哪些颜色以及各种颜色出现的概率，Swain 和 Ballard最先提出了使用颜色直方图作为图像颜色特征的表示方法。他们还指出:颜色直方图相对于图像的以观察轴为轴心的旋转以及幅度不大的平移和缩放等几何变换是不敏感的，颜色直方图对于图像质量的变化(如模糊)也不甚敏感。颜色直方图的这种特性使得它比较适合于检索图像的全局颜色相似性的场合，即通过比较颜色直方图的差异来衡量两幅图像在颜色全局分布上的差异。

累加颜色直方图：当图像中的特征并不能取遍所有可取值时，统计直方图中会出现一些零值。这些零值的出现会对相似性度量的计算带来影响，从而使得相似性度量并不能正确反映图像之间的颜色差别。为解决这个问题，在全局直方图的基础上，Stricker和Orengo进一步提出了使用“累加颜色直方图”的概念。在累加直方图中，相邻颜色在频数上是相关的。相比一般直方图，虽然累加直方图的存储量和计算量有很小的增加，但是累加直方图消除了一般直方图中常见的零值，也克服了一般直方图量化过细过粗检索效果都会下降的缺陷。

主色调直方图：一幅图像中，往往少数几种颜色就涵盖了图像的大多数像素，而且不同颜色在图像中出现概率不同，可以通过统计图像中各种颜色出现的概率选出最频繁出现的几种颜色作为主色。使用主色并不会降低颜色匹配的效果，因为颜色直方图出现频率低的颜色往往不是图像主要内容，从某种程度而言，是对图像内容表示的一种噪声。

from skimage import io,exposure
from matplotlib import pyplot as plt
#读入图像
img=io.imread("Jo.jpg")
hist_r=exposure.histogram(img[:,:,0],nbins=256)
hist_g=exposure.histogram(img[:,:,1],nbins=256)
hist_b=exposure.histogram(img[:,:,2],nbins=256)

使用histogram()计算直方图。

计算颜色直方图需要将颜色空间划分为若干小的颜色区间，每个小区间能成为直方图的一个bin。这个过程称为颜色量化。计算颜色落在每个小区间内像素数量可以得到颜色直方图。设一幅彩色图像包含N个像素，像素的颜色被量化成L种不同颜色:

$H={h[1],h[2],.....h[L]}$

$h[k]=n_{k}/N$

$n_{k}$ 表示第k种颜色对应像素数量

直方图图像处理常见应用包括：直方图均衡化，直方图拉伸，以及直方图匹配。

直方图均衡化：

from skimage import exposure, io,data
import matplotlib.pyplot as pltimg=data.moon()
plt.figure("hist", figsize=(8, 8))
arr = img.flatten()
plt.subplot(221)
plt.imshow(img, plt.cm.gray)
plt.subplot(222)
plt.hist(arr, bins=256,edgecolor='None',facecolor='red')
img1 = exposure.equalize_hist(img)  # 原始图像直方图
arr1 = img1.flatten()
plt.subplot(223)
plt.imshow(img1, plt.cm.gray)
plt.subplot(224)
plt.hist(arr1, bins=256,edgecolor='None',facecolor='red')
plt.show()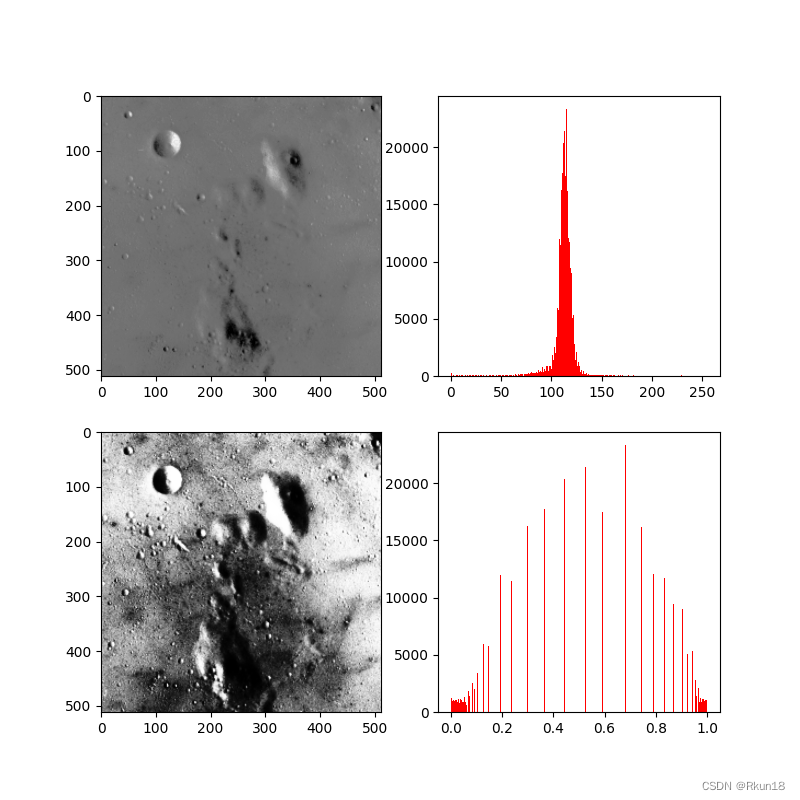

均衡化后图像更容易进行目标分辨.

图像卷积

图像卷积操作就是图像空间域滤波的基础运算，就是循环将图像和卷积核逐个元素相乘再求和，得到的卷积后图像过程。

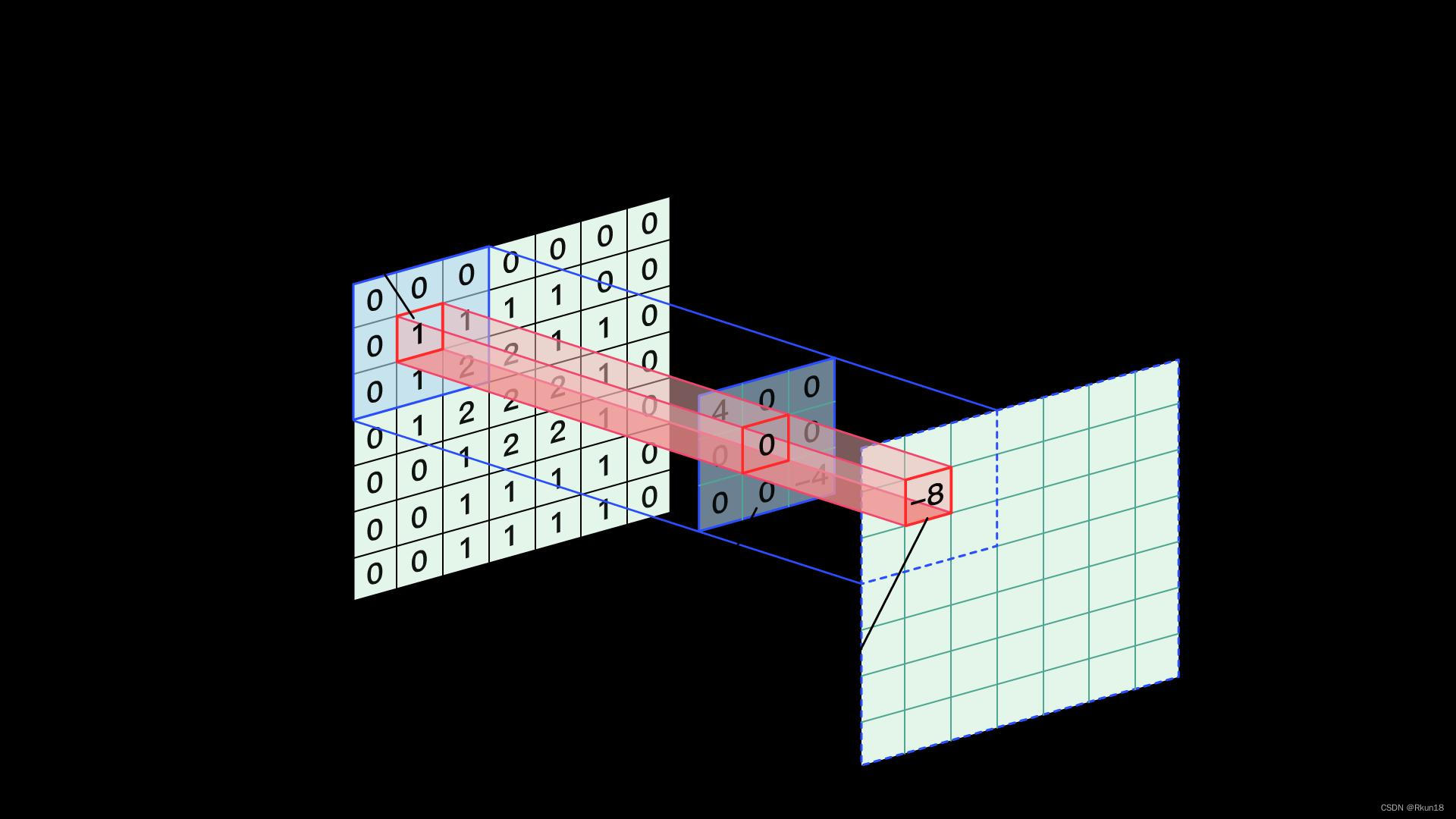
假设卷积核使用K表示，大小为（m*n）；原始图像表示为S,大小为(M*N)，结果图像表示T

$T(x,y)=\sum_{i=-a}^{a}\sum_{j=-b}^{b}K(i,j)*S(x+i,y+j)$

m=2*a+1,n=2*b+1

卷积操作中，卷积核在原始图像中从上到下，从左到右滑动扫描，每次扫描使用卷积核与扫描覆盖区域图像做一次卷积运算，然后在移动到下一个位置进行扫描，直到扫描完毕。

import numpy as np
from skimage import io, datadef mat_conv(arr, kernel):  # 数组和卷积核n = len(kernel)ans = 0for i in range(n):for j in range(n):ans += arr[i, j] * float(kernel[i, j])return ansdef conv_2d(img, kernel):n = len(kernel)img1 = np.zeros((img.shape[0] + 2 * (n - 1), img.shape[1] + 2 * (n - 1)))img1[(n - 1):(n + img.shape[0] - 1), (n - 1):(n + img.shape[1] - 1)] = imgimg2 = np.zeros((img1.shape[0] - n + 1, img1.shape[1] - n + 1))for i in range(img1.shape[0] - n + 1):for j in range(img1.shape[1] - n + 1):tmp = img1[i:i + n, j:j + n]img2[i, j] = mat_conv(tmp, kernel)new_img = img2[(n - 1):(n + img.shape[0] - 1), (n - 1):(n + img.shape[1] - 1)]return new_imgkernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype=int)
img = data.moon()
io.imshow(img)
io.show()
new = conv_2d(img, kernel)
io.imshow(new)
io.show()

原图：

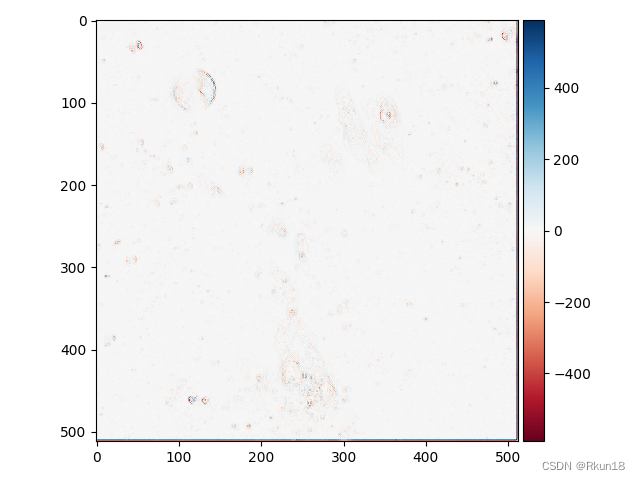
卷积后：

灰度反转

from skimage import iodef my_gray(img):img = 255 - imgreturn imgim1 = io.imread("P1.jpg")
io.imshow(im1)
io.show()
im2 = my_gray(im1)
io.imshow(im2)
io.show()