数据结构中常见的树

二叉树：每个子节点只有两个节点的树，每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结
点)，并且，二叉树的子树有左右之分，其次序不能任意颠倒
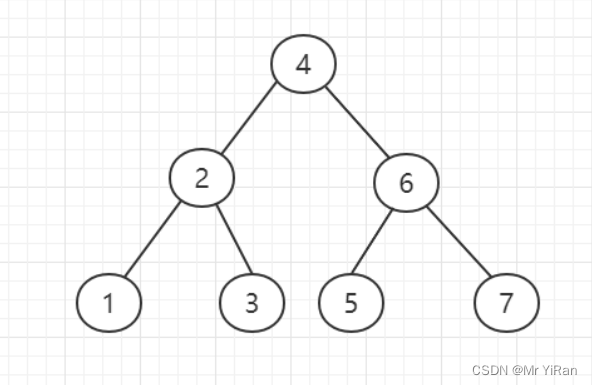
在这里插入图片描述
我们一般在解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树。

满二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的节点，并且度为0的节点在同一层上，则这棵二叉树为满二叉树。
如图所示：
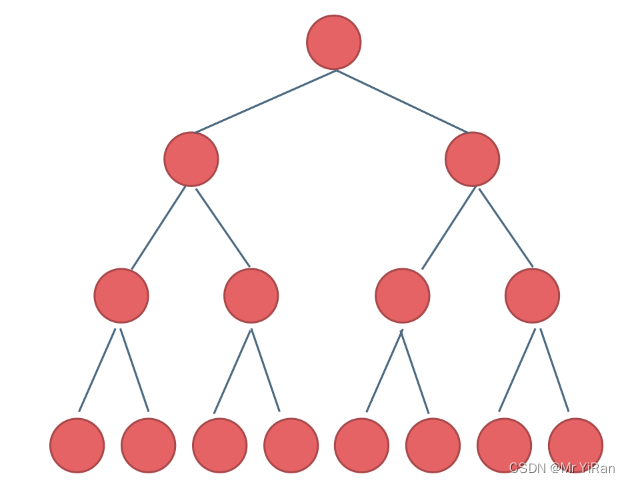
在这里插入图片描述
这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

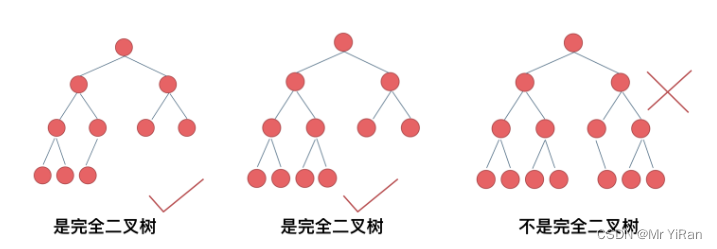
完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。
在这里插入图片描述

二叉树遍历操作

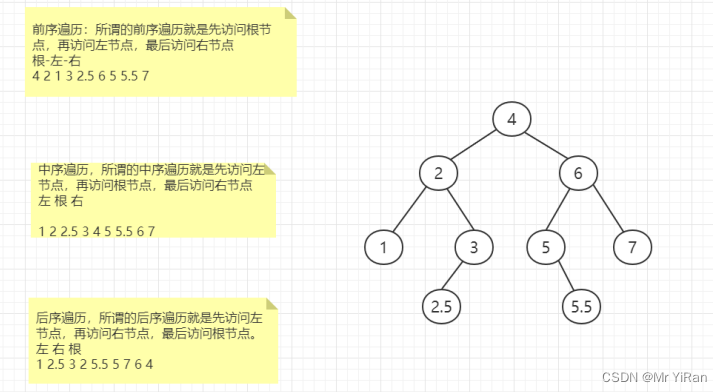
二叉树中的遍历规则有如下三种：
前序遍历：所谓的前序遍历就是先访问根节点，再访问左节点，最后访问右节点，即根-左-右遍历(前序)
中序遍历：所谓的中序遍历就是先访问左节点，再访问根节点，最后访问右节点，即左-根-右遍历
后序遍历：所谓的后序遍历就是先访问左节点，再访问右节点，最后访问根节点。即左-右-根遍
在这里插入图片描述
查找最小值：沿着根节点的左子树一路查找，直到最后一个不为空的节点，该节点就是当前这个树的最
小节点
查找最大值：沿着根节点的右子树一路查找，直到最后一个不为空的节点，该节点就是当前这个树的最
大节点
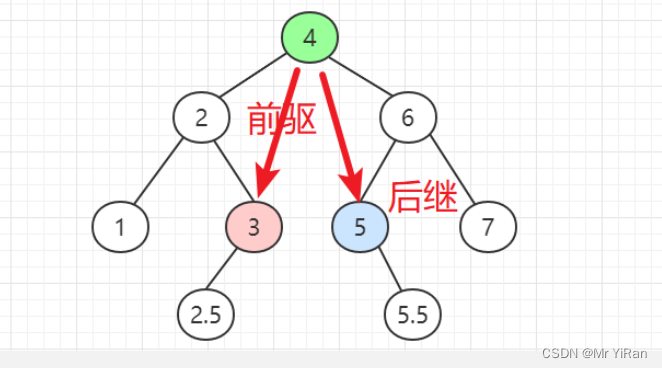
查找前驱节点：小于当前节点的最大值
查找后继节点：大于当前节点的最小值
在这里插入图片描述
删除节点
二叉树中的删除节点：本质上是找前驱节点或者后继节点来替代

叶子节点直接删除
只有一个子节点的用子节点替代(本质上就是找的前驱节点或者后继节点，左节点就是前驱节点，右
节点就是后继节点)
有两个子节点的，需要找到替代节点(替代节点就是前驱节点或者后继节点）

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树
下面这两棵树都是搜索树

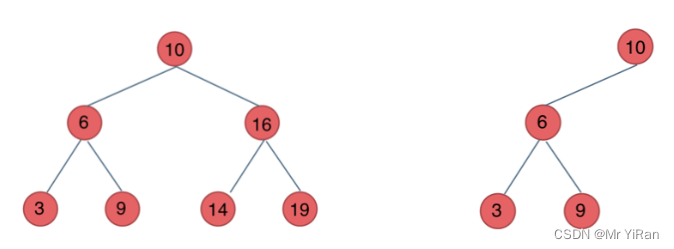
但是一个二叉搜索树是由n个节点随机构成,所以，对于某些情况,二叉搜索树会退化成一个有n个节点的线
性链.如下图

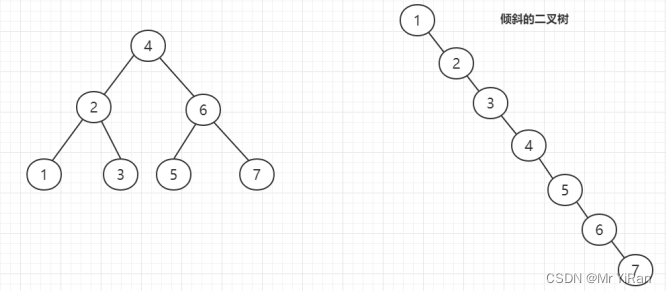
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
如图：
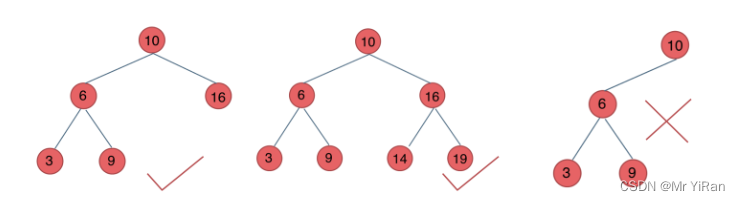
在这里插入图片描述
最后一棵不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

2-3-4树

2-3-4树是四阶的 B树(Balance Tree)，他属于一种多路查找树，它的结构有以下限制：
所有叶子节点都拥有相同的深度。
节点只能是 2-节点、3-节点、4-节点之一。

2-节点：包含1个元素的节点，有2个子节点
3-节点：包含2个元素的节点，有3个子节点
4-节点：包含3个元素的节点，有4个子节点

所有节点必须至少包含1个元素
元素始终保持排序顺序，整体上保持二叉查找树的性质，即父结点大于左子结点，小于右子结点；
而且结点有多个元素时，每个元素必须大于它左边的和它的左子树中元素。
如图所示：
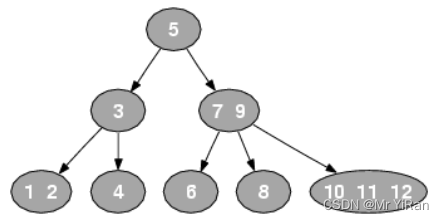
在这里插入图片描述
2-3-4树的查询操作像普通的二叉搜索树一样，非常简单，但由于其结点元素数不确定，在一些编程
语言中实现起来并不方便，实现一般使用它的等同——红黑树

2-3-4树生成过程

第一次插入—2节点
在这里插入图片描述
插入第二个节点–3节点合并

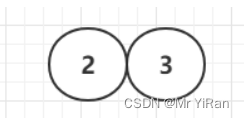
在这里插入图片描述
插入第三个节点—4节点合并

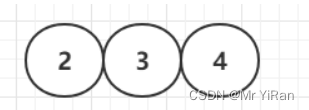
插入第4个节点—需要分裂

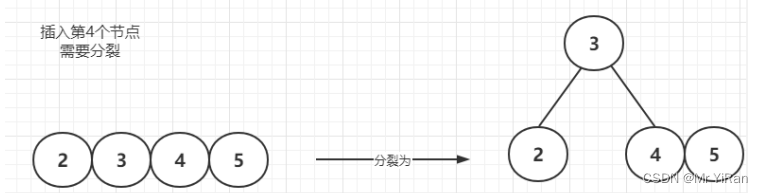
插入6

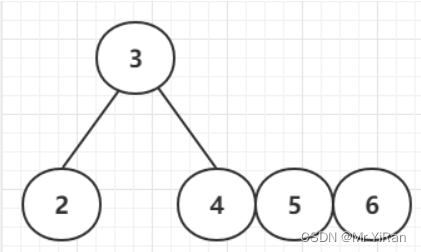
插入7

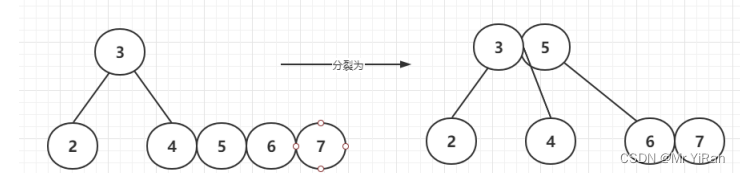
插入8

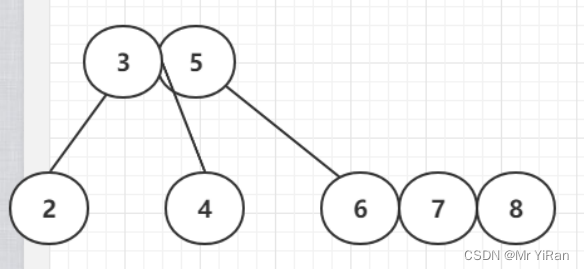
插入9

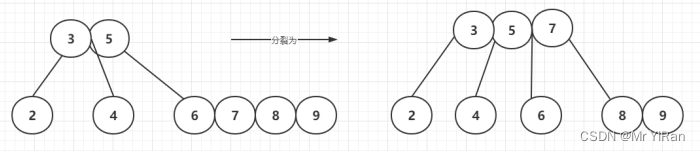
插入10

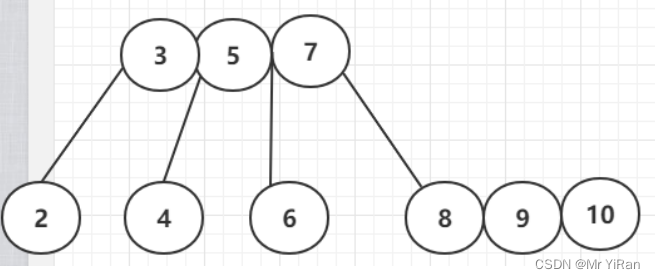
插入11
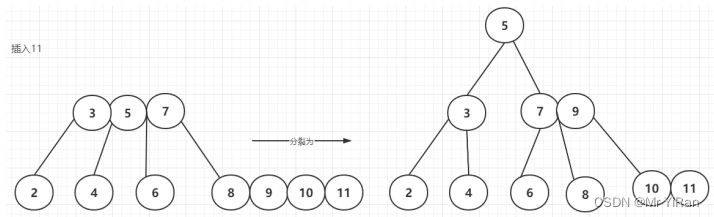
在这里插入图片描述

插入12
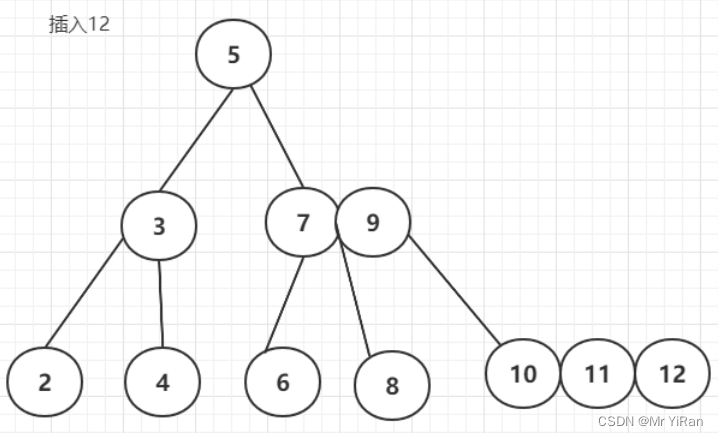
在这里插入图片描述
最后插入1

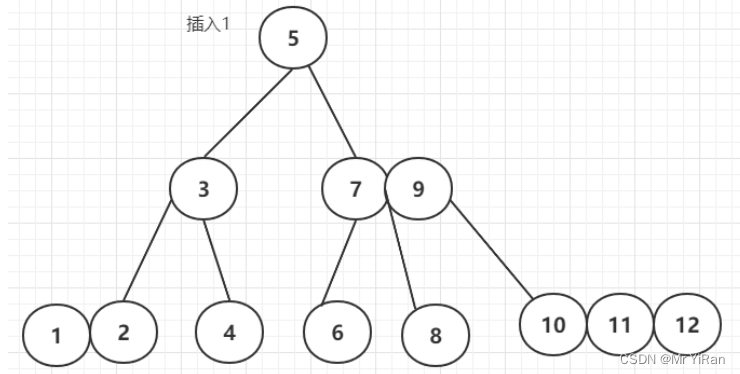
和红黑树的等价关系

红黑树起源于2-3-4树，它的本质就是2-3-4树。
2节点
一个2节点对应的红黑树节点就是一个黑色节点
在这里插入图片描述
3节点
一个三节点可以有两种情况的红黑树节点，一种是右倾，一种是左倾，所以一个2-3-4树可以有多个红黑
树

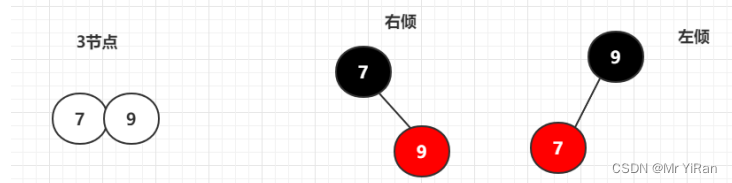
原则上黑下红
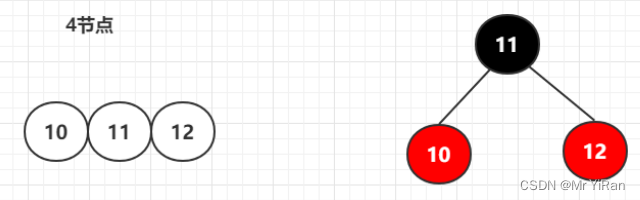
4节点
一个四节点转换的情况只有一种，中间节点黑色，左右节点红色

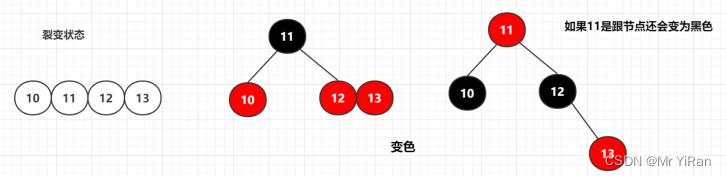
裂变状态
还有就是在2-3-4树中存在的裂变状态。转换为红黑树后会先变色(不能有两个相邻的红色节点)
在这里插入图片描述

转换为红黑树

2-3-4树是如何转换为对应的红黑树的?
原始的2-3-4树
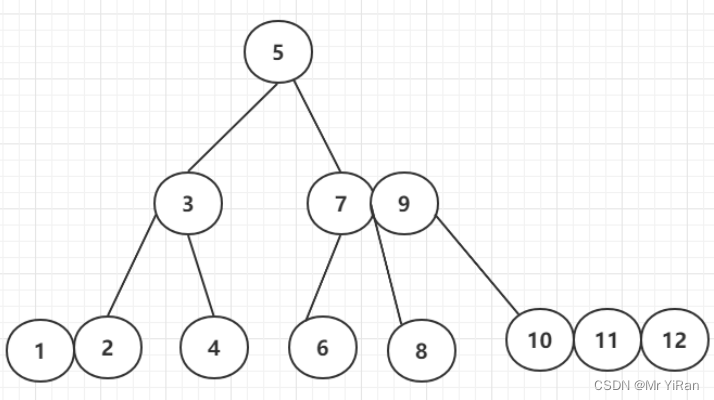
在这里插入图片描述
按照右倾规则来转换为

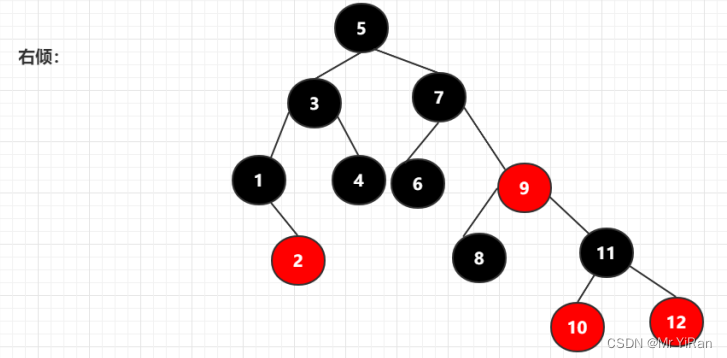
转换后满足黑色节点平衡的要求

按照左倾规则来转换为
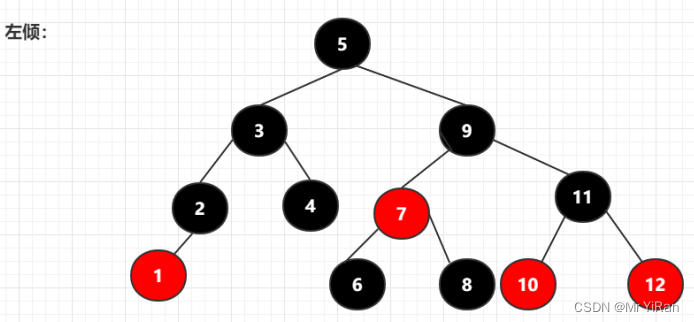
在这里插入图片描述

红黑树

红黑树，Red-Black Tree 「RBT」是一个自平衡(不是绝对的平衡)的二叉查找树(BST)，树上的每个节点
都遵循下面的规则：

每个节点要么是黑色，要么是红色。
根节点是黑色。
每个叶子节点（NIL）是黑色。
每个红色结点的两个子结点一定都是黑色。
任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

红黑树能自平衡，它靠的是什么？三种操作：左旋、右旋和变色

操作	描述
左旋	以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。
右旋	以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。
变色	结点的颜色由红变黑或由黑变红

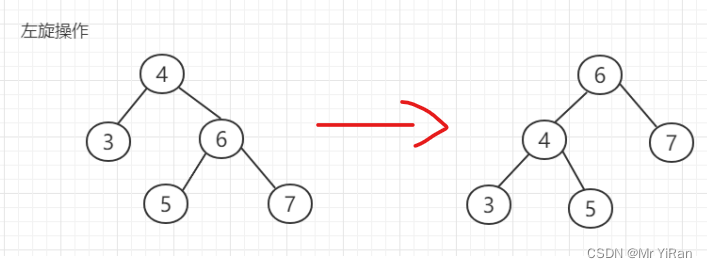
旋转操作

左旋：以某个节点作为旋转点，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，左子节点保持不变。
在这里插入图片描述
右旋：以某个节点作为旋转点，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。

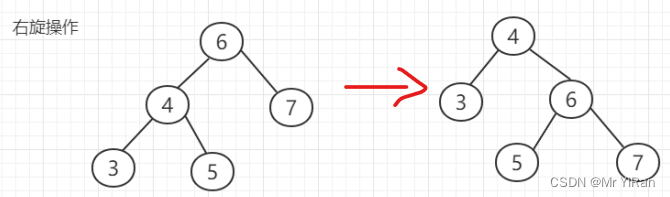
代码实现：
类结构定义

public class BRTree {private static final boolean RED = false;private static final boolean BLACK = true;private RBNode root;public RBNode getRoot() {return root;}public void setRoot(RBNode root) {this.root = root;}/*** 表示 节点* @param <K>* @param <V>*/static class RBNode<K extends Comparable<K>,V>{// 节点是双向的private RBNode parent;private RBNode left;private RBNode right;private boolean color;private K key;private V value;public RBNode() {}public RBNode(RBNode parent, RBNode left, RBNode right, boolean color, Kkey, V value) {this.parent = parent;this.left = left;this.right = right;this.color = color;this.key = key;this.value = value;}public RBNode getParent() {return parent;}public void setParent(RBNode parent) {this.parent = parent;}public RBNode getLeft() {return left;}public void setLeft(RBNode left) {this.left = left;}public RBNode getRight() {return right;}public void setRight(RBNode right) {this.right = right;}public boolean isColor() {return color;}public void setColor(boolean color) {this.color = color;}public K getKey() {return key;}public void setKey(K key) {this.key = key;}public V getValue() {return value;}public void setValue(V value) {this.value = value;}}
}

左旋代码实现

  /*** 实现左旋* p                 pr* / \               / \* pl  pr     ==>   p   rr* / \             / \* rl rr          pl  rl* 左旋操作：* p-pl 和pr -rr的关系不需要调整* 需要调整的情况* 1.pr-rl 调整为 p-rl* 将rl变为p的右子节点* 将p设置为rl的父节点* 2. 判断p是否右父节点* 有：* pr.parent=p.parent* pr为p.parent的子节点，到底是左子节点还是右子节点呢？* if(p.parent.left==p)* p.parent.left=pr* else{* P.parent.right=r* }* 没有：* 直接把pr设置为root节点* 3.最后p和pr交换* p.parent=pr* pr.left=p** @param p*/private void leftRotate(RBNode p) {if (p != null) {//获取到了pr节点RBNode pr = p.right;//情况1：pr-rl调整为p-rlp.right = pr.left;if (pr.left != null) {pr.left.parent = p;}//情况2：判断P节点是否有父节点pr.parent = p.parent;//不管是否存在父节点，我们都设置P的父节点也为pr的父节点if (p.parent == null) {//说明P就是root节点，这时pr会变成新的root节点root = pr;} else if (p.parent.left == p) {   //说明p存在父节点//说明p是父节点的左子节点，那么pr也肯定是p的父节点的左子节点p.parent.left = pr;} else {p.parent.right = pr;}//情况3：设置p为pr的左子节点pr.left = p;p.parent = pr;}}

右旋代码实现

 private void rightRotate(RBNode p) {if (p != null) {//获取到了pr节点RBNode pr = p.left;//情况1：pr-rl调整为p-rlp.left = pr.right;if (pr.right != null) {pr.right.parent = p;}//情况2：判断P节点是否有父节点pr.parent = p.parent;//不管是否存在父节点，我们都设置P的父节点也为pr的父节点if (p.parent == null) {//说明P就是root节点，这时pr会变成新的root节点root = pr;} else if (p.parent.left == p) {   //说明p存在父节点//说明p是父节点的左子节点，那么pr也肯定是p的父节点的左子节点p.parent.left = pr;} else {p.parent.right = pr;}//情况3：设置p为pr的左子节点pr.right = p;p.parent = pr;}}