继续咱们百家稷学专题,本次是有三AI在珠海格力电器进行的深度学习技术培训,百家稷学的目标,是走进100所高校和企业进行学习和分享。
分享主题
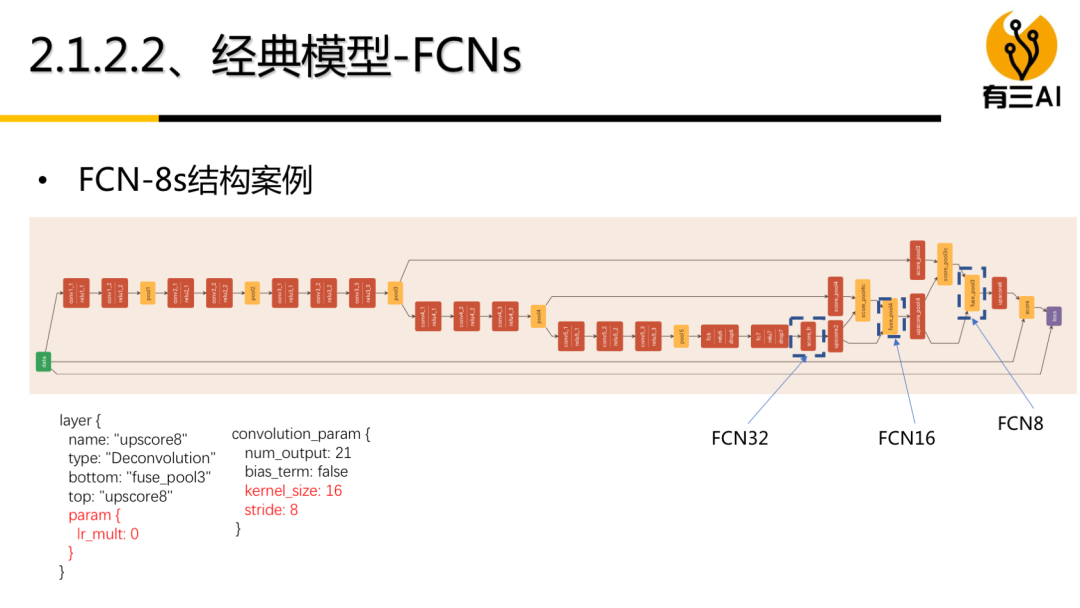
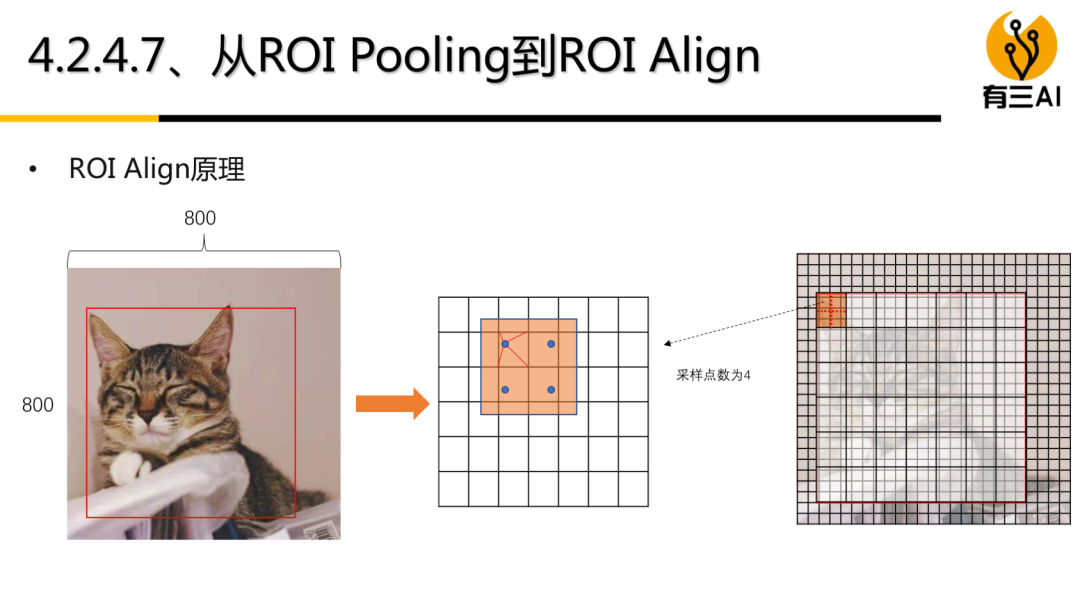
本次分享是在珠海格力电器,主题为《计算机视觉与深度学习典型实践》,分享人言有三。内容以目标检测,图像分割,生成对抗网络为主,PPT超过180页。







配套资料下载
本次非公开技术分享,因此不对外提供技术资料下载。大家可以关注其他《百家稷学》的内容,一些分享如下:
【百家稷学】深度学习计算机视觉生产实习(山西农业大学暑期实训)
【百家稷学】深度学习原理及其应用(南京财经大学与上海交通大学技术分享)
【百家稷学】卷积神经网络的前世、今生与未来(武汉工程大学技术分享)
【百家稷学】从传统方法到深度学习,人脸算法和应用的演变(河南平顶山学院技术分享)
【百家稷学】基于华为NAIE与Mindspore的视觉实训(东莞华为松山湖研究所实训)
转载文章请后台联系
侵权必究



往期精选
【总结】有三AI视觉算法工程师成长指导手册不更新了?不,换视频更新了!
【CV春季划】2021年有三AI-CV春季划出炉,最后一届言有三手把手从零带学
【CV夏季划】告别入门,提升眼界,从掌握最有价值的那些CV方向开始
【CV秋季划】生成对抗网络GAN有哪些研究和应用,如何循序渐进地学习好?
【CV秋季划】模型优化很重要,如何循序渐进地学习好?
【CV秋季划】人脸算法那么多,如何循序渐进地学习好?
【CV秋季划】图像质量提升与编辑有哪些研究和应用,如何循序渐进地学习好?