一、题目

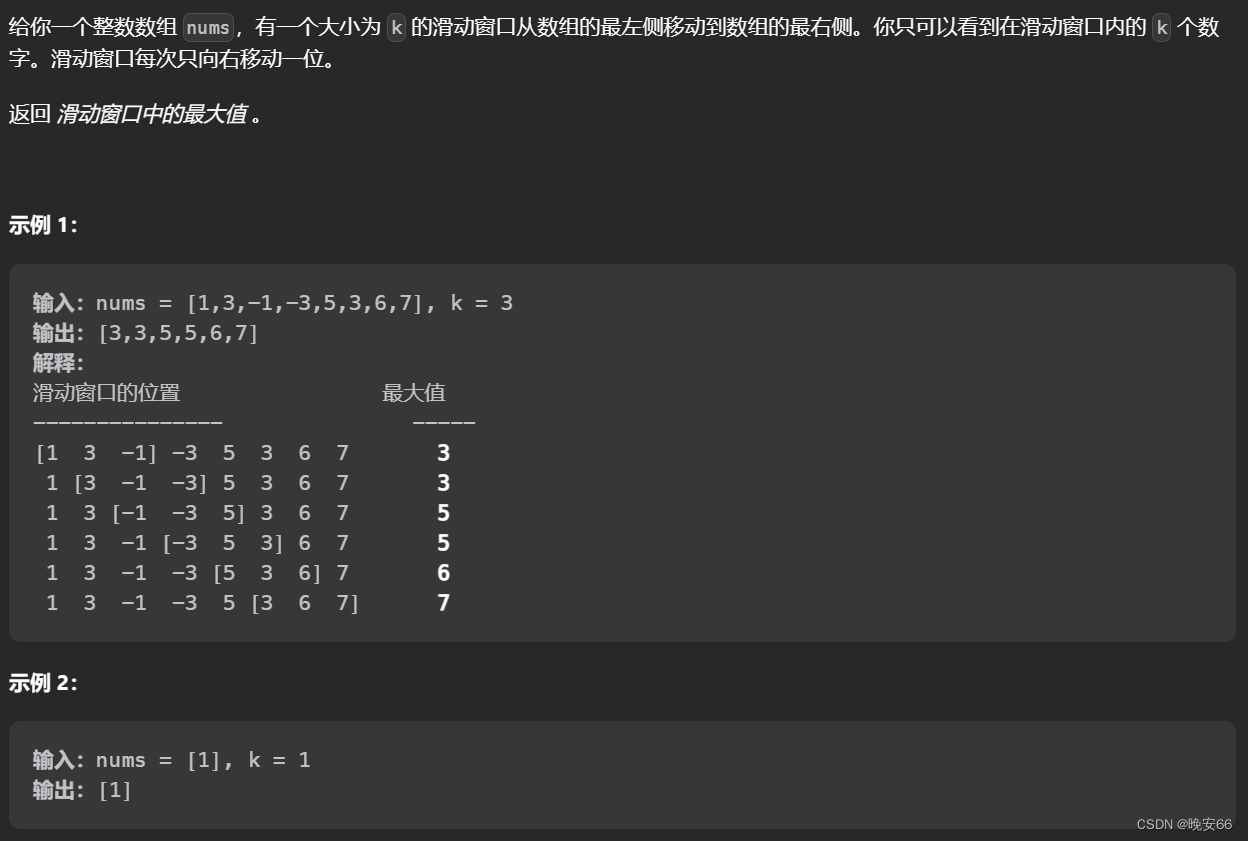
在这里插入图片描述

二、解法

思路分析：这道题我们如果用暴力破解法需要 $O (n * k)$ 的复杂度。思索再三，我们需要一个能够把最大值放在队头，整个队列单调递减的单调队列。每次窗口移动的时候，调用que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后que.front()就返回我们要的最大值。要注意两点：1、最大值必须在队头，这样我们才能用que.front()访问 2、队头的最大值元素必须在滑动窗口内部，否则就不是滑动窗口的最大值。

对于上面两个问题我们分别在pop和push中做这样的逻辑：1、如果队尾元素如果小于入队元素，就弹出队尾元素，直到入队元素大于等于队尾元素才插入入队元素 2、每次访问que.front()之前，都进行一次判断，如果队头的最大值和nums[i-k]进行对比，如果相等，说明这个最大值元素不在滑动窗口中（滑动窗口范围为i-k+1,…,i-1,i）。
程序如下：

class MyQueue {	// 单调队列，递减
public:deque<int> que;		// deque为双向数组，这里用它当做单调队列的底层实现void pop(int value) {	if (!que.empty() && value == que.front())	// 如果元素相等则弹出，否则不做操作que.pop_front();}void push(int value) {	// 保证队头元素一定是最大的while (!que.empty() && value > que.back()) {	// 队尾元素如果小于入队元素，就弹出队尾元素que.pop_back();}que.push_back(value);	// 直到入队元素大于等于队尾元素，插入}int front() {return que.front();}
};class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue que;	// 单调队列vector<int> result;for (int i = 0; i < k; ++i) {que.push(nums[i]);}result.push_back(que.front());for (int i = k; i < nums.size(); ++i) {que.pop(nums[i - k]);	// 弹出队头的元素，防止最大值一直在队头，且这个最大值又不在滑动窗口中的情况que.push(nums[i]);result.push_back(que.front());}return result;}
};

复杂度分析：

时间复杂度： $O (n)$ ，所有元素的push和pop操作都只进行一次。
空间复杂度： $O (k)$ ，需要一个大小为k的单调队列额外空间。

三、完整代码

# include <iostream>
# include <vector>
# include <deque>
using namespace std;class MyQueue {	// 单调队列，递减
public:deque<int> que;		// deque为双向数组，这里用它当做单调队列的底层实现void pop(int value) {	if (!que.empty() && value == que.front())	// 如果元素相等则弹出，否则不做操作que.pop_front();}void push(int value) {	// 保证队头元素一定是最大的while (!que.empty() && value > que.back()) {	// 队尾元素如果小于入队元素，就弹出队尾元素que.pop_back();}que.push_back(value);	// 直到入队元素大于等于队尾元素，插入}int front() {return que.front();}
};class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue que;	// 单调队列vector<int> result;for (int i = 0; i < k; ++i) {que.push(nums[i]);}result.push_back(que.front());for (int i = k; i < nums.size(); ++i) {que.pop(nums[i - k]);	// 弹出队头的元素，防止最大值一直在队头，且这个最大值又不在滑动窗口中的情况que.push(nums[i]);result.push_back(que.front());}return result;}
};void my_print(vector <int>& v, string msg)
{cout << msg << endl;for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {cout << *it << "  ";}cout << endl;
}void VectorGenerator(int* arr, vector<int>& v, int arr_len) {for (int i = 0; i < arr_len; ++i) {v.push_back(arr[i]);}
}int main()
{int window_size = 3;int arr[] = {1, 3, -1, -3, 5, 3, 6, 7};int arr_len = sizeof(arr) / sizeof(int);vector<int> nums;VectorGenerator(arr, nums, arr_len);my_print(nums, "目标数组");Solution s1;vector<int> result = s1.maxSlidingWindow(nums, window_size);my_print(result, "滑动窗口最大值");system("pause");return 0;
}