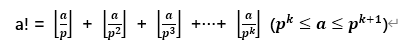四、数学知识

1、分解质因数

1、目标：把一个整数分解成若干质数，输出每个质数以及它的次数。

2、思路：首先判定一个数是否是质数，即用大于等于2的因数去试除，如果余零则说明不是质数，则用该因数累除直到余数不为零，同时创建一个变量来记录次数（幂）。总之，是基于试除法判定因数的。

3、代码注意点：

（1）1 到 n 中最多只包含一个大于 $\sqrt{n}$ 的质因子，所以不要忘记如果最后得到的数依然大于1的话要输出他和相应的次数

（2）试除法不推荐采用 i <= sqrt(n)因为每次循环都要执行一次，速度慢；也不推荐i * i <= n因为 i * i可能会溢出。试除法的时间复杂度是 $O(\sqrt{n})$

2、埃拉托斯特尼筛素数法 (sieve of Eratosthenes)

1、目标：筛选出从1 到 n之内的所有素数。

2、思路：依次把 1 到 n 之间的素数的倍数都筛出去。

3、时间复杂度：它的时间复杂度是 $O(nloglogn)$

3、线性筛素数法

1、目标：线性地筛出从 1 到 n之间的所有素数

2、思路：埃拉托斯特尼筛法中一些数会被重复地筛，比如6既是2的倍数又是3的倍数，所以会被筛两次，不是线性的。因此线性筛素数法的思想就是保证从 1 到 n 的每个合数都被它们最小的质数筛掉并且只筛一次。

3、代码注意点：

（1）在筛素数时，因为要把 prime[j] * i筛掉，所以循环的条件里应该是 prime[j] <= n / i
（2）和埃拉托斯特尼筛法的代码模板不同的是，在线性筛法中如果 st[j] = true则执行筛选的循环体，但是在埃拉托斯特尼筛法中当 st[j] = true时会进行 continue操作。st[i]存储的是 i 是否已经被筛掉了。

（3）在筛选循环体内应该最后判断 prime[ j ] 是否是 i 的最小质数，如果是则break。因为线性筛法正是要让每个合数都被它们的最小质数筛掉。如果提前break了，则只筛掉了小于 i 的最小质数的数的倍数。

4、约数的个数

1、目标：求一个正整数的约数（不是质因子）的个数

2、思路：一个正整数可以表示成：
$$\begin{gathered} N=P_1^{C_1}\cdot P_2^{C_2}\cdot P_3^{C_3}...\cdot P_n^{C_n} \\ {P}_i:质因子,C_i:质因子的次数 \end{gathered}$$
那么由于每一个质因子的次数可以取 $[0,C_i]$ 所以约数的个数显然是：
$$\sum _{i=0}^n(C_i+1)$$
3、代码注意点：

（1）最后的答案可能很大，最好用 long long 来存储。

（2）利用哈希表来存储约数和约数的个数会比较方便。

（3）res = res * (x.second + 1) % M;这一句话不能写成 res *= (x.second + 1) % M

5、约数之和

1、目标：求一个正整数的约数（不是质因子）的和

2、思路：一个正整数可以表示成
$$\begin{gathered} N=P_1^{C_1}\cdot P_2^{C_2}\cdot P_3^{C_3}...\cdot P_n^{C_n} \\ {P}_i:质因子,C_i:质因子的次数 \end{gathered}$$
那么由于每一个质因子的次数可以取 $[0,C_i]$ 所以，所有约数的和显然是：
$$\sum _{i=1}^{i=n}\sum _{j=0}^{j=n}{P}_i^j$$
3、代码注意点：

（1）${\sum }_{j=0}^{j=n}{P}_j$ 可以用一句话写出来：int t = 1; while(c--) t = (t * p + 1)

（2）同样这道题的答案也有可能爆int，所以用 long long 来存储。

6、欧几里得算法

1、目标：求一个正整数的最大公约数

2、思路：$gcd(a,b)=gcd(b,a\mathrm{m}\mathrm{o}\mathrm{d}b)$ 证明需要用到一些简单的性质。如果 $d|a,d|b\to d|(xa+yb)$
$$\begin{array}{rl}& \because a\mathrm{m}\mathrm{o}\mathrm{d}b=a-\lfloor \frac{a}{b}\rfloor \cdot b\\ & letc=\lfloor \frac{a}{b}\rfloor \\ & \therefore a\mathrm{m}\mathrm{o}\mathrm{d}b=a-c\cdot b\\ & \therefore ifgcd(b,a\mathrm{m}\mathrm{o}\mathrm{d}b)=t\\ & t|b,t|(a-c\cdot b)\\ & \therefore t|b,t|a\\ & \therefore gcd(b,a\mathrm{m}\mathrm{o}\mathrm{d}b)=gcd(a,b)\end{array}$$

7、欧拉 $\varphi$ 函数（Euler’s totient function）

1、目标：求 1 到 N 之间与 N 互质的数的个数

2、结论：
$$\begin{gathered} N=p_1^{a_1}{p}_2^{a_2}\dots p_m^{a_m} \\ \varphi (N)=N\ast \frac{p_1-1}{p_1}\ast \frac{p_2-1}{p_2}\ast \dots \ast \frac{p_m-1}{p_m} \end{gathered}$$
上式每一项都向下取整。

3、证明：可以利用容斥原理，大致思路是从 n 个数当中减去一个质数的倍数，则有些数可能同时是两个质数的公倍数，那么它们就被减去了两次，在把它们的数量加回来，再减去三个质数的公倍数，再加上四个质数的公倍数的个数……

4、代码注意点：

（1）需要写成res = res / i * (i - 1)，不能写成 res = res * (i - 1) / i防止溢出

8、线性筛法求欧拉 $\varphi$ 函数

1、目标：求出从 1 到 N之间每一个数的欧拉函数

2、思路：如果只是在普通的欧拉函数外面套一层循环，时间复杂度过高。所以想到借鉴线性筛素数法，能否线性地求出1到 N 的欧拉函数呢？首先，一个质数 P 的欧拉函数显然是 P - 1。接下来根据线性筛素数法的模板，需要根据 i % primes[j]是否等于0来分情况讨论 primes[j]*i 的欧拉函数是多少。

如果等于0，则说明 primes[ j ] 是 i 的一个质因子，因为 primes[j]*i 的欧拉函数只和它的质因子有关， primes[j]*i 的质因子比 i 的质因子多了一个 primes[ j ]，并且 primes[ j ] 还是一个质数，所以 primes[j]*i 的欧拉函数显然应该是：$primes[j]\cdot \varphi (i)$

如果不等于0，那么在计算 primes[j]*i 的欧拉函数时除了要再乘上一个 primes[ j ] 还要再乘一项 $1-\frac{1}{primes[j]}$ ，所以 primes[j]*i 的欧拉函数应该是：$(primes[j]-1)\cdot \varphi (i)$

综上，就可以线性地求得 1 到 N 之间每个数的欧拉函数。

9、快速幂

1、目标：快速地求出 $a^k\mathrm{m}\mathrm{o}\mathrm{d}p,1\le a,k,p\le 10^9$ 它的时间复杂度为 $O(logk)$

2、思路：首先预处理出来：
$$\begin{array}{rl}& a^{2^0}\mathrm{m}\mathrm{o}\mathrm{d}p\\ & a^{2^1}\mathrm{m}\mathrm{o}\mathrm{d}p\\ & a^{2^2}\mathrm{m}\mathrm{o}\mathrm{d}p\\ & ⋮\\ & a^{2^{logk}}\mathrm{m}\mathrm{o}\mathrm{d}p\end{array}$$
然后把 $a^k$ 组合出来，$a^k=a^{2^{x_1}}\cdot a^{2^{x_2}}\cdot a^{2^{x_3}}\cdots \cdot a^{2^{x_k}}$ ，显然实质上就是要让：$k=2^{x_1}+2^{x_2}+\cdots +2^{x_k}$ ，要达到这种目标只需要把 k 转换成二进制表示就行了。

预处理这一步可以采用反复平方法。

10、求逆元

1、目标：找到一个整数 $x$ 使得 $\frac{a}{b}\equiv a\cdot x(modm)$ ，其中 $b$ 和 $m$ 互质。记 $x=b^{-1}$，这么做的好处是可以把除法转换成乘法。对该式子稍作变形即可得到：$b\cdot x\equiv 1(modm)$，这个式子较为简单可以用来方便地求逆元。

2、欧拉定理与费马小定理：

• 欧拉定理：当 $n$ 和 $a$ 互质时：

$$a^{\phi (n)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}n)$$

提供一种证明思路：

已知 $\varphi (n)$ 的含义是 1 到 n 中和 n 互质的个数。假设这些数是 $x_1,x_2,\cdots ,x_{\varphi (n)}$ ，因为 $a$ 又和 $n$ 互质所以 $a{x}_1,a{x}_2,\cdots ,a_{x_{\varphi (n)}}$ 也和 $n$ 互质。所以 $x_1,x_2,\cdots ,x_{\varphi (n)}$ 和 $a{x}_1,a{x}_2,\cdots ,a_{x_{\varphi (n)}}$ 其实是同一堆数，所以应该有：
$$
\begin{aligned}
&x_1x_2\cdots x_{\phi(n)} \equiv ax_1ax_2\cdots ax_{x_{\phi(n)}} \ \ (mod \ \ n)\
&x_1x_2\cdots x_{\phi(n)} \equiv a^{\phi(n)}x_1x_2\cdots x_{x_{\phi(n)}} \ \ (mod \ \ n)\
&\because
\left{
\begin{array}{lr}
x \equiv y \ \ (mod \ \ t)\
x\cdot z \equiv y \ \ (mod \ \ t)
\end{array}
\right.

\to

z \equiv 1 \ \ (mod \ \ t)\

&\therefore
a^{\phi(n)} \equiv 1 \ \ (mod \ \ n)
\end{aligned}
$$

• 费马小定理：当 $n$ 是质数时，不妨设 $n=p$ 则有 $\varphi (p)=p-1$，则有：
  $$a^{p-1}\equiv 1(modp)$$

3、逆元求解思路：$b\cdot x\equiv 1(modm)$ ，当 $m$ 是质数时，根据费马小定理有：$b^{m-1}\equiv 1(modm)$ ，进一步可以得到：
$$b\cdot b^{p-2}\equiv 1(modm)$$
所以得到一个结论：$b$ 存在乘法逆元的充要条件是 $b$ 与模数 $m$ 互质。当模数 $m$ 为质数时，$b^{m-2}$ 即为 $b$ 的乘法逆元。

所以，当 $m$ 为质数时，要求 $b$ 模 $m$ 的逆元只要求 $b^{m-2}(modm)$ 即可，此时问题就转化为了快速幂！

当 $m$ 不是质数时，可以用扩展欧几里得方法解一个线性同余方程：$ax\equiv 1(modm)$

4、代码注意点：

（1）所有模数的倍数都不存在逆元

11、扩展欧几里得算法

1、裴蜀定理：对 $\forall a,b\in Z,\exists x,y\in Zs.t.ax+by=gcd(a,b)$

2、目标：对给出的一对 $(a,b)$ 求出符合裴蜀定理的 $(x,y)$

3、思路：在欧几里得算法的基础上加以改进。

首先当 $b=0$ 时，$gcd(a,b)=a$ 所以显然 $x=1,y=0$ 可以是一组解；

当 $b\ne 0$ 时，则变成了 $d=gcd(b,amodb)$ ，又 $amodb=a-\lfloor \frac{a}{b}\rfloor \cdot b$ ，所以需要求：
$$\begin{array}{rl}& yb+x(a-\lfloor \frac{a}{b}\rfloor \cdot b)=d\\ & xa+(y-\lfloor \frac{a}{b}\rfloor \cdot x)b=d\end{array}$$
与最初的等式：$xa+yb=d$ 相比，$a$ 的系数不用更新，$y$ 的系数进行更新即可。

4、代码注意点：

（1）迭代的时候，对调 $x,y$ 的位置可以方便计算。

12、线性同余方程

1、目标：求解形如：$ax\equiv b(modm)$ 的方程，其中 $x$ 是未知数。

2、思路：将方程变形后可以用扩展欧几里得法求解。原式可变为：
$$\begin{gathered} ax=ym+b \\ ax-ym=b \\ lety\prime =-y, \\ ax+my\prime =b \end{gathered}$$
根据裴蜀定理，当且仅当 $gcd(a,m)|b$ 时方程才有解。

3、代码注意点：

（1）在数学意义上 $a\equiv b(modm)\to b=a-\lfloor \frac{a}{m}\rfloor \cdot m$ 对于负数也是一样的。

13、中国剩余定理

1、目标：用来求一种特殊的线性同余方程组。
$$\{\begin{array}{c}x\equiv a_1\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_1\right)\\ x\equiv a_2\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_2\right)\\ ⋮\\ x\equiv a_n\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_n\right)\end{array}$$
假设 $m_1,m_2,\cdots ,m_n$ 两两互质，那么对于任意整数 $a_1,a_2,\cdots ,a_n$ 上述方程有解。令 $M={\prod }_{i=1}^n{m}_i$ ， M i = M m i , i ∈ { 1 , 2 , ⋯ , n } M_i = \frac{M}{m_i}, i \in \{1,2,\cdots, n \} Mi​=mi​M​,i∈{1,2,⋯,n} ，设 $t_i=M_i^{-1}$ 为 $M_i$ 模 $m_i$ 的逆元。则解为：
$$x=a_1{t}_1{M}_1+a_2{t}_2{M}_2+\cdots +a_n{t}_n{M}_n+kM=kM+\sum _{i=1}^n{a}_i{t}_i{M}_i,k\in \mathbb{Z}$$
如果再模上 $M$ 则方程的解为：$x=\left({\sum }_{i=1}^n{a}_i{t}_i{M}_i\right)\mathrm{m}\mathrm{o}\mathrm{d}M$ ，可以这样求得最小正整数解。

2、应用：最经典的例子就是韩信点兵：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

由题意得：
$$\{\begin{array}{c}x\equiv 2(mod3)\\ x\equiv 3(mod5)\\ x\equiv 2(mod7)\end{array}$$

$a_i$	$2$	$3$	$2$
$M_i$	$3$5	$21$	$15$
$t_i$	$2$	$1$	$1$

则 $x=2\times 35\times 2+3\times 21\times 1+2\times 15\times 1+105k=105k+233,k\in \mathbb{Z}$ 所以最小的正整数解应该是23

3、变形：中国剩余定理只有当 $m_1,m_2,\cdots ,m_n$ 两两互质 时才成立。如果没有这样的限制条件该如何处理？
$$\{\begin{array}{c}x\equiv a_1\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_1\right)\\ x\equiv a_2\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_2\right)\\ ⋮\\ x\equiv a_n\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_n\right)\end{array}$$
首先只研究前两个方程：
$$\{\begin{array}{c}x\equiv a_1(modm1)\\ x\equiv a_2(mod{m}_2)\end{array}$$
可以转化为：
$$\{\begin{array}{c}x=k_1\cdot m_1+a_1\\ x=k_2\cdot m_2+a_2\end{array}$$
整理得：
$$\begin{gathered} k_1\cdot m_1+a_1=k_2\cdot m_2+a_2 \\ {k}_1\cdot m_1-k_2\cdot m_2=a_2-a_1 \end{gathered}$$
上式中，$m_1,m_2,a_1,a_2$ 已知，根据扩展欧几里得法我们知道，要想此方程有解需要满足：$gcd(m_1,m_2)|a_2-a_1$ ，记 $d=gcd(m_1,m_2)$，接下来一步比较关键，采用了一个简单的构造法，令 $k_1=k_1+\lambda \cdot \frac{m_2}{d},k_2=k_2+\lambda \cdot \frac{m_1}{d}$ ，代入原方程得：
$$x\prime =(k_1+\lambda \cdot \frac{m_2}{d})\cdot m_1+a_1=k_1\cdot m_1+a_1+\lambda \cdot \frac{m_1\cdot m_2}{d}=x+\lambda \cdot \frac{m_1\cdot m_2}{d}$$
也就是说我们能够把两个方程合并成一个方程！如果记 $\lambda \cdot \frac{m_1\cdot m_2}{d}=m\prime$那么依次类推最终 $n$ 个方程将会合并成一个方程：$x=x_0+\lambda \cdot m\prime$ ，要求最小非负 $x$ ，根据之前中国剩余定理解的形式，要求最小非负的解只要求：$x_0\mathrm{m}\mathrm{o}\mathrm{d}m\prime$

4、代码注意点：

（1）代码中要求最小正整数解的常用操作是： x = (x % M + M) % M

14、高斯消元解线性方程组

1、目标：求解线性方程组

2、思路：首先找到最大的列主元，将其所在行换到首行，并将改行每个元素除以列主元，然后用当前行把剩下行的列主元所在列都消成0，重复此过程，如果最后有效方程的个数小于未知数的个数则有无穷多组解，如果出现了 $0=n,n\ne 0$ 则无解。否则再从最后一行开始向上迭代求出每个解。

3、代码注意点：

（1）注意esp的类型是 double ！！！

（2）注意gauss( )函数内的 c, r，不要定义在循环体内。

15、组合数

1、题型分类：

2、递归法

1、思路：$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$ 它的含义是，假如从 $a$ 个苹果中选 $b$ 个，我们可以先挑出来一个苹果，然后就有两种情况：一是我们决定要选择这个，那么接下来就在剩下的 $a-1$ 个苹果中再选择 $b-1$ 个，二是我们决定不选这个，那么就在剩下的 $a-1$ 个中选择 $b$ 个。所以我们可以创建一个二维数组来存储每一种组合数的值。

2、代码注意点：

（1）记得初始化一个都不取的情况为 1

3、预处理逆元

1、思路：根据求组合数的公式：$C_a^b=\frac{A_a^b}{b!}=\frac{a!}{b!(a-b)!}$ ，可以预处理出分子分母，这里需要注意，由于最后要求的其实是 $C_a^b\mathrm{m}\mathrm{o}\mathrm{d}m$ 但是

$ (\frac{x}{y}\mod m) \neq \frac{x\mod m}{y\mod m}$ ，所以要求分母对模数的逆元，这样可以把除法转换成乘法并且不影响结果。

2、代码注意点：

（1）注意 fact[0] = infact[0] = 1

4、Lucas 定理

1、公式：若 $p$ 是质数，则对 $\forall 1\le b\le a$ 有 $C_a^b=C_{amodp}^{bmodp}\cdot C_{a/p}^{b/p}\mathrm{m}\mathrm{o}\mathrm{d}p$

2、代码注意点：

（1）根据定义求组合数的模板要记住！

int c(int a, int b, int p){if(b > a) return 0;int res = 1;for(int i = a, j = 1; j <= b; i--, j++){res = (LL)res * i % p;res = (LL)res * qmi(j, p - 2, p) % p;}return res;
}

5、分解质因数 + 高精度

1、思路：当我们需要求出组合数的真实值，而非对某个数的余数时，我们可以转换思路，组合数的真实值可以表达成若干个素数的乘积，所以我们只需要做如下几件事：

• 用线性筛法求出范围内的所有质数
• 通过 $C_a^b=\frac{a!}{b!(a-b)!}$ 这个公式求出每个质因子的次数。 $n!$ 中 $p$ 的次数是 $n/p+n/p^2+n/p^3+\cdots$
• 用高精度乘法将所有质因子相乘

2、代码注意点：

（1）用高精度乘法将所有质因子相乘的时候是两层循环，第一层遍历所有质因子，第二层的作用相当于是求质因子的对应次方的值。

16、明安图-卡特兰数

1、公式：
$$C_n=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$$

17、容斥原理

1、公式：
$$\left|\bigcup _{i=1}^n{A}_i\right|=\sum _{i=1}^n\left|A_i\right|-\sum _{1⩽i<j⩽n}\left|A_i\cap A_j\right|+\sum _{1⩽i<j<k⩽n}\left|A_i\cap A_j\cap A_k\right|-\cdots +(-1{)}^{n-1}\left|A_1\cap \cdots \cap A_n\right|$$

$$\left|\bigcup _{i=1}^n{A}_i\right|=\sum _{k=1}^n(-1{)}^{k+1}\left(\sum _{1⩽i_1<\cdots <i_k⩽n}\left|A_{i_1}\cap \cdots \cap A_{i_k}\right|\right)$$

2、时间复杂度：$O(2^n)$

3、代码注意点：

（1）根据组合恒等式：${\sum }_{i=0}^n{C}_n^i=2^n$ ，$k$ 个集合共有 $2^k-1$ 种选法，排除了一个集合都不选的情况。针对这种类型的枚举，一个常用的技巧是位运算。枚举从 1 到 $2^k-1$ 的每个数的形式，如 果第 $n$ 位是0，就代表不选第 $n$ 个集合，如果是 1 就代表选择这个集合。

比如有三个集合 $S_1,S_2,S_3$ ，显然共有 7 种组合方式：$S_1,S_2,S_3,S_1\cap S_2,S_1\cap S_3,S_2\cap S_3,S_1\cap S_2\cap S_3$ ，1 到 7 的二进制数正好能够不重不漏地包含这些情况。001，010， 011， 100， 101， 110，111

（2）一个 $n$ 为的二进制数能够左移的范围应该是 0 ~ n - 1 位。

（3）$[1,n],n>1,n\in \mathbb{Z}$ 的区间内，能被 $t,t\in [1,n]$ 整除的数的个数是 $\lfloor \frac{n}{t}\rfloor$