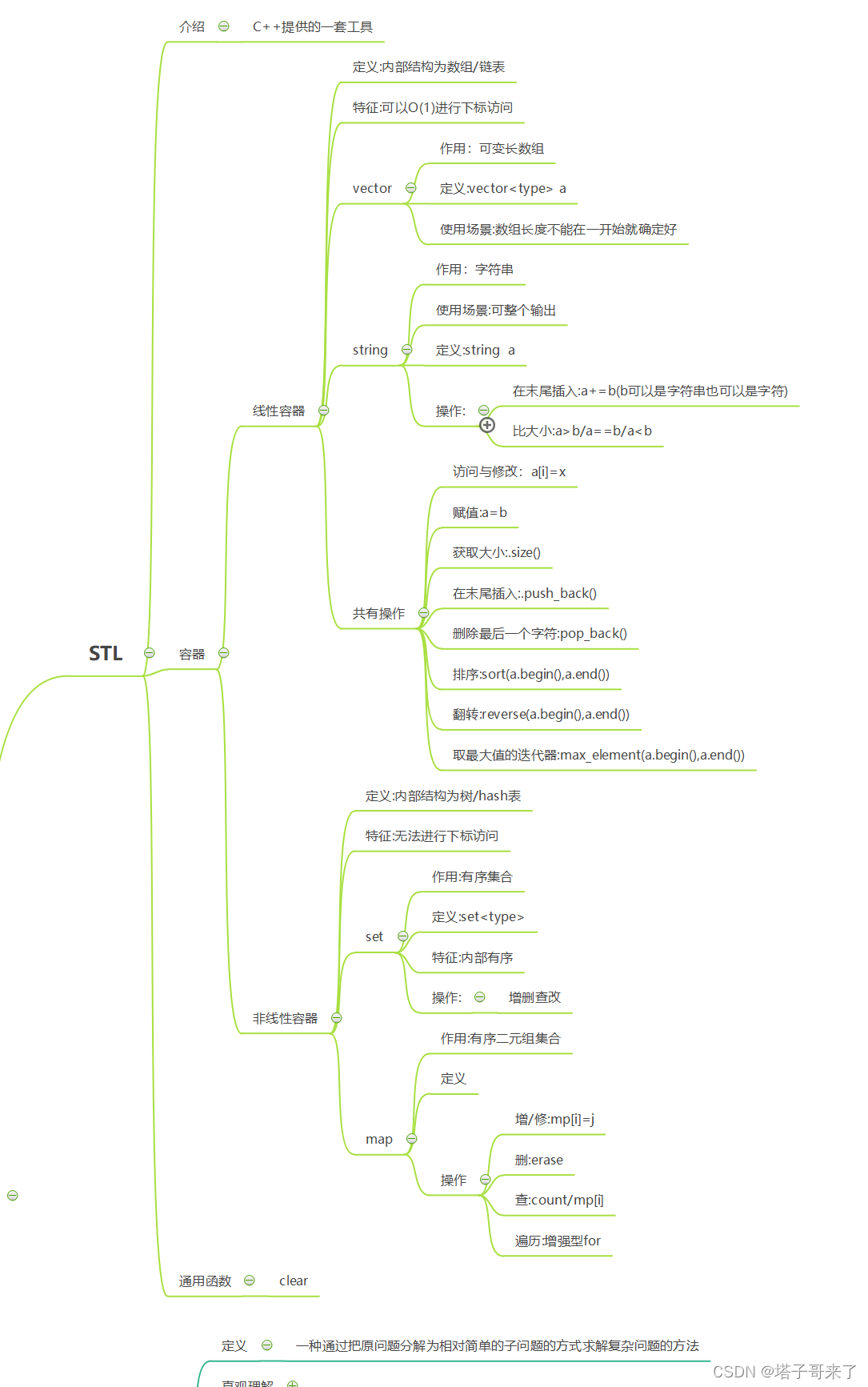
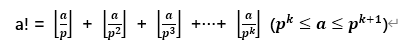文章目录
- 第七节课
- 1、二叉树
- 1.1.二叉树的先序、中序、后序遍历
- 1.2二叉树的按层遍历
- 二叉树的最大宽度:
- 1.3二叉树的序列化和反序列化
- 第八节课
- 1、题目一
- 2、题目二
- 3、折纸
- 4、二叉树的递归套路
- 题目一
- 题目二
- 题目三
- 派对的最大快乐
- 第九节课
- 1、打表法
- 1.1题目一
- 1.2题目二
- 1.3 题目三
- 1.4打表找规律
- 2 . 矩阵处理技巧
- 2.1 Zzigzag 打印矩阵
- 2.2 转圈打印矩阵
- 2.3 原地旋转正方形矩阵
- 第十节课
- 1、贪心算法
- 1.1贪心算法求解的标准过程
- 1.2贪心算法的解题套路
- 题目一
- 题目二
- 题目三
- 题目四
- 2、并查集
- 第十二节课
- Dijkstra算法
- 暴力递归
- 汉诺塔问题
- 逆序栈
- 第十三节课
- 1.字符串子序列
- 2.字符串全排列
- 3.从左往右的尝试模型:
- 4.从左往右的尝试模型---背包问题
- 5.范围上尝试的模型
- 第十四节课
- 1.N皇后
- 2.题目一
- 第十五节课
- 1.背包问题
- 2、十三节课三,五题
- 3、换钱的最少货币数目
- 第十六节课
- 题目二
- 1.1加傻缓存的暴力递归
- 总结:
- 什么暴力递归可以优化
- 暴力递归与动态规划的关系
- 找动态规划的路线
- 原则:
- 暴力递归到动态规划的套路
- 多样本位置全对应的尝试模型
- 2、两个字符串的最长公共子序列问题
- 寻找业务限制的尝试模型
第七节课
1、二叉树
1.1.二叉树的先序、中序、后序遍历
先序:任何子树的处理顺序都是,先头节点、再左子树、然后右子树
中序:任何子树的处理顺序都是,先左子树、再头节点、然后右子树
后序:任何子树的处理顺序都是,先左子树、再右子树、然后头节点
public static class Node {public int value; public Node left;public Node right;public Node(int v) {value = v;}}public static void f(Node head) {if (head == null) {return;}// 1f(head.left);// 2f(head.right);// 3}// 先序打印所有节点public static void pre(Node head) {if (head == null) {return;}System.out.println(head.value);pre(head.left);pre(head.right);}public static void in(Node head) {if (head == null) {return;}in(head.left);System.out.println(head.value);in(head.right);}public static void pos(Node head) {if (head == null) {return;}pos(head.left);pos(head.right);System.out.println(head.value);}
非递归方式实现二叉树的先中后序:
public static class Node {public int value;public Node left;public Node right;public Node(int v) {value = v;}}public static void pre(Node head) {System.out.print("pre-order: ");if (head != null) {Stack<Node> stack = new Stack<Node>();stack.add(head);while (!stack.isEmpty()) {head = stack.pop();System.out.print(head.value + " ");if (head.right != null) {stack.push(head.right);}if (head.left != null) {stack.push(head.left);}}}System.out.println();}public static void in(Node cur) {System.out.print("in-order: ");if (cur != null) {Stack<Node> stack = new Stack<Node>();while (!stack.isEmpty() || cur != null) {if (cur != null) {stack.push(cur);cur = cur.left;} else {cur = stack.pop();System.out.print(cur.value + " ");cur = cur.right;}}}System.out.println();}public static void pos1(Node head) {System.out.print("pos-order: ");if (head != null) {Stack<Node> s1 = new Stack<Node>();Stack<Node> s2 = new Stack<Node>();s1.push(head);while (!s1.isEmpty()) {head = s1.pop(); // 头 右 左s2.push(head);if (head.left != null) {s1.push(head.left);}if (head.right != null) {s1.push(head.right);}}// 左 右 头while (!s2.isEmpty()) {System.out.print(s2.pop().value + " ");}}System.out.println();}//炫技版本public static void pos2(Node h) {System.out.print("pos-order: ");if (h != null) {Stack<Node> stack = new Stack<Node>();stack.push(h);Node c = null;while (!stack.isEmpty()) {c = stack.peek();if (c.left != null && h != c.left && h != c.right) {stack.push(c.left);} else if (c.right != null && h != c.right) {stack.push(c.right);} else {System.out.print(stack.pop().value + " ");h = c;}}}System.out.println();}
1.2二叉树的按层遍历
- 宽度优先遍历,用队列
- 设置flag变量的方式,来发现某一层的结束
public static void level(Node head) {if (head == null) {return;}Queue<Node> queue = new LinkedList<>();queue.add(head);while (!queue.isEmpty()) {Node cur = queue.poll();System.out.println(cur.value);if (cur.left != null) {queue.add(cur.left);}if (cur.right != null) {queue.add(cur.right);}}}
二叉树的最大宽度:
public static int maxWidthUseMap(Node head) {if (head == null) {return 0;}Queue<Node> queue = new LinkedList<>();queue.add(head);// key 在 哪一层,valueHashMap<Node, Integer> levelMap = new HashMap<>();levelMap.put(head, 1);int curLevel = 1; // 当前你正在统计哪一层的宽度int curLevelNodes = 0; // 当前层curLevel层,宽度目前是多少int max = 0;while (!queue.isEmpty()) {Node cur = queue.poll();int curNodeLevel = levelMap.get(cur);if (cur.left != null) {levelMap.put(cur.left, curNodeLevel + 1);queue.add(cur.left);}if (cur.right != null) {levelMap.put(cur.right, curNodeLevel + 1);queue.add(cur.right);}if (curNodeLevel == curLevel) {curLevelNodes++;} else {max = Math.max(max, curLevelNodes);curLevel++;curLevelNodes = 1;}}max = Math.max(max, curLevelNodes);return max;}public static int maxWidthNoMap(Node head) {if (head == null) {return 0;}Queue<Node> queue = new LinkedList<>();queue.add(head);Node curEnd = head; // 当前层,最右节点是谁Node nextEnd = null; // 下一层,最右节点是谁int max = 0;int curLevelNodes = 0; // 当前层的节点数while (!queue.isEmpty()) {Node cur = queue.poll();if (cur.left != null) {queue.add(cur.left);nextEnd = cur.left;}if (cur.right != null) {queue.add(cur.right);nextEnd = cur.right;}curLevelNodes++;if (cur == curEnd) {max = Math.max(max, curLevelNodes);curLevelNodes = 0;curEnd = nextEnd;}}return max;}
1.3二叉树的序列化和反序列化
1)可以用先序或者中序或者后序或者按层遍历,来实现二叉树的序列化
2)用了什么方式序列化,就用什么样的方式反序列化
public static Queue<String> preSerial(Node head) {Queue<String> ans = new LinkedList<>();pres(head, ans);return ans;}public static void pres(Node head, Queue<String> ans) {if (head == null) {ans.add(null);} else {ans.add(String.valueOf(head.value));pres(head.left, ans);pres(head.right, ans);}}public static Queue<String> inSerial(Node head) {Queue<String> ans = new LinkedList<>();ins(head, ans);return ans;}public static void ins(Node head, Queue<String> ans) {if (head == null) {ans.add(null);} else {ins(head.left, ans);ans.add(String.valueOf(head.value));ins(head.right, ans);}}public static Queue<String> posSerial(Node head) {Queue<String> ans = new LinkedList<>();poss(head, ans);return ans;}public static void poss(Node head, Queue<String> ans) {if (head == null) {ans.add(null);} else {poss(head.left, ans);poss(head.right, ans);ans.add(String.valueOf(head.value));}}public static Node buildByPreQueue(Queue<String> prelist) {if (prelist == null || prelist.size() == 0) {return null;}return preb(prelist);}public static Node preb(Queue<String> prelist) {String value = prelist.poll();if (value == null) {return null;}Node head = new Node(Integer.valueOf(value));head.left = preb(prelist);head.right = preb(prelist);return head;}public static Node buildByPosQueue(Queue<String> poslist) {if (poslist == null || poslist.size() == 0) {return null;}// 左右中 -> stack(中右左)Stack<String> stack = new Stack<>();while (!poslist.isEmpty()) {stack.push(poslist.poll());}return posb(stack);}public static Node posb(Stack<String> posstack) {String value = posstack.pop();if (value == null) {return null;}Node head = new Node(Integer.valueOf(value));head.right = posb(posstack);head.left = posb(posstack);return head;}public static Queue<String> levelSerial(Node head) {Queue<String> ans = new LinkedList<>();if (head == null) {ans.add(null);} else {ans.add(String.valueOf(head.value));Queue<Node> queue = new LinkedList<Node>();queue.add(head);while (!queue.isEmpty()) {head = queue.poll(); // head 父 子if (head.left != null) {ans.add(String.valueOf(head.left.value));queue.add(head.left);} else {ans.add(null);}if (head.right != null) {ans.add(String.valueOf(head.right.value));queue.add(head.right);} else {ans.add(null);}}}return ans;}public static Node buildByLevelQueue(Queue<String> levelList) {if (levelList == null || levelList.size() == 0) {return null;}Node head = generateNode(levelList.poll());Queue<Node> queue = new LinkedList<Node>();if (head != null) {queue.add(head);}Node node = null;while (!queue.isEmpty()) {node = queue.poll();node.left = generateNode(levelList.poll());node.right = generateNode(levelList.poll());if (node.left != null) {queue.add(node.left);}if (node.right != null) {queue.add(node.right);}}return head;}public static Node generateNode(String val) {if (val == null) {return null;}return new Node(Integer.valueOf(val));}第八节课
1、题目一
如何设计一个打印整棵树的打印函数
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static void printTree(Node head) {System.out.println("Binary Tree:");printInOrder(head, 0, "H", 17);System.out.println();}public static void printInOrder(Node head, int height, String to, int len) {if (head == null) {return;}printInOrder(head.right, height + 1, "v", len);String val = to + head.value + to;int lenM = val.length();int lenL = (len - lenM) / 2;int lenR = len - lenM - lenL;val = getSpace(lenL) + val + getSpace(lenR);System.out.println(getSpace(height * len) + val);printInOrder(head.left, height + 1, "^", len);}public static String getSpace(int num) {String space = " ";StringBuffer buf = new StringBuffer("");for (int i = 0; i < num; i++) {buf.append(space);}return buf.toString();}public static void main(String[] args) {Node head = new Node(1);head.left = new Node(-222222222);head.right = new Node(3);head.left.left = new Node(Integer.MIN_VALUE);head.right.left = new Node(55555555);head.right.right = new Node(66);head.left.left.right = new Node(777);printTree(head);head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.right.left = new Node(5);head.right.right = new Node(6);head.left.left.right = new Node(7);printTree(head);head = new Node(1);head.left = new Node(1);head.right = new Node(1);head.left.left = new Node(1);head.right.left = new Node(1);head.right.right = new Node(1);head.left.left.right = new Node(1);printTree(head);}
2、题目二
Class Node {V value;Node left;Node right;Node parents;
}
//给你一个二叉树中的某个节点,返回该节点的后继节点
public static class Node {public int value;public Node left;public Node right;public Node parent;public Node(int data) {this.value = data;}}public static Node getSuccessorNode(Node node) {if (node == null) {return node;}if (node.right != null) {return getLeftMost(node.right);} else { // 无右子树Node parent = node.parent;while (parent != null && parent.right == node) { // 当前节点是其父亲节点右孩子node = parent;parent = node.parent;}return parent;}}public static Node getLeftMost(Node node) {if (node == null) {return node;}while (node.left != null) {node = node.left;}return node;}public static void main(String[] args) {Node head = new Node(6);head.parent = null;head.left = new Node(3);head.left.parent = head;head.left.left = new Node(1);head.left.left.parent = head.left;head.left.left.right = new Node(2);head.left.left.right.parent = head.left.left;head.left.right = new Node(4);head.left.right.parent = head.left;head.left.right.right = new Node(5);head.left.right.right.parent = head.left.right;head.right = new Node(9);head.right.parent = head;head.right.left = new Node(8);head.right.left.parent = head.right;head.right.left.left = new Node(7);head.right.left.left.parent = head.right.left;head.right.right = new Node(10);head.right.right.parent = head.right;Node test = head.left.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.left.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.right.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.left.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.right; // 10's next is nullSystem.out.println(test.value + " next: " + getSuccessorNode(test));}
3、折纸
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数 N ,代表纸条都从下边向上方连续对折 N 次。请从上到下打印所有折痕的方向。
例如: N =1时,打印: downN =2时,打印: down down up
public static void printAllFolds(int N) {process(1, N, true);System.out.println();}// 当前你来了一个节点,脑海中想象的!// 这个节点在第i层,一共有N层,N固定不变的// 这个节点如果是凹的话,down = T// 这个节点如果是凸的话,down = F// 函数的功能:中序打印以你想象的节点为头的整棵树!public static void process(int i, int N, boolean down) {if (i > N) {return;}process(i + 1, N, true);System.out.print(down ? "凹 " : "凸 ");process(i + 1, N, false);}
4、二叉树的递归套路
1)假设以 x 节点为头,设可以向 X 左树和 X 右树要任何信息
2)在上一步的假设下,讨论以 X 为头节点的树,得到答案的可能性(最重要)
3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息
4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S
5)递归函数都返回 S ,每一棵子树都这么要求
6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
题目一
给定一颗二叉树的头结点head,返回这颗二叉树是不是平衡二叉树
平衡二叉树:每一个子树的左树与右树的高度差不超过1;
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static boolean isBalanced1(Node head) {boolean[] ans = new boolean[1];ans[0] = true;process1(head, ans);return ans[0];}public static int process1(Node head, boolean[] ans) {if (!ans[0] || head == null) {return -1;}int leftHeight = process1(head.left, ans);int rightHeight = process1(head.right, ans);if (Math.abs(leftHeight - rightHeight) > 1) {ans[0] = false;}return Math.max(leftHeight, rightHeight) + 1;}public static boolean isBalanced2(Node head) {return process(head).isBalanced;}public static class Info{public boolean isBalanced;public int height;public Info(boolean i, int h) {isBalanced = i;height = h;}}public static Info process(Node x) {if(x == null) {return new Info(true, 0);}Info leftInfo = process(x.left);Info rightInfo = process(x.right);int height = Math.max(leftInfo.height, rightInfo.height) + 1;boolean isBalanced = true;if(!leftInfo.isBalanced) {isBalanced = false;}if(!rightInfo.isBalanced) {isBalanced = false;}if(Math.abs(leftInfo.height - rightInfo.height) > 1) {isBalanced = false;}return new Info(isBalanced, height);}
题目二
给定一颗二叉树的头结点head,任何两个节点之间都存在距离,返回整颗二叉树的最大距离
//暴力与递归
public static class Node {public int value;public Node left;public Node right;public Node(int data) {this.value = data;}}public static int maxDistance1(Node head) {if (head == null) {return 0;}ArrayList<Node> arr = getPrelist(head);HashMap<Node, Node> parentMap = getParentMap(head);int max = 0;for (int i = 0; i < arr.size(); i++) {for (int j = i; j < arr.size(); j++) {max = Math.max(max, distance(parentMap, arr.get(i), arr.get(j)));}}return max;}public static ArrayList<Node> getPrelist(Node head) {ArrayList<Node> arr = new ArrayList<>();fillPrelist(head, arr);return arr;}public static void fillPrelist(Node head, ArrayList<Node> arr) {if (head == null) {return;}arr.add(head);fillPrelist(head.left, arr);fillPrelist(head.right, arr);}public static HashMap<Node, Node> getParentMap(Node head) {HashMap<Node, Node> map = new HashMap<>();map.put(head, null);fillParentMap(head, map);return map;}public static void fillParentMap(Node head, HashMap<Node, Node> parentMap) {if (head.left != null) {parentMap.put(head.left, head);fillParentMap(head.left, parentMap);}if (head.right != null) {parentMap.put(head.right, head);fillParentMap(head.right, parentMap);}}public static int distance(HashMap<Node, Node> parentMap, Node o1, Node o2) {HashSet<Node> o1Set = new HashSet<>();Node cur = o1;o1Set.add(cur);while (parentMap.get(cur) != null) {cur = parentMap.get(cur);o1Set.add(cur);}cur = o2;while (!o1Set.contains(cur)) {cur = parentMap.get(cur);}Node lowestAncestor = cur;cur = o1;int distance1 = 1;while (cur != lowestAncestor) {cur = parentMap.get(cur);distance1++;}cur = o2;int distance2 = 1;while (cur != lowestAncestor) {cur = parentMap.get(cur);distance2++;}return distance1 + distance2 - 1;}public static int maxDistance2(Node head) {return process(head).maxDistance;}public static class Info {public int maxDistance;public int height;public Info(int m, int h) {maxDistance = m;height = h;}}public static Info process(Node x) {if (x == null) {return new Info(0, 0);}Info leftInfo = process(x.left);Info rightInfo = process(x.right);int height = Math.max(leftInfo.height, rightInfo.height) + 1;int p1 = leftInfo.maxDistance;int p2 = rightInfo.maxDistance;int p3 = leftInfo.height + rightInfo.height + 1;int maxDistance = Math.max(Math.max(p1, p2), p3);return new Info(maxDistance, height);}题目三
给定一颗二叉树的头结点head,返回这颗二叉树最大的二叉搜索子树的头结点
搜索二叉树:左树的值小于节点,右树的值大于节点
// 在线测试链接 : https://leetcode.com/problems/largest-bst-subtree
// 提交时不要提交这个类public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int value) {val = value;}}// 提交如下的largestBSTSubtree方法,可以直接通过public static int largestBSTSubtree(TreeNode head) {if (head == null) {return 0;}return process(head).maxBSTSubtreeSize;}public static class Info {public int maxBSTSubtreeSize;public int allSize;public int max;public int min;public Info(int m, int a, int ma, int mi) {maxBSTSubtreeSize = m;allSize = a;max = ma;min = mi;}}public static Info process(TreeNode x) {if (x == null) {return null;}Info leftInfo = process(x.left);Info rightInfo = process(x.right);int max = x.val;int min = x.val;int allSize = 1;if (leftInfo != null) {max = Math.max(leftInfo.max, max);min = Math.min(leftInfo.min, min);allSize += leftInfo.allSize;}if (rightInfo != null) {max = Math.max(rightInfo.max, max);min = Math.min(rightInfo.min, min);allSize += rightInfo.allSize;}int p1 = -1;if (leftInfo != null) {p1 = leftInfo.maxBSTSubtreeSize;}int p2 = -1;if (rightInfo != null) {p2 = rightInfo.maxBSTSubtreeSize;}int p3 = -1;boolean leftBST = leftInfo == null ? true : (leftInfo.maxBSTSubtreeSize == leftInfo.allSize);boolean rightBST = right Info == null ? true : (rightInfo.maxBSTSubtreeSize == rightInfo.allSize);if (leftBST && rightBST) {boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < x.val);boolean rightMinMoreX = rightInfo == null ? true : (x.val < rightInfo.min);if (leftMaxLessX && rightMinMoreX) {int leftSize = leftInfo == null ? 0 : leftInfo.allSize;int rightSize = rightInfo == null ? 0 : rightInfo.allSize;p3 = leftSize + rightSize + 1;}}return new Info(Math.max(p1, Math.max(p2, p3)), allSize, max, min);}
派对的最大快乐
员工信息定义如下:
class Employee{
public int happy; //这名员工可以带来的欢乐值
List subordinates; //这名员工有哪些直接下级
}
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、没有环的多又树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。叶节点是没有任何下属的基层员工( subordinates 列表为空),除基层员工外,每个员工都有一个或多个直接下级。
这个公司现在要办 party ,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点 boss ,请返回派对的最大快乐值。
public static class Employee {public int happy;public List<Employee> nexts;public Employee(int h) {happy = h;nexts = new ArrayList<>();}}public static int maxHappy1(Employee boss) {if (boss == null) {return 0;}return process1(boss, false);}// 当前来到的节点叫cur,// up表示cur的上级是否来,// 该函数含义:// 如果up为true,表示在cur上级已经确定来,的情况下,cur整棵树能够提供最大的快乐值是多少?// 如果up为false,表示在cur上级已经确定不来,的情况下,cur整棵树能够提供最大的快乐值是多少?public static int process1(Employee cur, boolean up) {if (up) { // 如果cur的上级来的话,cur没得选,只能不来int ans = 0;for (Employee next : cur.nexts) {ans += process1(next, false);}return ans;} else { // 如果cur的上级不来的话,cur可以选,可以来也可以不来int p1 = cur.happy;int p2 = 0;for (Employee next : cur.nexts) {p1 += process1(next, true);p2 += process1(next, false);}return Math.max(p1, p2);}}public static int maxHappy2(Employee head) {Info allInfo = process(head);return Math.max(allInfo.no, allInfo.yes);}public static class Info {public int no;public int yes;public Info(int n, int y) {no = n;yes = y;}}public static Info process(Employee x) {if (x == null) {return new Info(0, 0);}int no = 0;int yes = x.happy;for (Employee next : x.nexts) {Info nextInfo = process(next);no += Math.max(nextInfo.no, nextInfo.yes);yes += nextInfo.no;}return new Info(no, yes);}
第九节课
1、打表法
1)问题如果返回值不太多,可以用 hardcode 的方式列出,作为程序的一部分
2)个大问题解决时底层频繁使用规模不大的小问题的解,如果小问题的返回值满足条件1),可以把小问题的解列成一张表,作为程序的一部分
3)打表找规律(本节课重点)
1.1题目一
小虎去买苹果,商店只提供两种类型的塑料袋,每种类型都有任意数量。
1)能装下6个苹果的袋子
2)能装下8个苹果的袋子
小虎可以自由使用两种袋子来装苹果,但是小虎有强迫症,他要求自己使用的袋子数量必须最少,且使用的每个袋子必须装满。给定一个正整数 N ,返回至少使用多少袋子。如果 N 无法让使用的每个袋子必须装满,返回﹣1
public static int minBags(int apple) {if (apple < 0) {return -1;}int bag8 = (apple >> 3);int rest = apple - (bag8 << 3);while(bag8 >= 0) {// rest 个if(rest % 6 ==0) {return bag8 + (rest / 6);} else {bag8--;rest += 8;}}return -1;}public static int minBagAwesome(int apple) {if ((apple & 1) != 0) { // 如果是奇数,返回-1return -1;}if (apple < 18) {return apple == 0 ? 0 : (apple == 6 || apple == 8) ? 1: (apple == 12 || apple == 14 || apple == 16) ? 2 : -1;}return (apple - 18) / 8 + 3;}public static void main(String[] args) {for(int apple = 1; apple < 200;apple++) {System.out.println(apple + " : "+ minBags(apple));}}
打表找规律
1)某个面试题,输入参数类型简单,并且只有一个实际参数
2)要求的返回值类型也简单,并且只有一个
3)用暴力方法,把输入参数对应的返回值,打印出来看看,进而优化 code
1.2题目二
给定一个正整数 N ,表示有 N 份青草统一堆放在仓库里有一只牛和一只羊,牛先吃,羊后吃,它俩轮流吃草不管是牛还是羊,每一轮能吃的草量必须是:1,4,16,64·(4的某次方)
谁最先把草吃完,谁获胜
假设牛和羊都绝顶聪明,都想赢,都会做出理性的决定根据唯一的参数 N ,返回谁会赢
public static String whoWin(int n) {if (n < 5) {return n == 0 || n == 2 ? "后手" : "先手";}// 进到这个过程里来,当前的先手,先选int want = 1;while (want <= n) {if (whoWin(n - want).equals("后手")) {return "先手";}if (want <= (n / 4)) {want *= 4;} else {break;}}return "后手";}public static String winner1(int n) {if (n < 5) {return (n == 0 || n == 2) ? "后手" : "先手";}int base = 1;while (base <= n) {if (winner1(n - base).equals("后手")) {return "先手";}if (base > n / 4) { // 防止base*4之后溢出break;}base *= 4;}return "后手";}public static String winner2(int n) {if (n % 5 == 0 || n % 5 == 2) {return "后手";} else {return "先手";}}
1.3 题目三
定义一种数:可以表示成若干(数量>1)连续正数和的数
比如:
5=2+3, 5就是这样的数
12=3+4+5, 12就是这样的数
1不是这样的数,因为要求数量大于1个、连续正数和
2=1+1,2也不是,因为等号右边不是连续正数
给定一个参数 N ,返回是不是可以表示成若干连续正数和的数
public static boolean isMSum1(int num) {for (int start = 1; start <= num; start++) {int sum = start;for (int j = start + 1; j <= num; j++) {if (sum + j > num) {break;}if (sum + j == num) {return true;}sum += j;}}return false;}public static boolean isMSum2(int num) {
//
// return num == (num & (~num + 1));
//
// return num == (num & (-num));//num不是2的某次方 反之 是return (num & (num - 1)) != 0;}public static void main(String[] args) {for (int num = 1; num < 200; num++) {System.out.println(num + " : " + isMSum1(num));}System.out.println("test begin");for (int num = 1; num < 5000; num++) {if (isMSum1(num) != isMSum2(num)) {System.out.println("Oops!");}}System.out.println("test end");}
1.4打表找规律
1)某个面试题,输入参数类型简单,并且只有一个实际参数
2)要求的返回值类型也简单,并且只有一个
3)用暴力方法,把输入参数对应的返回值,打印出来看看,进而优化
2 . 矩阵处理技巧
核心技巧:找到 coding 上的宏观调度
2.1 Zzigzag 打印矩阵
public static void printMatrixZigZag(int[][] matrix) {int tR = 0;int tC = 0;int dR = 0;int dC = 0;int endR = matrix.length - 1;int endC = matrix[0].length - 1;boolean fromUp = false;while (tR != endR + 1) {printLevel(matrix, tR, tC, dR, dC, fromUp);tR = tC == endC ? tR + 1 : tR;tC = tC == endC ? tC : tC + 1;dC = dR == endR ? dC + 1 : dC;dR = dR == endR ? dR : dR + 1;fromUp = !fromUp;}System.out.println();}public static void printLevel(int[][] m, int tR, int tC, int dR, int dC, boolean f) {if (f) {while (tR != dR + 1) {System.out.print(m[tR++][tC--] + " ");}} else {while (dR != tR - 1) {System.out.print(m[dR--][dC++] + " ");}}}public static void main(String[] args) {int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };printMatrixZigZag(matrix);}
2.2 转圈打印矩阵
public static void spiralOrderPrint(int[][] matrix) {int tR = 0;int tC = 0;int dR = matrix.length - 1;int dC = matrix[0].length - 1;while (tR <= dR && tC <= dC) {printEdge(matrix, tR++, tC++, dR--, dC--);}}public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {if (tR == dR) {for (int i = tC; i <= dC; i++) {System.out.print(m[tR][i] + " ");}} else if (tC == dC) {for (int i = tR; i <= dR; i++) {System.out.print(m[i][tC] + " ");}} else {int curC = tC;int curR = tR;while (curC != dC) {System.out.print(m[tR][curC] + " ");curC++;}while (curR != dR) {System.out.print(m[curR][dC] + " ");curR++;}while (curC != tC) {System.out.print(m[dR][curC] + " ");curC--;}while (curR != tR) {System.out.print(m[curR][tC] + " ");curR--;}}}public static void main(String[] args) {int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },{ 13, 14, 15, 16 } };spiralOrderPrint(matrix);}
2.3 原地旋转正方形矩阵
public static void rotate(int[][] matrix) {int a = 0;int b = 0;int c = matrix.length - 1;int d = matrix[0].length - 1;while (a < c) {rotateEdge(matrix, a++, b++, c--, d--);}}public static void rotateEdge(int[][] m, int a, int b, int c, int d) {int tmp = 0;for (int i = 0; i < d - b; i++) {tmp = m[a][b + i];m[a][b + i] = m[c - i][b];m[c - i][b] = m[c][d - i];m[c][d - i] = m[a + i][d];m[a + i][d] = tmp;}}public static void printMatrix(int[][] matrix) {for (int i = 0; i != matrix.length; i++) {for (int j = 0; j != matrix[0].length; j++) {System.out.print(matrix[i][j] + " ");}System.out.println();}}public static void main(String[] args) {int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 }, { 13, 14, 15, 16 } };printMatrix(matrix);rotate(matrix);System.out.println("=========");printMatrix(matrix);}
第十节课
1、贪心算法
1)最自然智慧的算法
2)用一种局部最功利的标准,总是做出在当前看来是最好的选择
3)难点在于证明局部最功利的标准可以得到全局最优解
4)对于贪心算法的学习主要以增加阅历和经验为主
从头到尾讲一道利用贪心算法求解的题目:
给定一个由字符串组成的数组 strs ,必须把所有的字符串拼接起来,返回所有可能的拼接结果中,字典序最小的结果
1.1贪心算法求解的标准过程
1,分析业务
2,根据业务逻辑找到不同的贪心策略
3,对于能举出反例的策略直接跳过,不能举出反例的策略要证明有效性这往往是特别困难的,要求数学能力很高且不具有统一的技巧性
1.2贪心算法的解题套路
1,实现一个不依靠贪心策略的解法 X ,可以用最暴力的尝试
2,脑补出贪心策略 A 、贪心策略 B 、贪心策略 C …
3,用解法 X 和对数器,用实验的方式得知哪个贪心策略正确
4,不要去纠结贪心策略的证明
题目一
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。
给你每一个项目开始的时间和结束的时间你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。
返回最多的宣讲场次
public static class Program {public int start;public int end;public Program(int start, int end) {this.start = start;this.end = end;}}// 暴力!所有情况都尝试!public static int bestArrange1(Program[] programs) {if (programs == null || programs.length == 0) {return 0;}return process(programs, 0, 0);}// 还剩下的会议都放在programs里// done之前已经安排了多少会议的数量// timeLine目前来到的时间点是什么// 目前来到timeLine的时间点,已经安排了done多的会议,剩下的会议programs可以自由安排// 返回能安排的最多会议数量public static int process(Program[] programs, int done, int timeLine) {if (programs.length == 0) {return done;}// 还剩下会议int max = done;// 当前安排的会议是什么会,每一个都枚举for (int i = 0; i < programs.length; i++) {if (programs[i].start >= timeLine) {Program[] next = copyButExcept(programs, i);max = Math.max(max, process(next, done + 1, programs[i].end));}}return max;}public static Program[] copyButExcept(Program[] programs, int i) {Program[] ans = new Program[programs.length - 1];int index = 0;for (int k = 0; k < programs.length; k++) {if (k != i) {ans[index++] = programs[k];}}return ans;}// 会议的开始时间和结束时间,都是数值,不会 < 0public static int bestArrange2(Program[] programs) {Arrays.sort(programs, new ProgramComparator());int timeLine = 0;int result = 0;// 依次遍历每一个会议,结束时间早的会议先遍历for (int i = 0; i < programs.length; i++) {if (timeLine <= programs[i].start) {result++;timeLine = programs[i].end;}}return result;}public static class ProgramComparator implements Comparator<Program> {@Overridepublic int compare(Program o1, Program o2) {return o1.end - o2.end;}}
题目二
给定一个字符串 str ,只由’ X 和’.'两种字符构成。
’ X 表示墙,不能放灯,也不需要点亮
'.'表示居民点,可以放灯,需要点亮
如果灯放在 i 位置,可以让 i -1,和 i +1三个位置被点亮
返回如果点亮 str 中所有需要点亮的位置,至少需要几盏灯
public static int minLight1(String road) {if (road == null || road.length() == 0) {return 0;}return process(road.toCharArray(), 0, new HashSet<>());}// str[index....]位置,自由选择放灯还是不放灯// str[0..index-1]位置呢?已经做完决定了,那些放了灯的位置,存在lights里// 要求选出能照亮所有.的方案,并且在这些有效的方案中,返回最少需要几个灯public static int process(char[] str, int index, HashSet<Integer> lights) {if (index == str.length) { // 结束的时候for (int i = 0; i < str.length; i++) {if (str[i] != 'X') { // 当前位置是点的话if (!lights.contains(i - 1) && !lights.contains(i) && !lights.contains(i + 1)) {return Integer.MAX_VALUE;}}}return lights.size();} else { // str还没结束// i X .int no = process(str, index + 1, lights);int yes = Integer.MAX_VALUE;if (str[index] == '.') {lights.add(index);yes = process(str, index + 1, lights);lights.remove(index);}return Math.min(no, yes);}}public static int minLight2(String road) {char[] str = road.toCharArray();int i = 0;int light = 0;while (i < str.length) {if (str[i] == 'X') {i++;} else {light++;if (i + 1 == str.length) {break;} else { // 有i位置 i+ 1 X .if (str[i + 1] == 'X') {i = i + 2;} else {i = i + 3;}}}}return light;}// 更简洁的解法// 两个X之间,数一下.的数量,然后除以3,向上取整// 把灯数累加public static int minLight3(String road) {char[] str = road.toCharArray();int cur = 0;int light = 0;for (char c : str) {if (c == 'X') {light += (cur + 2) / 3;cur = 0;} else {cur++;}}light += (cur + 2) / 3;return light;}
题目三
一块金条切成两半,是需要花费和长度数值一样的铜板的。
比如长度为20的金条,不管怎么切,都要花费20个铜板。一群人想整分整块金条,怎么分最省铜板?
例如给定数组(10,20,30},代表一共三个人,整块金条长度为60,金条要分成10,20,30三个部分。
如果先把长度60的金条分成10和50,花费60;再把长度50的金条分成20和30,花费50;一共花费110铜板。但如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20,花费30;一共花费90铜板。
输入一个数组,返回分割的最小代价。
// 纯暴力!public static int lessMoney1(int[] arr) {if (arr == null || arr.length == 0) {return 0;}return process(arr, 0);}// 等待合并的数都在arr里,pre之前的合并行为产生了多少总代价// arr中只剩一个数字的时候,停止合并,返回最小的总代价public static int process(int[] arr, int pre) {if (arr.length == 1) {return pre;}int ans = Integer.MAX_VALUE;for (int i = 0; i < arr.length; i++) {for (int j = i + 1; j < arr.length; j++) {ans = Math.min(ans, process(copyAndMergeTwo(arr, i, j), pre + arr[i] + arr[j]));}}return ans;}public static int[] copyAndMergeTwo(int[] arr, int i, int j) {int[] ans = new int[arr.length - 1];int ansi = 0;for (int arri = 0; arri < arr.length; arri++) {if (arri != i && arri != j) {ans[ansi++] = arr[arri];}}ans[ansi] = arr[i] + arr[j];return ans;}public static int lessMoney2(int[] arr) {PriorityQueue<Integer> pQ = new PriorityQueue<>();for (int i = 0; i < arr.length; i++) {pQ.add(arr[i]);}int sum = 0;int cur = 0;while (pQ.size() > 1) {cur = pQ.poll() + pQ.poll();sum += cur;pQ.add(cur);}return sum;}
题目四
输入:正数数组 costs 、正数数组 profits 、正数 K 、正数 M
costs [i]表示i号项目的花费
profits [i]表示i号项目在扣除花费之后还能挣到的钱(利润)
K 表示你只能串行的最多做 k 个项目
M 表示你初始的资金说明:每做完一个项目,马上获得的收益,可以支持你去做下一个项目。
不能并行的做项目。输出:你最后获得的最大钱数。
// 最多K个项目// W是初始资金// Profits[] Capital[] 一定等长// 返回最终最大的资金public static int findMaximizedCapital(int K, int W, int[] Profits, int[] Capital) {PriorityQueue<Program> minCostQ = new PriorityQueue<>(new MinCostComparator());PriorityQueue<Program> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());for (int i = 0; i < Profits.length; i++) {minCostQ.add(new Program(Profits[i], Capital[i]));}for (int i = 0; i < K; i++) {while (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {maxProfitQ.add(minCostQ.poll());}if (maxProfitQ.isEmpty()) {return W;}W += maxProfitQ.poll().p;}return W;}public static class Program {public int p;public int c;public Program(int p, int c) {this.p = p;this.c = c;}}public static class MinCostComparator implements Comparator<Program> {@Overridepublic int compare(Program o1, Program o2) {return o1.c - o2.c;}}public static class MaxProfitComparator implements Comparator<Program> {@Overridepublic int compare(Program o1, Program o2) {return o2.p - o1.p;}}
2、并查集
1)有若干个样本 a 、 b 、 C 、 d ..类型假设是V
2)在并查集中一开始认为每个样本都在单独的集合里
3)用户可以在任何时候调用如下两个方法:
boolean isSameSet ( Vx , Vy ):查询样本×和样本 y 是否属于一个集合
void union ( Vx , Vy ):把 x 和 y 各自所在集合的所有样本合并成一个集合
- isSameSet 和 union 方法的代价越低越好
public static class Node<V> {V value;public Node(V v) {value = v;}}public static class UnionFind<V> {public HashMap<V, Node<V>> nodes;public HashMap<Node<V>, Node<V>> parents;public HashMap<Node<V>, Integer> sizeMap;public UnionFind(List<V> values) {nodes = new HashMap<>();parents = new HashMap<>();sizeMap = new HashMap<>();for (V cur : values) {Node<V> node = new Node<>(cur);nodes.put(cur, node);parents.put(node, node);sizeMap.put(node, 1);}}// 给你一个节点,请你往上到不能再往上,把代表返回public Node<V> findFather(Node<V> cur) {Stack<Node<V>> path = new Stack<>();while (cur != parents.get(cur)) {path.push(cur);cur = parents.get(cur);}while (!path.isEmpty()) {parents.put(path.pop(), cur);}return cur;}public boolean isSameSet(V a, V b) {return findFather(nodes.get(a)) == findFather(nodes.get(b));}public void union(V a, V b) {Node<V> aHead = findFather(nodes.get(a));Node<V> bHead = findFather(nodes.get(b));if (aHead != bHead) {int aSetSize = sizeMap.get(aHead);int bSetSize = sizeMap.get(bHead);Node<V> big = aSetSize >= bSetSize ? aHead : bHead;Node<V> small = big == aHead ? bHead : aHead;parents.put(small, big);sizeMap.put(big, aSetSize + bSetSize);sizeMap.remove(small);}}public int sets() {return sizeMap.size();}}
第十二节课
Dijkstra算法
public static HashMap<Node, Integer> dijkstra1(Node from) {HashMap<Node, Integer> distanceMap = new HashMap<>();distanceMap.put(from, 0);// 打过对号的点HashSet<Node> selectedNodes = new HashSet<>();Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);while (minNode != null) {// 原始点 -> minNode(跳转点) 最小距离distanceint distance = distanceMap.get(minNode);for (Edge edge : minNode.edges) {Node toNode = edge.to;if (!distanceMap.containsKey(toNode)) {distanceMap.put(toNode, distance + edge.weight);} else { // toNode distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));}}selectedNodes.add(minNode);minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);}return distanceMap;}public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> touchedNodes) {Node minNode = null;int minDistance = Integer.MAX_VALUE;for (Entry<Node, Integer> entry : distanceMap.entrySet()) {Node node = entry.getKey();int distance = entry.getValue();if (!touchedNodes.contains(node) && distance < minDistance) {minNode = node;minDistance = distance;}}return minNode;}public static class NodeRecord {public Node node;public int distance;public NodeRecord(Node node, int distance) {this.node = node;this.distance = distance;}}public static class NodeHeap {private Node[] nodes; // 实际的堆结构// key 某一个node, value 上面堆中的位置private HashMap<Node, Integer> heapIndexMap;// key 某一个节点, value 从源节点出发到该节点的目前最小距离private HashMap<Node, Integer> distanceMap;private int size; // 堆上有多少个点public NodeHeap(int size) {nodes = new Node[size];heapIndexMap = new HashMap<>();distanceMap = new HashMap<>();size = 0;}public boolean isEmpty() {return size == 0;}// 有一个点叫node,现在发现了一个从源节点出发到达node的距离为distance// 判断要不要更新,如果需要的话,就更新public void addOrUpdateOrIgnore(Node node, int distance) {if (inHeap(node)) {distanceMap.put(node, Math.min(distanceMap.get(node), distance));insertHeapify(heapIndexMap.get(node));}if (!isEntered(node)) {nodes[size] = node;heapIndexMap.put(node, size);distanceMap.put(node, distance);insertHeapify(size++);}}public NodeRecord pop() {NodeRecord nodeRecord = new NodeRecord(nodes[0], distanceMap.get(nodes[0]));swap(0, size - 1);heapIndexMap.put(nodes[size - 1], -1);distanceMap.remove(nodes[size - 1]);// free C++同学还要把原本堆顶节点析构,对java同学不必nodes[size - 1] = null;heapify(0, --size);return nodeRecord;}private void insertHeapify(int index) {while (distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])) {swap(index, (index - 1) / 2);index = (index - 1) / 2;}}private void heapify(int index, int size) {int left = index * 2 + 1;while (left < size) {int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distanceMap.get(nodes[left])? left + 1: left;smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]) ? smallest : index;if (smallest == index) {break;}swap(smallest, index);index = smallest;left = index * 2 + 1;}}private boolean isEntered(Node node) {return heapIndexMap.containsKey(node);}private boolean inHeap(Node node) {return isEntered(node) && heapIndexMap.get(node) != -1;}private void swap(int index1, int index2) {heapIndexMap.put(nodes[index1], index2);heapIndexMap.put(nodes[index2], index1);Node tmp = nodes[index1];nodes[index1] = nodes[index2];nodes[index2] = tmp;}}// 改进后的dijkstra算法// 从head出发,所有head能到达的节点,生成到达每个节点的最小路径记录并返回public static HashMap<Node, Integer> dijkstra2(Node head, int size) {NodeHeap nodeHeap = new NodeHeap(size);nodeHeap.addOrUpdateOrIgnore(head, 0);HashMap<Node, Integer> result = new HashMap<>();while (!nodeHeap.isEmpty()) {NodeRecord record = nodeHeap.pop();Node cur = record.node;int distance = record.distance;for (Edge edge : cur.edges) {nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);}result.put(cur, distance);}return result;}
暴力递归
- 思想:
- 把问题转化为规模缩小的同类问题的子问题
- 有明确的的不需要继续进行递归的条件
- 有当得到了子问题的结果之后的决策的过程
- 不记录每一个子问题的解
汉诺塔问题
public static void hanoi1(int n) {leftToRight(n);}// 请把1~N层圆盘 从左 -> 右public static void leftToRight(int n) {if (n == 1) { // base caseSystem.out.println("Move 1 from left to right");return;}leftToMid(n - 1);System.out.println("Move " + n + " from left to right");midToRight(n - 1);}// 请把1~N层圆盘 从左 -> 中public static void leftToMid(int n) {if (n == 1) {System.out.println("Move 1 from left to mid");return;}leftToRight(n - 1);System.out.println("Move " + n + " from left to mid");rightToMid(n - 1);}public static void rightToMid(int n) {if (n == 1) {System.out.println("Move 1 from right to mid");return;}rightToLeft(n - 1);System.out.println("Move " + n + " from right to mid");leftToMid(n - 1);}public static void midToRight(int n) {if (n == 1) {System.out.println("Move 1 from mid to right");return;}midToLeft(n - 1);System.out.println("Move " + n + " from mid to right");leftToRight(n - 1);}public static void midToLeft(int n) {if (n == 1) {System.out.println("Move 1 from mid to left");return;}midToRight(n - 1);System.out.println("Move " + n + " from mid to left");rightToLeft(n - 1);}public static void rightToLeft(int n) {if (n == 1) {System.out.println("Move 1 from right to left");return;}rightToMid(n - 1);System.out.println("Move " + n + " from right to left");midToLeft(n - 1);}public static void hanoi2(int n) {if (n > 0) {func(n, "left", "right", "mid");}}public static void func(int N, String from, String to, String other) {if (N == 1) { // baseSystem.out.println("Move 1 from " + from + " to " + to);} else {func(N - 1, from, other, to);System.out.println("Move " + N + " from " + from + " to " + to);func(N - 1, other, to, from);}}public static void hanoi3(int N) {if (N < 1) {return;}Stack<Record> stack = new Stack<>();stack.add(new Record(false, N, "left", "right", "mid"));while (!stack.isEmpty()) {Record cur = stack.pop();if (cur.base == 1) {System.out.println("Move 1 from " + cur.from + " to " + cur.to);if (!stack.isEmpty()) {stack.peek().finish1 = true;}} else {if (!cur.finish1) {stack.push(cur);stack.push(new Record(false, cur.base - 1, cur.from, cur.other, cur.to));} else {System.out.println("Move " + cur.base + " from " + cur.from + " to " + cur.to);stack.push(new Record(false, cur.base - 1, cur.other, cur.to, cur.from));}}}}
逆序栈
要求:不申请额外的数据结构 使用递归
public static void reserve(Stack<Integer> stack)
{if(stack.isEmpty()){return ;}int i = f(stack);reserve(stack);stack.push(i);
}public static int f(Stack<Integer> stack)
{int result = stack.pop();if(stack.isEmpty()){return result;}else {int last = f(stack)stack.push(result);return last;}}
第十三节课
1.字符串子序列
- 打印一个字符的全部子序列
- 打印一个字符的全部子序列,要求不要出现重复字面的值的子序列
打印一个字符的全部子序列// s -> "abc" ->public static List<String> subs(String s) {char[] str = s.toCharArray();String path = "";List<String> ans = new ArrayList<>();process1(str, 0, ans, path);return ans;}// str 固定参数// 来到了str[index]字符,index是位置// str[0..index-1]已经走过了!之前的决定,都在path上// 之前的决定已经不能改变了,就是path// str[index....]还能决定,之前已经确定,而后面还能自由选择的话,// 把所有生成的子序列,放入到ans里去public static void process1(char[] str, int index, List<String> ans, String path) {if (index == str.length) {ans.add(path);return;}// 没有要index位置的字符process1(str, index + 1, ans, path);// 要了index位置的字符process1(str, index + 1, ans, path + String.valueOf(str[index]));}public static List<String> subsNoRepeat(String s) {char[] str = s.toCharArray();String path = "";HashSet<String> set = new HashSet<>();process2(str, 0, set, path);List<String> ans = new ArrayList<>();for (String cur : set) {ans.add(cur);}return ans;}打印一个字符的全部子序列,要求不要出现重复字面的值的子序列public static void process2(char[] str, int index, HashSet<String> set, String path) {if (index == str.length) {set.add(path);return;}String no = path;process2(str, index + 1, set, no);String yes = path + String.valueOf(str[index]);process2(str, index + 1, set, yes);}
2.字符串全排列
- 打印一个字符串的全部排列
- 打印一个字符串的全部排列,要求不要出现重复的排列
public static List<String> permutation1(String s) {List<String> ans = new ArrayList<>();if (s == null || s.length() == 0) {return ans;}char[] str = s.toCharArray(); ArrayList<Character> rest = new ArrayList<Character>();for (char cha : str) {rest.add(cha);}String path = "";f(rest, path, ans);return ans;}public static void f(ArrayList<Character> rest, String path, List<String> ans) {if (rest.isEmpty()) {ans.add(path);} else {int N = rest.size();for (int i = 0; i < N; i++) {char cur = rest.get(i);rest.remove(i);f(rest, path + cur, ans);rest.add(i, cur);}}}//打印一个字符串的全部排列public static List<String> permutation2(String s) {List<String> ans = new ArrayList<>();if (s == null || s.length() == 0) {return ans;}char[] str = s.toCharArray();g1(str, 0, ans);return ans;}public static void g1(char[] str, int index, List<String> ans) {if (index == str.length) {ans.add(String.valueOf(str));} else {for (int i = index; i < str.length; i++) {swap(str, index, i);g1(str, index + 1, ans);swap(str, index, i);}}}public static List<String> permutation3(String s) {List<String> ans = new ArrayList<>();if (s == null || s.length() == 0) {return ans;}char[] str = s.toCharArray();g2(str, 0, ans);return ans;}public static void g2(char[] str, int index, List<String> ans) {if (index == str.length) {ans.add(String.valueOf(str));} else {boolean[] visited = new boolean[256];for (int i = index; i < str.length; i++) {if (!visited[str[i]]) {visited[str[i]] = true;swap(str, index, i);g2(str, index + 1, ans);swap(str, index, i);}}}}public static void swap(char[] chs, int i, int j) {char tmp = chs[i];chs[i] = chs[j];chs[j] = tmp;}public static void main(String[] args) {String s = "acc";List<String> ans1 = permutation1(s);for (String str : ans1) {System.out.println(str);}System.out.println("=======");List<String> ans2 = permutation2(s);for (String str : ans2) {System.out.println(str);}System.out.println("=======");List<String> ans3 = permutation3(s);for (String str : ans3) {System.out.println(str);}}
3.从左往右的尝试模型:
规定1和 A 对应、2和 B 对应、3和 C 对应..
那么一个数字字符串比如"111"就可以转化为:" AAA “、” KA "和" AK "
给定一个只有数字字符组成的字符串 str ,返回有多少种转化结果
// str只含有数字字符0~9// 返回多少种转化方案public static int number(String str) {if (str == null || str.length() == 0) {return 0;}return process(str.toCharArray(), 0);}// str[0..i-1]转化无需过问// str[i.....]去转化,返回有多少种转化方法public static int process(char[] str, int i) {if (i == str.length) {return 1;}// i没到最后,说明有字符if (str[i] == '0') { // 之前的决定有问题return 0;}// str[i] != '0'// 可能性一,i单转int ways = process(str, i + 1);if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) {ways += process(str, i + 2);}return ways;}// 从右往左的动态规划// 就是上面方法的动态规划版本// dp[i]表示:str[i...]有多少种转化方式public static int dp1(String s) {if (s == null || s.length() == 0) {return 0;}char[] str = s.toCharArray();int N = str.length;int[] dp = new int[N + 1];dp[N] = 1;for (int i = N - 1; i >= 0; i--) {if (str[i] != '0') {int ways = dp[i + 1];if (i + 1 < str.length && (str[i] - '0') * 10 + str[i + 1] - '0' < 27) {ways += dp[i + 2];}dp[i] = ways;}}return dp[0];}// 从左往右的动态规划// dp[i]表示:str[0...i]有多少种转化方式public static int dp2(String s) {if (s == null || s.length() == 0) {return 0;}char[] str = s.toCharArray();int N = str.length;if (str[0] == '0') {return 0;}int[] dp = new int[N];dp[0] = 1;for (int i = 1; i < N; i++) {if (str[i] == '0') {// 如果此时str[i]=='0',那么他是一定要拉前一个字符(i-1的字符)一起拼的,// 那么就要求前一个字符,不能也是‘0’,否则拼不了。// 前一个字符不是‘0’就够了嘛?不够,还得要求拼完了要么是10,要么是20,如果更大的话,拼不了。// 这就够了嘛?还不够,你们拼完了,还得要求str[0...i-2]真的可以被分解!// 如果str[0...i-2]都不存在分解方案,那i和i-1拼成了也不行,因为之前的搞定不了。if (str[i - 1] == '0' || str[i - 1] > '2' || (i - 2 >= 0 && dp[i - 2] == 0)) {return 0;} else {dp[i] = i - 2 >= 0 ? dp[i - 2] : 1;}} else {dp[i] = dp[i - 1];if (str[i - 1] != '0' && (str[i - 1] - '0') * 10 + str[i] - '0' <= 26) {dp[i] += i - 2 >= 0 ? dp[i - 2] : 1;}}}return dp[N - 1];}
4.从左往右的尝试模型—背包问题
给定两个长度都为 N 的数组 weights和 values , weights,
weights[i]和 values [i]分别代表号物品的重量和价值。
给定一个正数 bag ,表示一个载重 bag 的袋子,你装的物品不能超过这个重量。
返回你能装下最多的价值是多少?
// 所有的货,重量和价值,都在w和v数组里// 为了方便,其中没有负数// bag背包容量,不能超过这个载重// 返回:不超重的情况下,能够得到的最大价值public static int maxValue(int[] w, int[] v, int bag) {if (w == null || v == null || w.length != v.length || w.length == 0) {return 0;}// 尝试函数!return process(w, v, 0, bag);}// index 0~N// rest 负~bagpublic static int process(int[] w, int[] v, int index, int rest) {if (rest < 0) {return -1;}if (index == w.length) {return 0;}int p1 = process(w, v, index + 1, rest);int p2 = 0;int next = process(w, v, index + 1, rest - w[index]);if (next != -1) {p2 = v[index] + next;}return Math.max(p1, p2);}public static int dp(int[] w, int[] v, int bag) {if (w == null || v == null || w.length != v.length || w.length == 0) {return 0;}int N = w.length;int[][] dp = new int[N + 1][bag + 1];for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= bag; rest++) {int p1 = dp[index + 1][rest];int p2 = 0;int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];if (next != -1) {p2 = v[index] + next;}dp[index][rest] = Math.max(p1, p2);}}return dp[0][bag];}
5.范围上尝试的模型
给定一个整型数组 arr ,代表数值不同的纸牌排成一条线,
玩家 A 和玩家 B 依次拿走每张纸牌,
规定玩家 A 先拿,玩家 B 后拿,
但是每个玩家每次只能拿走最左或最右的纸牌,
玩家 A 和玩家 B 都绝顶聪明。请返回最后获胜者的分数。
// 根据规则,返回获胜者的分数public static int win1(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int first = f1(arr, 0, arr.length - 1);int second = g1(arr, 0, arr.length - 1);return Math.max(first, second);}// arr[L..R],先手获得的最好分数返回public static int f1(int[] arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g1(arr, L + 1, R);int p2 = arr[R] + g1(arr, L, R - 1);return Math.max(p1, p2);}// // arr[L..R],后手获得的最好分数返回public static int g1(int[] arr, int L, int R) {if (L == R) {return 0;}int p1 = f1(arr, L + 1, R); // 对手拿走了L位置的数int p2 = f1(arr, L, R - 1); // 对手拿走了R位置的数return Math.min(p1, p2);}public static int win2(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {fmap[i][j] = -1;gmap[i][j] = -1;}}int first = f2(arr, 0, arr.length - 1, fmap, gmap);int second = g2(arr, 0, arr.length - 1, fmap, gmap);return Math.max(first, second);}// arr[L..R],先手获得的最好分数返回public static int f2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R) {ans = arr[L];} else {int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);ans = Math.max(p1, p2);}fmap[L][R] = ans;return ans;}// // arr[L..R],后手获得的最好分数返回public static int g2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (gmap[L][R] != -1) {return gmap[L][R];}int ans = 0;if (L != R) {int p1 = f2(arr, L + 1, R, fmap, gmap); // 对手拿走了L位置的数int p2 = f2(arr, L, R - 1, fmap, gmap); // 对手拿走了R位置的数ans = Math.min(p1, p2);}gmap[L][R] = ans;return ans;}public static int win3(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}return Math.max(fmap[0][N - 1], gmap[0][N - 1]);}
第十四节课
1.N皇后
N 皇后问题是指在 N * N 的棋盘上要摆 N 个皇后,
要求任何两个皇后不同行、不同列,也不在同一条斜线上
给定一个整数 n ,返回 n 皇后的摆法有多少种。
n =1,返回1 n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0n=8,返回92
public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}// 当前来到i行,一共是0~N-1行// 在i行上放皇后,所有列都尝试// 必须要保证跟之前所有的皇后不打架// int[] record record[x] = y 之前的第x行的皇后,放在了y列上// 返回:不关心i以上发生了什么,i.... 后续有多少合法的方法数public static int process1(int i, int[] record, int n) {if (i == n) {return 1;}int res = 0;// i行的皇后,放哪一列呢?j列,for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}return res;}public static boolean isValid(int[] record, int i, int j) {// 0..i-1for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}// 请不要超过32皇后问题public static int num2(int n) {if (n < 1 || n > 32) {return 0;}// 如果你是13皇后问题,limit 最右13个1,其他都是0int limit = n == 32 ? -1 : (1 << n) - 1;return process2(limit, 0, 0, 0);}// 7皇后问题// limit : 0....0 1 1 1 1 1 1 1// 之前皇后的列影响:colLim// 之前皇后的左下对角线影响:leftDiaLim// 之前皇后的右下对角线影响:rightDiaLimpublic static int process2(int limit, int colLim, int leftDiaLim, int rightDiaLim) {if (colLim == limit) {return 1;}// pos中所有是1的位置,是你可以去尝试皇后的位置int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));int mostRightOne = 0;int res = 0;while (pos != 0) {mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(limit, colLim | mostRightOne, (leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);}return res;}
2.题目一
假设有排成一行的 N 个位置,记为1~ N , N 一定大于或等于2
开始时机器人在其中的 M 位置上( M 一定是1~ N 中的一个)
如果机器人来到1位置,那么下一步只能往右来到2位置;
如果机器人来到 N 位置,那么下一步只能往左来到 N -1位置;
如果机器人来到中间位置,那么下一步可以往左走或者往右走;
规定机器人必须走 K 步,最终能来到 P 位置( P 也是1~ N 中的一个)的方法有多少种
给定四个参数 N 、 M 、 K 、 P ,返回方法数。
public static int ways1(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}return process1(start, K, aim, N);}// 机器人当前来到的位置是cur,// 机器人还有rest步需要去走,// 最终的目标是aim,// 有哪些位置?1~N// 返回:机器人从cur出发,走过rest步之后,最终停在aim的方法数,是多少?public static int process1(int cur, int rest, int aim, int N) {if (rest == 0) { // 如果已经不需要走了,走完了!return cur == aim ? 1 : 0;}// (cur, rest)if (cur == 1) { // 1 -> 2return process1(2, rest - 1, aim, N);}// (cur, rest)if (cur == N) { // N-1 <- Nreturn process1(N - 1, rest - 1, aim, N);}// (cur, rest)return process1(cur - 1, rest - 1, aim, N) + process1(cur + 1, rest - 1, aim, N);}public static int ways2(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}int[][] dp = new int[N + 1][K + 1];for (int i = 0; i <= N; i++) {for (int j = 0; j <= K; j++) {dp[i][j] = -1;}}// dp就是缓存表// dp[cur][rest] == -1 -> process1(cur, rest)之前没算过!// dp[cur][rest] != -1 -> process1(cur, rest)之前算过!返回值,dp[cur][rest]// N+1 * K+1return process2(start, K, aim, N, dp);}// cur 范: 1 ~ N// rest 范:0 ~ Kpublic static int process2(int cur, int rest, int aim, int N, int[][] dp) {if (dp[cur][rest] != -1) {return dp[cur][rest];}// 之前没算过!int ans = 0;if (rest == 0) {ans = cur == aim ? 1 : 0;} else if (cur == 1) {ans = process2(2, rest - 1, aim, N, dp);} else if (cur == N) {ans = process2(N - 1, rest - 1, aim, N, dp);} else {ans = process2(cur - 1, rest - 1, aim, N, dp) + process2(cur + 1, rest - 1, aim, N, dp);}dp[cur][rest] = ans;return ans;}public static int ways3(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}int[][] dp = new int[N + 1][K + 1];dp[aim][0] = 1;for (int rest = 1; rest <= K; rest++) {dp[1][rest] = dp[2][rest - 1];for (int cur = 2; cur < N; cur++) {dp[cur][rest] = dp[cur - 1][rest - 1] + dp[cur + 1][rest - 1];}dp[N][rest] = dp[N - 1][rest - 1];}return dp[start][K];}
第十五节课
1.背包问题
// 所有的货,重量和价值,都在w和v数组里// 为了方便,其中没有负数// bag背包容量,不能超过这个载重// 返回:不超重的情况下,能够得到的最大价值public static int maxValue(int[] w, int[] v, int bag) {if (w == null || v == null || w.length != v.length || w.length == 0) {return 0;}// 尝试函数!return process(w, v, 0, bag);}// index 0~N// rest 负~bagpublic static int process(int[] w, int[] v, int index, int rest) {if (rest < 0) {return -1;}if (index == w.length) {return 0;}int p1 = process(w, v, index + 1, rest);int p2 = 0;int next = process(w, v, index + 1, rest - w[index]);if (next != -1) {p2 = v[index] + next;}return Math.max(p1, p2);}public static int dp(int[] w, int[] v, int bag) {if (w == null || v == null || w.length != v.length || w.length == 0) {return 0;}int N = w.length;int[][] dp = new int[N + 1][bag + 1];for (int index = N - 1; index >= 0; index--) {for (int rest = 0; rest <= bag; rest++) {int p1 = dp[index + 1][rest];int p2 = 0;int next = rest - w[index] < 0 ? -1 : dp[index + 1][rest - w[index]];if (next != -1) {p2 = v[index] + next;}dp[index][rest] = Math.max(p1, p2);}}return dp[0][bag];}
2、十三节课三,五题
3、换钱的最少货币数目
【题目】
给定数组 arr,arr 中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数 aim,代表要找的钱数,求组成aim的最少货币数。
【举例】
arr=[5,2,3],aim=20。
4 张 5 元可以组成 20 元,其他的找钱方案都要使用更多张的货币,所以返回4。
arr=[5,2,3],aim=0。
不用任何货币就可以组成 0 元,返回 0。
arr=[3,5],aim=2。
根本无法组成 2 元,钱不能找开的情况下默认返回-1。
3.1暴力
public static int way(int [] arr,int aim)
{if(arr = null || arr.length == 0 || aim < 0){return 0;}return process(arr,0,aim);
}
public static int process(int [] arr,int index,int rest)
{if(index == arr.length){return rest == 0 ? 1 : 0;}int ways = 0;for(int zhang = 0;zhang * arr[index] <= rest;zhang++){ways += process(arr,index +1,rest - (zhang * arr[index]))}return ways;
}
3.2计划搜索
public static int way(int [] arr,int aim)
{if(arr = null || arr.length == 0 || aim < 0){return 0;}int [][] dp = new int [arr.length +1][aim + 1];for(int i = 0;i < dp.length ;i++){for(int j = 0;j < dp[0].length;j++){dp[i][j] == -1;}}return process(arr,0,aim,dp);
}
public static int process(int [] arr,int index,int rest,int [][] dp)
{if(dp[index][rest] != -1){return dp[index][rest];}if(index == arr.length){dp[index][rest] = rest == 0 ? 1 : 0;return dp[index][rest];}int ways = 0;for(int zhang = 0;zhang * arr[index] <= rest;zhang++){ways += process(arr,index +1,rest - (zhang * arr[index]))}dp[index][rest] = ways;return ways;
}
3.3dp
//有枚举行为
public static int way(int [] arr,int aim)
{if(arr = null || arr.length == 0 || aim < 0){return 0;}int N = arr.length;int [][] dp = new int [N +1][aim + 1];dp[N][0] = 1;for(int index = N- 1;index >= 0;index--){for(int rest = 0;rest <= aim;rest++){int ways = 0;for(int zhang = 0;zhang * arr[index] <= rest;zhang++){ways += dp[index +1][rest - (zhang * arr[index])];}dp[index][rest] = ways;}}return dp[0][aim];
}
//无枚举行为
public static int way(int [] arr,int aim)
{if(arr = null || arr.length == 0 || aim < 0){return 0;}int N = arr.length;int [][] dp = new int [N +1][aim + 1];dp[N][0] = 1;for(int index = N- 1;index >= 0;index--){for(int rest = 0;rest <= aim;rest++){dp[index][rest] = dp[index + 1][rest];if(rest - arr[index] >= 0){ dp[index][rest] += dp[index][rest - arr[index])];}}}return dp[0][aim];
}
第十六节课
题目二
给定一个字符串 str ,给定一个字符串类型的数组 arr 。
arr 里的每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出 str 来。
返回需要至少多少张贴纸可以完成这个任务。
例子: str =" babac “, arr ={” ba “,“℃”,” abcd “}至少需要两张贴纸” ba "和’ abcd ",因为使用这两张贴纸,把每一个字符单独剪开,含有2个 a 、2个 b 、1个 C 。是可以拼出 str 的。所以返回2。
1.1加傻缓存的暴力递归
public static int minStickers3(String[] stickers, String target) {int N = stickers.length;int[][] counts = new int[N][26];//统计每个贴纸的字母的数目for (int i = 0; i < N; i++) {char[] str = stickers[i].toCharArray();for (char cha : str) {counts[i][cha - 'a']++;}}HashMap<String, Integer> dp = new HashMap<>();dp.put("", 0);int ans = process3(counts, target, dp);return ans == Integer.MAX_VALUE ? -1 : ans;}public static int process3(int[][] stickers, String t, HashMap<String, Integer> dp) {if (dp.containsKey(t)) {return dp.get(t);}char[] target = t.toCharArray();int[] tcounts = new int[26];for (char cha : target) {tcounts[cha - 'a']++;}int N = stickers.length; //贴纸的种类int min = Integer.MAX_VALUE; //使用最少贴纸for (int i = 0; i < N; i++) {//从当前第一张贴纸开始枚举int[] sticker = stickers[i];/*if(sticker[i][target[0] - 'a'] == 0){continue;}可以替换 if (sticker[i][target[0] - 'a'] > 0) {*/if (sticker[i][target[0] - 'a'] > 0) {StringBuilder builder = new StringBuilder();for (int j = 0; j < 26; j++) { if (tcounts[j] > 0) {//还需要当前字符int nums = tcounts[j] - sticker[j];for (int k = 0; k < nums; k++) {builder.append((char) (j + 'a'));}}}//以上就是这个贴纸用完后剩余的字符 字符存放在builder String rest = builder.toString();min = Math.min(min, process3(stickers, rest, dp));}}//如果ans一直是最大值 那么 返回0int ans = min + (min == Integer.MAX_VALUE ? 0 : 1);dp.put(t, ans);return ans;}
// 本题测试链接:https://leetcode.com/problems/stickers-to-spell-word
public static int minStickers1(String[] stickers, String target) {int ans = process1(stickers, target);return ans == Integer.MAX_VALUE ? -1 : ans;}// 所有贴纸stickers,每一种贴纸都有无穷张// target// 最少张数public static int process1(String[] stickers, String target) {if (target.length() == 0) {return 0;}int min = Integer.MAX_VALUE;for (String first : stickers) {String rest = minus(target, first);if (rest.length() != target.length()) {min = Math.min(min, process1(stickers, rest));}}return min + (min == Integer.MAX_VALUE ? 0 : 1);}public static String minus(String s1, String s2) {char[] str1 = s1.toCharArray();char[] str2 = s2.toCharArray();int[] count = new int[26];for (char cha : str1) {count[cha - 'a']++;}for (char cha : str2) {count[cha - 'a']--;}StringBuilder builder = new StringBuilder();for (int i = 0; i < 26; i++) {if (count[i] > 0) {for (int j = 0; j < count[i]; j++) {builder.append((char) (i + 'a'));}}}return builder.toString();}public static int minStickers2(String[] stickers, String target) {int N = stickers.length;// 关键优化(用词频表替代贴纸数组)int[][] counts = new int[N][26];for (int i = 0; i < N; i++) {char[] str = stickers[i].toCharArray();for (char cha : str) {counts[i][cha - 'a']++;}}int ans = process2(counts, target);return ans == Integer.MAX_VALUE ? -1 : ans;}// stickers[i] 数组,当初i号贴纸的字符统计 int[][] stickers -> 所有的贴纸// 每一种贴纸都有无穷张// 返回搞定target的最少张数// 最少张数public static int process2(int[][] stickers, String t) {if (t.length() == 0) {return 0;}// target做出词频统计// target aabbc 2 2 1..// 0 1 2..char[] target = t.toCharArray();int[] tcounts = new int[26];for (char cha : target) {tcounts[cha - 'a']++;}int N = stickers.length;int min = Integer.MAX_VALUE;for (int i = 0; i < N; i++) {// 尝试第一张贴纸是谁int[] sticker = stickers[i];// 最关键的优化(重要的剪枝!这一步也是贪心!)if (sticker[target[0] - 'a'] > 0) {StringBuilder builder = new StringBuilder();for (int j = 0; j < 26; j++) {if (tcounts[j] > 0) {int nums = tcounts[j] - sticker[j];for (int k = 0; k < nums; k++) {builder.append((char) (j + 'a'));}}}String rest = builder.toString();min = Math.min(min, process2(stickers, rest));}}return min + (min == Integer.MAX_VALUE ? 0 : 1);}总结:
什么暴力递归可以优化
- 有重复调用同一个子问题的解 —>可以优化
- 如果每一个子问题都是不同的解—>无法优化也不用优化
暴力递归与动态规划的关系
- 某一个暴力递归,有解的重复调用,就可以把这个暴力递归优化为动态规划
- 任何动态规划问题,都一定对应的这某一个有解的重复调用的暴力递归,反之不一定
找动态规划的路线
- 设置:或者尝试暴力递归做题
- 分析:有无重复的解,
- 优化:有重复操作,记忆搜索,进而以严格的表结构的依赖关系去拿到动态规划
原则:
- 每一个可变参数类型,一定不要比int类型更加复杂
- 原则1违反,让类型突破到一位线性结构,那必须是唯一可变参数
- 原则1违反,2不违反,只需要做到记忆化搜索
- 可变参数尽量少
暴力递归到动态规划的套路
- 你已经有了一个不违反原则的暴力递归,而且的确存在解的重复调用
- 找到哪些参数的变化会影响返回值,对每一个列出变化范围
- 参数间的所有的组合数量,意味着表大小
- 记忆化搜索的方法就是傻缓存,非常容易得到
- 规定好严格表的大小,分析位置的依赖顺序,然后从基础填写到最终解
- 对于有枚举行为的决策过程,进一步优化
多样本位置全对应的尝试模型
2、两个字符串的最长公共子序列问题
public static int longestCommonSubsequence(char[] str1, char[] str2) {int N = str1.length;int M = str2.length;int[][] dp = new int[N][M];dp[0][0] = str1[0] == str2[0] ? 1 : 0;for (int i = 1; i < N; i++) {dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];}for (int j = 1; j < M; j++) {dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];}for (int i = 1; i < N; i++) {for (int j = 1; j < M; j++) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);if (str1[i] == str2[j]) {dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);}}}return dp[N - 1][M - 1];}
// 测试链接:https://leetcode.com/problems/longest-palindromic-subsequence/
未讲解的代码
public static int lpsl1(String s) {if (s == null || s.length() == 0) {return 0;}char[] str = s.toCharArray();return f(str, 0, str.length - 1);}// str[L..R]最长回文子序列长度返回public static int f(char[] str, int L, int R) {if (L == R) {return 1;}if (L == R - 1) {return str[L] == str[R] ? 2 : 1;}int p1 = f(str, L + 1, R - 1);int p2 = f(str, L, R - 1);int p3 = f(str, L + 1, R);int p4 = str[L] != str[R] ? 0 : (2 + f(str, L + 1, R - 1));return Math.max(Math.max(p1, p2), Math.max(p3, p4));}public static int lpsl2(String s) {if (s == null || s.length() == 0) {return 0;}char[] str = s.toCharArray();int N = str.length;int[][] dp = new int[N][N];dp[N - 1][N - 1] = 1;for (int i = 0; i < N - 1; i++) {dp[i][i] = 1;dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;}for (int L = N - 3; L >= 0; L--) {for (int R = L + 2; R < N; R++) {dp[L][R] = Math.max(dp[L][R - 1], dp[L + 1][R]);if (str[L] == str[R]) {dp[L][R] = Math.max(dp[L][R], 2 + dp[L + 1][R - 1]);}}}return dp[0][N - 1];}public static int longestPalindromeSubseq1(String s) {if (s == null || s.length() == 0) {return 0;}if (s.length() == 1) {return 1;}char[] str = s.toCharArray();char[] reverse = reverse(str);return longestCommonSubsequence(str, reverse);}public static char[] reverse(char[] str) {int N = str.length;char[] reverse = new char[str.length];for (int i = 0; i < str.length; i++) {reverse[--N] = str[i];}return reverse;}public static int longestPalindromeSubseq2(String s) {if (s == null || s.length() == 0) {return 0;}if (s.length() == 1) {return 1;}char[] str = s.toCharArray();int N = str.length;int[][] dp = new int[N][N];dp[N - 1][N - 1] = 1;for (int i = 0; i < N - 1; i++) {dp[i][i] = 1;dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;}for (int i = N - 3; i >= 0; i--) {for (int j = i + 2; j < N; j++) {dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);if (str[i] == str[j]) {dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);}}}return dp[0][N - 1];}
寻找业务限制的尝试模型
给定一个数组,代表每个人喝完咖啡准备刷杯子的时间
只有一台咖啡机,一次只能洗一个杯子,时间耗费 a ,洗完才能洗下一杯
每个咖啡杯也可以自己挥发干净,时间耗费 b ,咖啡杯可以并行挥发
返回让所有咖啡杯变干净的最早完成时间
三个参数: int[] ] arr(有序) 、 inta 、intb1
// drinks 所有杯子可以开始洗的时间// wash 单杯洗干净的时间(串行)// air 挥发干净的时间(并行)// free 洗的机器什么时候可用// drinks[index.....]都变干净,最早的结束时间(返回)public static int bestTime(int[] drinks, int wash, int air, int index, int free) {if (index == drinks.length) {return 0;}// index号杯子 决定洗int selfClean1 = Math.max(drinks[index], free) + wash;int restClean1 = bestTime(drinks, wash, air, index + 1, selfClean1);int p1 = Math.max(selfClean1, restClean1);// index号杯子 决定挥发int selfClean2 = drinks[index] + air;int restClean2 = bestTime(drinks, wash, air, index + 1, free);int p2 = Math.max(selfClean2, restClean2);return Math.min(p1, p2);}动态规划:
public static int bestTime(int[] drinks, int wash, int air ) {if(wash <= air){return drinks[drinks.length - 1] + b;}int N = drink.length;int limit = 0;for(int i = 0;i < N;i++){limit = Math.max(limit,drink[i]) + a;}int[][] dp = new int[N][limit + 1];//N-1行所有的值for(int washline = 0;washline <= limit;washline++){dp[N - 1][washline] = Math.min(Math.max(washline,drinks[N - 1]) + wash,drinks[N - 1] + air);}for(int N - 2;index >= 0;index--){for(int washline = 0;washline <= limit;washline++){int p1 = Integer.MAX_VALUE;int wash_1 = Math.max(washline,drinks[index]) + wash;if(wash_1 <= limit){p1 = Math.max(wash,dp[index + 1][wash]);}int p2 = Math.max(drinks[index] + air,dp[index + 1][washline]);dp[index][washline] = Math.min(p1,p2);}}return dp[0][0];
}// 题目
// 数组arr代表每一个咖啡机冲一杯咖啡的时间,每个咖啡机只能串行的制造咖啡。
// 现在有n个人需要喝咖啡,只能用咖啡机来制造咖啡。
// 认为每个人喝咖啡的时间非常短,冲好的时间即是喝完的时间。
// 每个人喝完之后咖啡杯可以选择洗或者自然挥发干净,只有一台洗咖啡杯的机器,只能串行的洗咖啡杯。
// 洗杯子的机器洗完一个杯子时间为a,任何一个杯子自然挥发干净的时间为b。
// 四个参数:arr, n, a, b
// 假设时间点从0开始,返回所有人喝完咖啡并洗完咖啡杯的全部过程结束后,至少来到什么时间点。
// 验证的方法// 彻底的暴力// 很慢但是绝对正确public static int right(int[] arr, int n, int a, int b) {int[] times = new int[arr.length];int[] drink = new int[n];return forceMake(arr, times, 0, drink, n, a, b);}// 每个人暴力尝试用每一个咖啡机给自己做咖啡public static int forceMake(int[] arr, int[] times, int kth, int[] drink, int n, int a, int b) {if (kth == n) {int[] drinkSorted = Arrays.copyOf(drink, kth);Arrays.sort(drinkSorted);return forceWash(drinkSorted, a, b, 0, 0, 0);}int time = Integer.MAX_VALUE;for (int i = 0; i < arr.length; i++) {int work = arr[i];int pre = times[i];drink[kth] = pre + work;times[i] = pre + work;time = Math.min(time, forceMake(arr, times, kth + 1, drink, n, a, b));drink[kth] = 0;times[i] = pre;}return time;}public static int forceWash(int[] drinks, int a, int b, int index, int washLine, int time) {if (index == drinks.length) {return time;}// 选择一:当前index号咖啡杯,选择用洗咖啡机刷干净int wash = Math.max(drinks[index], washLine) + a;int ans1 = forceWash(drinks, a, b, index + 1, wash, Math.max(wash, time));// 选择二:当前index号咖啡杯,选择自然挥发int dry = drinks[index] + b;int ans2 = forceWash(drinks, a, b, index + 1, washLine, Math.max(dry, time));return Math.min(ans1, ans2);}// 以下为贪心+优良暴力public static class Machine {public int timePoint;public int workTime;public Machine(int t, int w) {timePoint = t;workTime = w;}}public static class MachineComparator implements Comparator<Machine> {@Overridepublic int compare(Machine o1, Machine o2) {return (o1.timePoint + o1.workTime) - (o2.timePoint + o2.workTime);}}// 优良一点的暴力尝试的方法public static int minTime1(int[] arr, int n, int a, int b) {PriorityQueue<Machine> heap = new PriorityQueue<Machine>(new MachineComparator());for (int i = 0; i < arr.length; i++) {heap.add(new Machine(0, arr[i]));}int[] drinks = new int[n];for (int i = 0; i < n; i++) {Machine cur = heap.poll();cur.timePoint += cur.workTime;drinks[i] = cur.timePoint;heap.add(cur);}return bestTime(drinks, a, b, 0, 0);}// drinks 所有杯子可以开始洗的时间// wash 单杯洗干净的时间(串行)// air 挥发干净的时间(并行)// free 洗的机器什么时候可用// drinks[index.....]都变干净,最早的结束时间(返回)public static int bestTime(int[] drinks, int wash, int air, int index, int free) {if (index == drinks.length) {return 0;}// index号杯子 决定洗int selfClean1 = Math.max(drinks[index], free) + wash;int restClean1 = bestTime(drinks, wash, air, index + 1, selfClean1);int p1 = Math.max(selfClean1, restClean1);// index号杯子 决定挥发int selfClean2 = drinks[index] + air;int restClean2 = bestTime(drinks, wash, air, index + 1, free);int p2 = Math.max(selfClean2, restClean2);return Math.min(p1, p2);}// 贪心+优良尝试改成动态规划public static int minTime2(int[] arr, int n, int a, int b) {PriorityQueue<Machine> heap = new PriorityQueue<Machine>(new MachineComparator());for (int i = 0; i < arr.length; i++) {heap.add(new Machine(0, arr[i]));}int[] drinks = new int[n];for (int i = 0; i < n; i++) {Machine cur = heap.poll();cur.timePoint += cur.workTime;drinks[i] = cur.timePoint;heap.add(cur);}return bestTimeDp(drinks, a, b);}public static int bestTimeDp(int[] drinks, int wash, int air) {int N = drinks.length;int maxFree = 0;for (int i = 0; i < drinks.length; i++) {maxFree = Math.max(maxFree, drinks[i]) + wash;}int[][] dp = new int[N + 1][maxFree + 1];for (int index = N - 1; index >= 0; index--) {for (int free = 0; free <= maxFree; free++) {int selfClean1 = Math.max(drinks[index], free) + wash;if (selfClean1 > maxFree) {break; // 因为后面的也都不用填了}// index号杯子 决定洗int restClean1 = dp[index + 1][selfClean1];int p1 = Math.max(selfClean1, restClean1);// index号杯子 决定挥发int selfClean2 = drinks[index] + air;int restClean2 = dp[index + 1][free];int p2 = Math.max(selfClean2, restClean2);dp[index][free] = Math.min(p1, p2);}}return dp[0][0];}