【声明】
内容源自网络,版权归原作者!
【自序】
费曼说没人理解量子力学。 量子力学是门科学不是玄学,是一大批物理大师共同创立的,我们生活中无时无刻都在用他,未来科技发展方向。因此闲暇之余浅尝辄止的学习算是与时俱进,谨立此手账,以褒其行,彰其德,昭于后琨也。
一、量子力学、量子场论
【量子力学】
量子力学是描写原子和亚原子尺度的物理学理论。19世纪末,经典力学和经典电动力学在描述微观系统时的不足越来越明显。量子力学是在20世纪初由马克斯·普朗克、尼尔斯·玻尔、沃纳·海森堡、埃尔温·薛定谔、沃尔夫冈·泡利、路易·德布罗意、马克斯·玻恩、恩里科·费米、保罗·狄拉克、阿尔伯特·爱因斯坦、康普顿等一大批物理学家共同创立的。

“1927年第五届索尔维会议合照”
此图乃「量子学派」修复绝版高清彩照

此图乃「量子学派」花了三个月时间精心搜集整理
在量子力学中,一个物理体系的状态由波函数表示,波函数的任意线性叠加仍然代表体系的一种可能状态。对应于代表该量的算符对其波函数的作用;波函数的模平方代表作为其变量的物理量出现的概率密度。
叠加态是“ 0” 态和“ 1” 态的任意线性叠加,它既可以是“ 0” 态又可以是“ 1” 态,“ 0” 态和“ 1” 态各以一定的概率同时存在. 通过测量或与其它物体发生相互作用而呈现出“ 0” 态或 “ 1” 态.任何两态的量子系统都可用来实现量子位,例如氢原子中的电子的基态(ground state)和第 1 激发态(first excited state)、 质子自旋在任意方向的+ 1/ 2 分量和- 1/ 2 分量、 圆偏振光的左旋和右旋等。
一个量子系统包含若干粒子,这些粒子按照量子力学的规律运动,称此系统处于态空间的某种量子态。这里所说的态空间是指由多个本征态(eigenstate) (即基本的量子态)所张成的矢量空间,基本量子态简称基本态(basic state)或基矢(basic vector) . 态空间可用Hilbert 空间(线性复向量空间)来表述,即Hilbert 空间可以表述量子系统的各种可能的量子态.为了便于表示和运算,Dirac提出用符号|x〉 来表示量子态,|x〉 是一个列向量,称为ket ;它的共轭转置(conjugate t ranspose) 用〈x|表示,〈x|是一个行向量,称为bra.一个量子位的叠加态可用二维Hilbert 空间(即二维复向量空间)的单位向量来描述。

公式配图: 百度百科截图
【量子场论】
量子场论(Quantum Field Theory, QFT),是量子力学狭义相对论和经典场论相结合的物理理论,已被广泛的应用于粒子物理学和凝聚态物理学中。量子场论为描述多粒子系统,尤其是包含粒子产生和湮灭过程的系统,提供了有效的描述框架。量子场论的最初建立历程是和量子力学以及狭义相对论密不可分的,它是基本粒子物理标准模型的理论框架。
量子场论的建立基于经典场论,狭义相对论和量子力学。经典场的物理性质可以用一些定义在全空间的量描述〔例如电磁场的性质可以用电场强度和磁场强度或用一个三维矢量势A(x,t)和一个标量势\phi(x,t)描述〕。这些场量是空间坐标和时间的函数,它们随时间的变化描述场的运动。空间不同点的场量可以看作是互相独立的动力学变量,因此场是具有连续无穷维自由度的系统。场论是关于场的性质、相互作用和运动规律的理论。量子场论则是在量子力学基础上建立和发展的场论,即把量子力学原理应用于场,把场看作无穷维自由度的力学系统实现其量子化而建立的理论。量子场论是粒子物理学的基础理论,但也被广泛地应用于核理论和凝聚态理论等近代物理学的其他许多分支。
【量子状态】
参考:《你完全可以理解量子信息(4-5)》
公众号:风云之声 2017-10-10
作者:袁岚峰
~~~ ~~~
用一种数学符号表示量子力学中的状态,就是在一头竖直一头尖的括号“|>”中填一些表示状态特征的字符。这种符号是英国物理学家狄拉克发明的,称为“狄拉克符号”。在量子信息中,经常把两个基本状态写成|0>和|1>。而|0>和|1>的线性叠加,就是a|0> + b|1>,其中a和b是两个数。“线性”意味着用一个数乘以一个状态,“叠加”意味着两个状态相加,所以“线性叠加”就是把两个状态各自乘以一个数后再加起来。叠加原理说的是:如果一个体系能够处于|0>和处于|1>,那么它也能处于任何一个a|0> + b|1>,这样的状态称为“叠加态”。这里a和b可以取任何数,对它们唯一的限制,就是它们的绝对值的平方和等于1,即|a|2+ |b|2 = 1。在叠加原理的框架下,经典的比特变成了“ 量子比特 ”。也就是说,这个体系的状态不是只能取“0”或取“1”了,而是可以取任意的a|0>+ b|1>状态,例如(|0> + |1>)/√2、(|0> - |1>)/√2、(|0> + √3|1>)/2、(√3|0> - |1>)/2等等。从两个选择到无穷多个选择,这是个巨大的扩展。显然,一个量子比特包含比一个经典比特大得多的信息量。
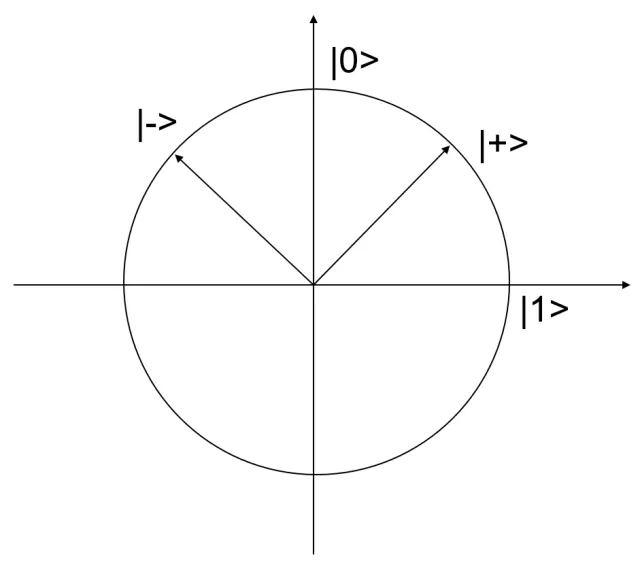
叠加原理和基组 态矢量 单位圆
我们可以定义两个状态|+> =(|0> + |1>)/√2和|-> = (|0> - |1>)/√2,相当于把|1>和|0>向左旋转45度。如果把|+>和|->当作基本状态,用它们的线性叠加来表示单位圆上所有的状态,同样是可行的,相当于把坐标系向左旋转了45度。在这个新的坐标系下,|0> = (|+> + |->)/√2,|1> = (|+> - |->)/√2。一种常见的实现量子比特的方法,就是用光子的“ 偏振态 ”。光是一种电磁波,不断地产生电场和磁场。如果电场位于某个确定的方向,我们就说这个光子是偏振的。四个状态|0>、|1>、|+>和|->,分别对应光子的偏振处于0度、90度、45度和135度。
二、量子通信
量子通信是利用量子叠加态和纠缠效应进行信息传递的新型通信方式,基于量子力学中的不确定性、测量坍缩和不可克隆三大原理提供了无法被窃听和计算破解的绝对安全性保证,主要分为量子隐形传态和量子密钥分发两种。

量子信息学科内容
配图源自公众号:风云之声 袁岚峰
【量子隐形传态】
1993年设计出来的一种实验方案,把粒子A的量子状态传输给远处的粒子B,让粒子B的状态变成粒子A最初的状态。请注意,传的是状态而不是粒子本身,两个粒子的空间位置都没有变化,没有传送实际粒子,不是超光速传输。

图片来源 | 跨越鸿沟 谢春生 量子计算50页PPT
【量子密码术】
香农定理(香农证明的)绝对安全三个条件:
一,密钥是一串随机的字符串;二,密钥的长度跟明文一样,甚至更长;三,每传送一次密文就更换密钥,即“一次一密”。长度跟明文相等、随机、一次一密,满足这 3 个条件的密钥叫作“一次性便笺”。因此,密码学中一个重要的定理就是:用一次性便笺加密的密文,是绝对不可破译的。这条定理是信息论的创始人克劳德·香农证明的。量子密码术利用了量子力学中的两个原理,一个是叠加原理,另一个是测量可能导致状态突变。基于这两个原理,通过发射和接收一系列处于随机状态的单光子,来使通信双方获得一串相同的随机字符串。这串随机字符串就是一次性便笺密钥。
量子密码术的安全性表现在五个方面: 一,密文即使被截获了也不会被破译;二,不会被计算技术的进步破解;三,没有传递密钥的信使;四,可以在每次使用前现场产生密钥,平时不需要保存密钥;五,在密钥生成过程中如果有人窃听,会被通信方发现。
人们说量子密码具有绝对安全性,意思是指量子密码不可能用数学方法破解,要窃密只能用物理方法攻击设备。在对传统密码的破解中,主要考虑数学破解,是因为用数学就“有可能”破解它们,而不是“只有”用数学才能破解它们。量子密码术和传统密码术的对比,是量子密码术面临的威胁只来自物理,传统密码术面临的威胁来自数学加物理!也就是说,只要量子通信设备是可靠的,那么就绝对不会泄密。
量子密码术真实的做法是:用量子信道产生密钥,用传统信道传送密文。你也许想问:既然量子信道可以保证不泄密,那为什么不直接用量子信道传输信息,而只是传输密钥呢?因为这种量子力学的操作只能产生随机字符串,随机字符串的信息量是零,所以这种操作本身不能传输信息。因此,这种方法的提出者在很长时间内想不出它有什么用,直到发现这段随机字符串可以作密钥,才让这种方法有了用武之地。
Kim注:
量子密码术中量子密钥分发只需要单光子线性叠加和测量,不涉及多光子纠缠(很意外)。满足香农定理绝对安全(无条件安全)定义:采用对称加密(重点,之前没有想到),没有信使传递密钥,密钥长度大于等于明文长度,密钥随机选取,不受算力技术进步制约,通信接收方公布接收内容,发送方回复核对结果,能够及时发现是否被窃听或破坏,不用保护全部线路节点,不依耐数学难题。
【量子密钥分发】
京沪干线,全光中继 :key1、key2…keyN分段加密接力,类似暗网洋葱加密,不是将光子的功率放大。
墨子号:自由空间传输密钥,针尖对麦芒,对准需要很高的精度,密钥光子肉眼看不见,能看见的是信标。
【BB84通讯协议】

配图来源 微信公众号:科工力量
密钥(Key)产生的关键步骤:接收方通过公开信道(电子邮件或电话)把自己使用的偏振滤色片的序列告知发送方,发送方把接收方滤色片的序列与自己使用的序列逐一对照,然后告知接收方哪几次用了正确的滤色片(打勾️的1,4,5,7,9)。对应于这些用了正确滤色片后接收到的光子状态的代码是:00110,接发双方对此都心知肚明、毫无疑义,这组代码就是它们两人共享的密钥。
|0>

|1>

|2>

图片来源 | 跨越鸿沟 谢春生 量子计算50页PPT
诱骗态协议:实际光通讯协议,解决多光子通讯窃听问题。实际系统中单光子源难以制备,通常使用的是弱相干光源,通过将激光光源衰减后获得。弱相干光源的光子数分布服从泊松分布,其中存在不可忽略的多光子成分。对于多光子成分,Eve 可以采取光子数分离(photon-number splitting,PNS)攻击来窃听。
三、量子计算
量子位(qubit)是量子计算的理论基石。在常规计算机中,信息单元用二进制的 1 个位来表示,它不是处于“ 0” 态就是处于“ 1” 态. 在二进制量子计算机中,信息单元称为量子位,它除了处于“ 0” 态或“ 1” 态外,还可处于叠加态(superposed state)。
量子力学态叠加原理使得量子信息单元的状态可以处于多种可能性的叠加状态,从而导致量子信息处理从效率上相比于经典信息处理具有更大潜力。普通计算机中的2位寄存器在某一时间仅能存储4个二进制数(00、01、10、11)中的一个,而量子计算机中的2位量子位(qubit)寄存器可同时存储这四种状态的叠加状态。随着量子比特数目的增加,对于n个量子比特而言,量子信息可以处于2种可能状态的叠加,配合量子力学演化的并行性,可以展现比传统计算机更快的处理速度。
把量子考虑成磁场中的电子。电子的旋转可能与磁场一致,称为上旋转状态,或者与磁场相反,称为下旋状态。如果我们能在消除外界影响的前提下,用一份能量脉冲能将下自旋态翻转为上自旋态;那么,我们用一半的能量脉冲,将会把下自旋状态制备到一种下自旋与上自旋叠加的状态上(处在每种状态上的几率为二分之一)。对于n个量子比特而言,它可以承载2的n次方个状态的叠加状态。而量子计算机的操作过程被称为幺正演化,幺正演化将保证每种可能的状态都以并行的方式演化。这意味着量子计算机如果有500个量子比特,则量子计算的每一步会对2^500种可能性同时做出了操作。
量子计算机能够快速处理大数分解、密码破解、搜索、优化等问题,目前是通过量子计算模拟器在传统的超级计算机上模拟量子计算机,对于量子计算算法研究,具有重要支撑作用。
【量子退相干】
在量子力学里,开放量子系统的量子相干性会因为与外在环境发生量子纠缠而随着时间逐渐丧失,这效应称为量子退相干(英语:Quantum decoherence),又称为量子去相干。量子退相干是量子系统与环境因量子纠缠而产生的后果。由于量子相干性而产生的干涉现象会因为量子退相干而变得消失无踪。量子退相干促使系统的量子行为变迁成为经典行为,这过程称为“量子至经典变迁”(quantum-to-classical transition)。德国物理学者汉斯·泽贺最先于1970年提出量子退相干的概念。自1980年以来,量子退相干已成为热门研究论题。
Kim注:量子纠缠时间很短,存在噪声等随机干扰导致计算错误,需要费很大力气维持纠缠状态,会分散量子计算本身精力。
理工男神李永乐老师介绍潘建伟院士18光量子比特纠缠计算实验:
量子纠缠、叠加态并行计算:6*3=18qbit纠缠。

B站视频截图
纠缠计算实验装置:
由潘建伟、陆朝阳带领的中国科学技术大学、中国科学院-阿里巴巴量子计算实验室等机构组成的团队,完成了首个在小规模光量子处理器上进行拓扑数据分析(TDA)的概念验证演示。
研究人员表示,其实验成功展示了量子TDA算法的可行性,并且表明数据分析可能是未来量子计算的一大重要应用。
论文的第一作者是He-Liang Huang,这项验证演示以MIT的Seth Lloyd及其同事的工作为基础,Lloyd等人在2016年开发了一种量子算法,叫做拓扑数据分析(TDA),可以大大加快贝蒂数的计算速度。TDA量子算法按照n的5次方扩展,比已知的最快的经典算法速度快了好几个数量级。但是,这个研究完全是理论上的。
现在,Huang等人所做的工作是在原理验证实验中,在量子计算机上运行TDA算法。团队使用六光子量子处理器,分析了三个数据点在两个不同尺度的网络中的贝蒂数的拓扑特征。结果完全如预期。实验装置如下图:

您若看到这里,借用一下袁岚峰老师的话,您已经比99.99%的人更懂量子科学了:)
(未完待续…)
Kim 收集整理
2020.10.24

