字符串操作
题解:先变为没出现过的字符,然后在正常的变换
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** 返回满足题意的最小操作数* @param str string字符串 给定字符串* @return int整型*/int minOperations(string str) {// write code heremap<int,int>mp;for(int i=0;i<str.length();i++){mp[str[i]]++;}int num=0;int res=0;for(int i=0;i<26;i++){if(!mp[i+97]){num++;}}for(int i=0;i<26;i++){if(mp[i+97]>1){if(mp[i+97]==2){res++;}else{int x=mp[i+97];if(x%2==1){int w=x/2;if(w<num){num-=w;res+=w;}else{res+=num;res+=(x-2*num-1);num=0;}}else{int w=x/2;if(w<num){num-=w;num++;res+=w;}else{res+=num;res+=(x-2*num-1);num=0;}}}}}return res;}
};
2.
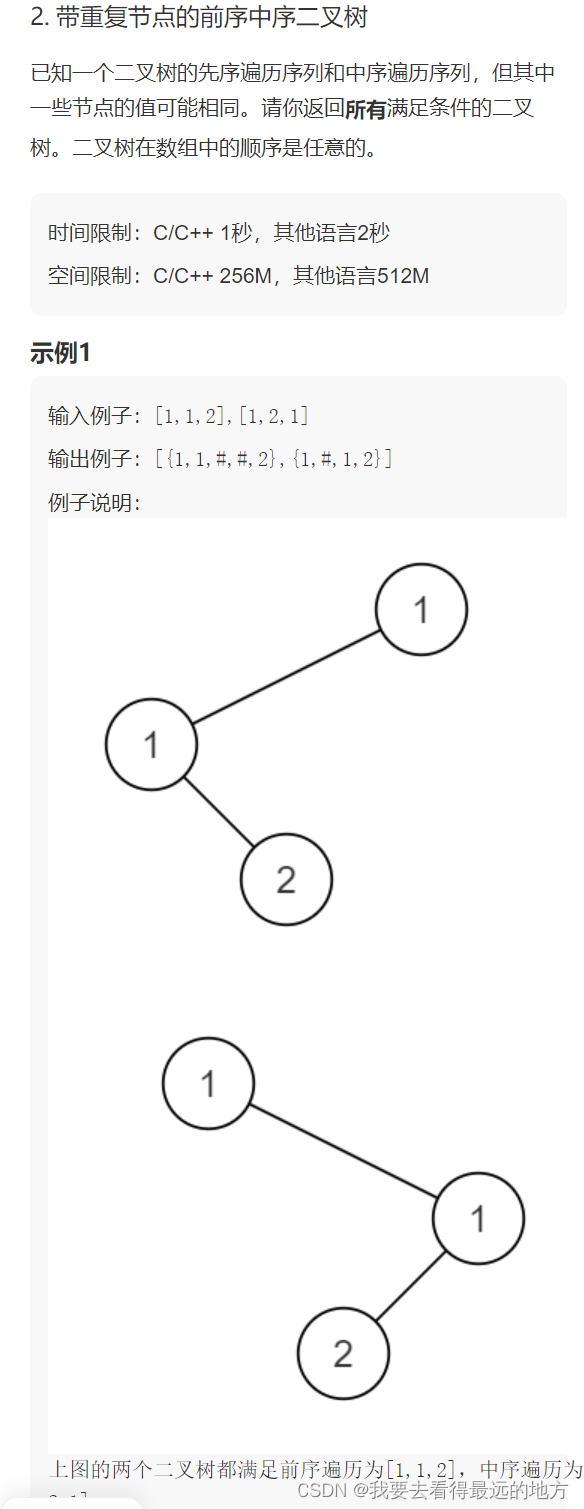
带重复节点的前序中序二叉树
递归求解,前序遍历的第一个节点将中序遍历分为左右子树
/*** struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param preOrder int整型vector * @param inOrder int整型vector * @return TreeNode类vector*/vector<TreeNode*>res;vector<TreeNode*> dfs(vector<int>& preOrder,vector<int>& inOrder,int L1,int R1,int L2,int R2){vector<TreeNode*> res;if(L1>R1){res.push_back(nullptr);return res;}int k=preOrder[L1];for(int i=L2;i<=R2;i++){int l=i-L2;if(inOrder[i]==k){vector<TreeNode*> left=dfs(preOrder,inOrder,L1+1,L1+l,L2,i-1);vector<TreeNode*> right=dfs(preOrder,inOrder,L1+1+l,R1,i+1,R2);for(TreeNode* le:left){for(TreeNode* ri:right){TreeNode* s=new TreeNode(k);// s->val=k;s->left=le;s->right=ri;res.push_back(s);}}}}return res;}vector<TreeNode*> getBinaryTrees(vector<int>& preOrder, vector<int>& inOrder) {// write code hereint pL=preOrder.size();int iL=inOrder.size();return dfs(preOrder,inOrder,0,pL-1,0,iL-1);}
}; 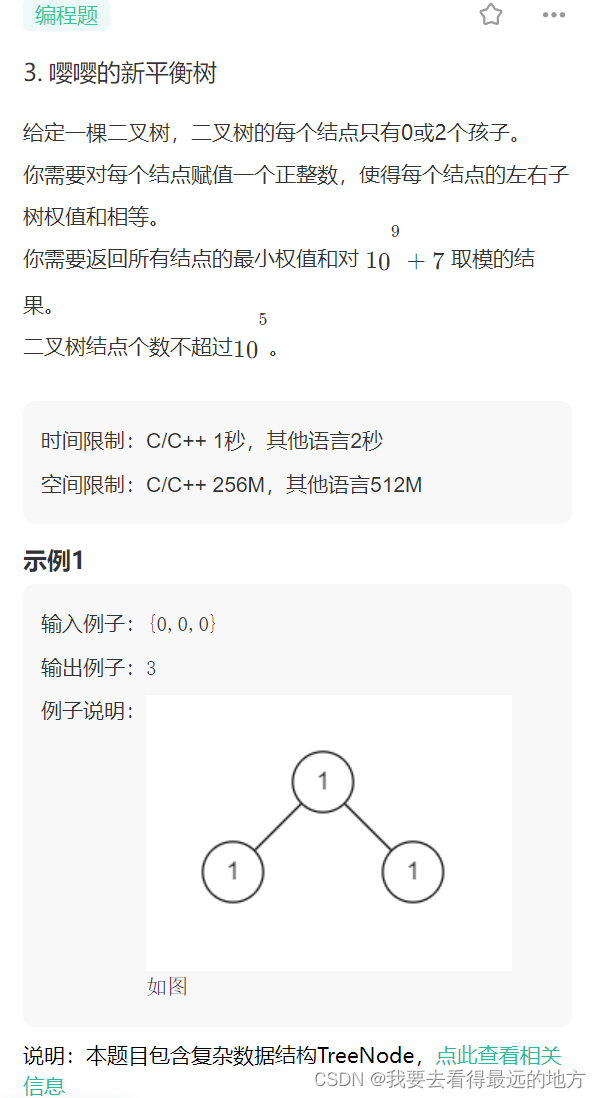
3.嘤嘤的新平衡树
刚开始用递归写的用的最小最大那种方法,因为中间取mod了所以答案不会对,最后参考网上答案发现用满二叉树这个性质。
/*** struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* };*/
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param tree TreeNode类 * @return int整型*/int mod=1e9+7;long long dfs(TreeNode* tree){long long res=1;if(tree==nullptr) return 0; if(tree->left==nullptr && tree->right==nullptr){return 1;}else{res+= max(dfs(tree->left),dfs(tree->right));}return res;}int getTreeSum(TreeNode* tree) {int n=dfs(tree);int res=1;for(int i=1;i<=n;i++){res=res*2%mod;}return res-1;}
};
01串修改
先0变1
在1变0
取两者之间操作的最小值
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param str string字符串 * @return int整型*/int minOperations(string str) {// write code hereint n=str.length();if(n==1) return 0;//0变1//同时更改两个0优先int num1=0;for(int i=0;i<=n-1;i++){if(str[i]=='0'){i++;num1++;}// else if(str[i]=='0')// {// num1++;// i++;// }}int num2=0;for(int i=0;i<=n-1;i++){if(str[i]=='1'){i++;num2++;}// else if(str[i]=='1')// {// num2++;// i++;// }}//1变0return min(num1,num2);}
}; 
5.连续子数组数量
双端滑动窗口(技巧需要计算一下在某个区间范围内的2的个数和5的个数,取最小值,即是后缀0的个个数)
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param a int整型vector * @param x int整型 * @return int整型*///滑动窗口int getSubarrayNum(vector<int>& a, int x) {// write code hereint n=a.size();vector<int>num5(n+1,0);vector<int>num2(n+1,0);int res=0;int mod=1e9+7;for(int i=0;i<n;i++){int m=a[i];while(m){int t=0;while(m%5==0&&m!=0){m=m/5;num5[i]++;t++;}while(m%2==0&&m!=0){m=m/2;num2[i]++;t++;}break;}if(i!=0){num2[i]+=num2[i-1];num5[i]+=num5[i-1];} }int l=0;for(int i=0;i<n;i++){int x2;int x5;if(l==0){x2=num2[i];x5=num5[i];}else{x2=num2[i]-num2[l-1];x5=num5[i]-num5[l-1];}int k=min(x2,x5);if(k>=x){res+=(n-i);res=res%mod;int L1=l;while(l<=i && k>=x){l++;x2=num2[i]-num2[l-1];x5=num5[i]-num5[l-1];k=min(x2,x5);}res+=(l-L1-1)*(n-i)%mod;}}return res;}
};
6.好矩阵
不会(搜的答案是先确定第一行和第一列然后其他就奇偶性就确定了)
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param n int整型 * @param m int整型 * @param x int整型 * @return int整型*/// int mod = 1e9 + 7;// /*// * 封装的快速幂// */// int power(int a, long long b) {// int res = 1;// while (b) {// if (b & 1)res = 1LL * res * a % mod;// b >>= 1;// a = 1LL * a * a % mod;// }// return res;// }// int numsOfGoodMatrix(int n, int m, int x) {// return 1LL * power(x, n + m - 1) * power(x / 2, 1LL * (n - 1) * (m - 1)) % mod;// }int mod=1e9+7;int ksm(int x,long long h){long long res=1;while(h>0){if(h&1){res=res*x;res=res%mod;// cout<<res<<endl;}x=1LL*x*x%mod;h>>=1;}return res%mod;}int numsOfGoodMatrix(int n, int m, int x) {// write code here//快速幂return 1LL*ksm(x,m+n-1)*ksm(x/2,1LL*(m-1)*(n-1))%mod;}
};