注:在洛谷同时发布。
题目链接
解题思路
首先观察样例。似乎什么也观察不出来?
那就根据题目描述中所给的图表做。首先找到对角线,将图形沿着对角线一分为二。注意对角线上可以看到一个人,所以答案要加 1 1 1。
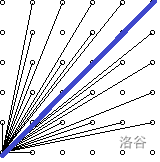
其次逐个分析。可以发现,两部分是对称的。设每两个人之间的距离为 1 1 1 ,样例就简化为一个直角边长 ( n − 1 ) (n-1) (n−1) 等腰直角三角形(不算左下角)。
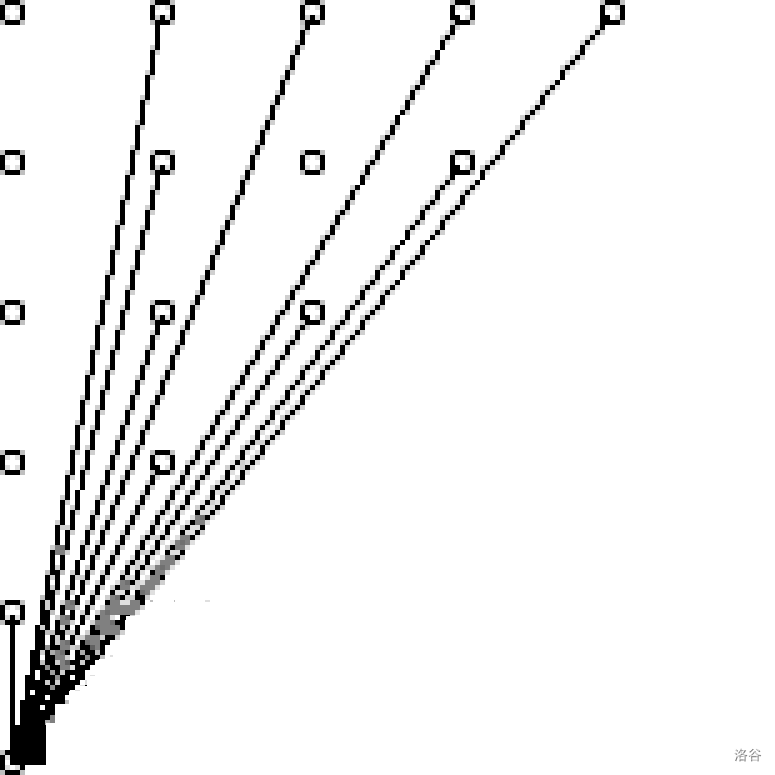
建立笛卡尔坐标系。将左下角设为 ( 0 , 0 ) (0,0) (0,0) ,这样就可以将图中的每个与 ( 0 , 0 ) (0,0) (0,0) 有边连接的点表示出来。

不难发现,除 ( 1 , 0 ) (1,0) (1,0) 外,剩下的每个与 ( 0 , 0 ) (0,0) (0,0) 有边相连的点的横坐标与纵坐标所对应的值互质。
观察每一行。可以发现,每行与 ( 0 , 0 ) (0,0) (0,0) 有边相连的点的个数正好是与横坐标相互质的数的个数,也就是 φ \varphi φ ( i ) (i) (i) 。
所以该题目就可以转化为求 2 ∑ n − 1 i = 1 2\sum_{n-1}^{i=1} 2∑n−1i=1 φ \varphi φ ( i ) + 1 (i)+1 (i)+1
但为了保证严谨,第 1 1 1 行的 ( 1 , 0 ) (1,0) (1,0) 一般单独处理。
则该题目被转化为求 2 ∑ n − 1 i = 2 2\sum_{n-1}^{i=2} 2∑n−1i=2 φ \varphi φ ( i ) + 3 (i)+3 (i)+3
代码实现
前置知识:试除法求 φ \varphi φ ( i ) (i) (i)
inline int phi(int x)
{int ret=x;for(int i=2;i*i<=x;++i){if(x%i==0){ret=ret/i*(i-1);while(x%i==0)x/=i;}}if(x>1)ret=ret/x*(x-1);return ret;
}
首先 1 → \rightarrow →n-1 (或 2 → \rightarrow →n-1) 扫一遍。然后再用试除法(时间复杂度 n \sqrt n n ) 求出 φ \varphi φ ( i ) (i) (i) ,将其累加起来就解决了。
最后注意要加上对角线一行的 1 (或 3)!
但是当 n = 1 n=1 n=1 时,由于 ( 0 , 0 ) (0,0) (0,0) 无法被看到(自己不能看到自己),所以答案是 0 0 0
时间复杂度 O ( n n ) O(n \sqrt n) O(nn) ,可以轻而易举的通过测试。
AC代码
当求 2 ∑ n − 1 i = 2 2\sum_{n-1}^{i=2} 2∑n−1i=2 φ \varphi φ ( i ) + 3 (i)+3 (i)+3 时
#include<bits/stdc++.h>
using namespace std;
int n,ans=0;
inline int phi(int x)//试除法求欧拉函数
{int ret=x;for(int i=2;i*i<=x;++i){if(x%i==0){if(x%i==0){while(x%i==0)x/=i;ret=ret/i*(i-1);}}}if(x>1)ret=ret/x*(x-1);return ret;
}
signed main()
{cin>>n;if(n==1)puts("0"),exit(0);//特判,也可写作N<2for(int i=2;i<n;++i)ans+=phi(i);//统计答案cout<<ans*2+3;return 0;
}
当求 2 ∑ n − 1 i = 1 2\sum_{n-1}^{i=1} 2∑n−1i=1 φ \varphi φ ( i ) + 1 (i)+1 (i)+1 时
#include<bits/stdc++.h>
using namespace std;
int n,ans=0;
inline int phi(int x)//试除法
{int ret=x;for(int i=2;i*i<=x;++i){if(x%i==0){if(x%i==0){while(x%i==0)x/=i;ret=ret/i*(i-1);}}}if(x>1)ret=ret/x*(x-1);return ret;
}
signed main()
{cin>>n;if(n==1)puts("0"),exit(0);//特判for(int i=1;i<=n-1;++i)ans+=phi(i);//统计答案cout<<ans*2+1;return 0;
}
拓展题目
如果你通过了这道题,你还可以试试这些题目:
[SDOI2012] Longge 的问题
[SDOI2008] 沙拉公主的困惑