NumPy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
NumPy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发,2005 年,Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色,并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。
NumPy 是一个运行速度非常快的数学库,主要用于数组计算,包含:
- 一个强大的N维数组对象 ndarray
- 广播功能函数
- 整合 C/C++/Fortran 代码的工具
- 线性代数、傅里叶变换、随机数生成等功能
目录
numpy%E5%BA%94%E7%94%A8-toc" style="margin-left:0px;">1.numpy应用
numpy%E5%AF%B9%E8%B1%A1-toc" style="margin-left:0px;">2.numpy对象
3.一维数组
3.1 间隔索引
3.2 布尔索引
3.3 其余方法
4.二维数组
4.1. 创建二维数组
4.2.二维数组的数据读取
编辑4.3.二位数组的常见属性
4.4.常用函数
4.4.1.比较函数
4.4.2.数学函数
4.4.3.统计函数
5.线性代数
numpy.dot()-toc" style="margin-left:40px;">numpy.dot()
numpy.vdot()-toc" style="margin-left:40px;">numpy.vdot()
numpy.inner()-toc" style="margin-left:40px;">numpy.inner()
numpy.matmul-toc" style="margin-left:40px;">numpy.matmul
numpy.linalg.det()-toc" style="margin-left:40px;">numpy.linalg.det()
numpy.linalg.solve()-toc" style="margin-left:40px;">numpy.linalg.solve()
numpy.linalg.inv()-toc" style="margin-left:40px;">numpy.linalg.inv()
6.文件读写(OI)
7.ndarray形状操作
7.1. 改变 ndarray 数组形状
7.2. 将不同数组堆叠在一起
7.3. 将一个数组拆分成几个较小的数组
numpy%E5%BA%94%E7%94%A8" style="background-color:transparent;">1.numpy应用
NumPy 通常与 SciPy(Scientific Python)和 Matplotlib(绘图库)一起使用, 这种组合广泛用于替代 MatLab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
SciPy 是一个开源的 Python 算法库和数学工具包。
SciPy 包含的模块有最优化、线性代数、积分、插值、特殊函数、快速傅里叶变换、信号处理和图像处理、常微分方程求解和其他科学与工程中常用的计算。
Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包,如 Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口(API)。
相关链接
- NumPy 官网 http://www.numpy.org/
- NumPy 源代码:GitHub - numpy/numpy: The fundamental package for scientific computing with Python.
- SciPy 官网:SciPy -
- SciPy 源代码:GitHub - scipy/scipy: SciPy library main repository
- Matplotlib 教程:Matplotlib 教程
- Matplotlib 官网:Matplotlib — Visualization with Python
- Matplotlib 源代码:GitHub - matplotlib/matplotlib: matplotlib: plotting with Python
numpy%E5%AF%B9%E8%B1%A1">2.numpy对象
NumPy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
ndarray 对象是用于存放同类型元素的多维数组。
ndarray 中的每个元素在内存中都有相同存储大小的区域。
ndarray 内部由以下内容组成:
-
一个指向数据(内存或内存映射文件中的一块数据)的指针。
-
数据类型或 dtype,描述在数组中的固定大小值的格子。
-
一个表示数组形状(shape)的元组,表示各维度大小的元组。
-
一个跨度元组(stride),其中的整数指的是为了前进到当前维度下一个元素需要"跨过"的字节数。
ndarray 的内部结构:

跨度可以是负数,这样会使数组在内存中后向移动,切片中 obj[::-1] 或 obj[:,::-1] 就是如此。
创建一个 ndarray 只需调用 NumPy 的 array 函数即可:
numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)参数说明:
| 名称 | 描述 |
|---|---|
| object | 数组或嵌套的数列 |
| dtype | 数组元素的数据类型,可选 |
| copy | 对象是否需要复制,可选 |
| order | 创建数组的样式,C为行方向,F为列方向,A为任意方向(默认) |
| subok | 默认返回一个与基类类型一致的数组 |
| ndmin | 指定生成数组的最小维度 |
接下来可以通过以下实例帮助我们更好的理解。
实例 1
import numpy as np a = np.array([1,2,3]) print (a)输出结果如下:
[1 2 3]
实例 2
# 多于一个维度
import numpy as npa = np.array([[1, 2], [3, 4]])print (a)输出结果如下:
[[1 2] [3 4]]
实例 3
# 最小维度
import numpy as np
a = np.array([1, 2, 3, 4, 5], ndmin = 2)print (a)输出如下:
[[1 2 3 4 5]]
实例 4
# dtype 参数
import numpy as np
a = np.array([1, 2, 3], dtype = complex)
print (a)输出结果如下:
[1.+0.j 2.+0.j 3.+0.j]
ndarray 对象由计算机内存的连续一维部分组成,并结合索引模式,将每个元素映射到内存块中的一个位置。内存块以行顺序(C样式)或列顺序(FORTRAN或MatLab风格,即前述的F样式)来保存元素。
3.一维数组
数组还有列表没有的索引方法
3.1 间隔索引
b=list(range(10))
b_array=np.array(b)
print(b_array[[1,2,3]])
print(b[[1,2,3]])运行结果可以清楚的看到对于列表 b 提示“TypeError: list indices must be integers or slices, not list”,而对于一维数组 b_array 通过[[index1,index2...]]的方式,实现了多数值间隔索引。
[1 2 3]
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-12-d90ec075f85c> in <module>
2 b_array=np.array(b)
3 print(b_array[[1,2,3]])
----> 4 print(b[[1,2,3]])TypeError: list indices must be integers or slices, not list
3.2 布尔索引
布尔索引,又叫逻辑索引,可以很快很方便的实现对数据进行判断,代码简洁。
b=list(range(10))
b_array=np.array(b)
print("*"*40)
#找出b_array中小于5的数字
print(b_array <5) # 形成布尔值
print(b_array[b_array <5 ]) # 按照布尔值选出值
print("*"*40)#找出奇数
print(b_array%2 == 1)# 形成布尔值
print(b_array[b_array%2 == 1]) # 按照布尔值选出值
#运行结果:
****************************************
[ True True True True True False False False False False]
[0 1 2 3 4]
****************************************
[False True False True False True False True False True]
[1 3 5 7 9]
3.3 其余方法
a 作为列表有如下方法
而 a_array 有如下方法

我们先看看常用属性吧
以下是一维数组(ndarray)的方法和属性表格,包含参数及其说明:
| 方法/属性 | 参数 | 说明 |
|---|---|---|
all() | 无 | 如果数组中的所有元素都为 True,则返回 True,否则返回 False。 |
any() | 无 | 如果数组中至少有一个元素为 True,则返回 True,否则返回 False。 |
argmax() | axis(可选) | 返回数组中最大值的索引。 |
argmin() | axis(可选) | 返回数组中最小值的索引。 |
ndim | 无 | 数组的维度数量(秩)。 |
shape | 无 | 数组的形状,即每个维度的大小。 |
size | 无 | 数组中元素的总数。 |
dtype | 无 | 数组元素的类型。 |
itemsize | 无 | 数组中每个元素的字节大小。 |
flags | 无 | 数组的内存信息,如是否是连续的、是否可以写入等。 |
real | 无 | 数组元素的实部(对于复数数组)。 |
imag | 无 | 数组元素的虚部(对于复数数组)。 |
import numpy as npb_array = np.array(range(0, 10))
print(b_array)
print(b_array.all()) # 判断b_array 每个值是否是True
print(b_array.any()) # 判断b_array 任意一个值是否是True,是的话为True
print(b_array.argmax()) # 最大参数
print(b_array.argmin()) # 最小参数print("*" * 50)
print(b_array.ndim) # 秩,即轴的数量或维度的数量
print(b_array.shape) # 数组的维度,对于矩阵,n 行 m 列
print(b_array.size) # 数组元素的总个数,相当于 .shape 中 n*m 的值print("*" * 50)
print(b_array.dtype) # ndarray 对象的元素类型
print(b_array.itemsize) # ndarray 对象中每个元素的大小,以字节为单位
print(b_array.flags) # ndarray 对象的内存信息print("*" * 50)
print(b_array.real) # ndarray 元素的实部
print(b_array.imag) # ndarray 元素的虚部运行结果
[0 1 2 3 4 5 6 7 8 9]
False
True
9
0
**************************************************
1
(10,)
10
**************************************************
int32
4C_CONTIGUOUS : TrueF_CONTIGUOUS : TrueOWNDATA : TrueWRITEABLE : TrueALIGNED : TrueWRITEBACKIFCOPY : False
**************************************************
[0 1 2 3 4 5 6 7 8 9]关于属性 flags 有如下不同的分类:
属性 描述
C_CONTIGUOUS (C) 数据是在一个单一的C风格的连续段中
F_CONTIGUOUS (F) 数据是在一个单一的Fortran风格的连续段中
OWNDATA (O) 数组拥有它所使用的内存或从另一个对象中借用它
WRITEABLE (W) 数据区域可以被写入,将该值设置为 False,则数据为只读
ALIGNED (A) 数据和所有元素都适当地对齐到硬件上
UPDATEIFCOPY (U) 这个数组是其它数组的一个副本,当这个数组被释放时,原数组的内容将被更新
————————————————
4.二维数组
二维数组不就是矩阵,在机器学习中用的最多!!!!正对大部分数据集,及表格呗,
4.1. 创建二维数组
- 1.列表、元组转换
同一维数组,二维数组也可以从列表和元组转换而来。
# 基于嵌套列表创建二维数组
import numpy as nparr1 = np.array([[1,3,5,7],[2,4,6,8],[11,13,15,17],[12,14,16,18],[100,101,102,103]])# 基于嵌套元组创建二维数组
arr2 = np.array(((8.5,6,4.1,2,0.7),(1.5,3,5.4,7.3,9),(3.2,3,3.8,3,3),(11.2,13.4,15.6,17.8,19)))# 二维数组的打印结果
print(arr1,'\n')
print(arr2)运行结果是

- 2.使用 numpy.empty
也可以使用numpy.empty来创建一个指定形状(shape)、数据类型(dtype)且未初始化的数组
格式如
numpy.empty(shape, dtype = float, order = 'C')shape, 即数组形状
dtype ,指 数据类型,可以选择
order,有"C"和"F"两个选项,分别代表,行优先和列优先,在计算机内存中的存储元素的顺序。
代码段如下:
# 基于嵌套列表创建二维数组
import numpy as npnew_array=np.empty([2,3],int)
print(new_array)
new_array=np.empty([2,3],bool)
print(new_array)
new_array=np.empty([2,3],complex)
print(new_array)运行结果如下:

#数据是随机的,因为没有初始化
也可以使用 numpy.zeros 来创建指定大小的数组,数组元素以 0 来填充:
代码段如下:
# 基于嵌套列表创建二维数组
import numpy as npnew_array=np.zeros([4,5],dtype=int)
print(new_array)
new_array=np.zeros([2,4],dtype=bool)
print(new_array)
new_array=np.zeros([2,4],dtype=complex)
print(new_array)
类似的 numpy.ones 创建指定形状的数组,数组元素以 1 来填充,就不再赘述了
4.2.二维数组的数据读取
- a) 在二维数组中,位置索引必须写成[rows,cols]的形式,方括号的前半部分用于锁定二 维数组的行索引,后半部分用于锁定数组的列索引;
- b) 如果需要获取二维数组的所有行或列元素,那么,对应的行索引或列索引需要用英文 状态的冒号表示;
# 基于嵌套列表创建二维数组
import numpy as nparr1 = np.array([[1,3,5,7],[2,4,6,8],[11,13,15,17],[12,14,16,18],[100,101,102,103]])
print(arr1,'\n')
print(arr1[1]) # 选择出第二行
print(arr1[1,2]) # 选择出第二行,第三列的数据
print(arr1[1,:]) # 选择出第二行
print(arr1[:,3]) # 选择出第四列
print(arr1[:,[2,3]]) # 选择出第三、四列(间隔索引)

4.3.二位数组的常见属性
| 方法/属性 | 参数 | 说明 |
|---|---|---|
all() | axis(可选) | 如果数组在指定轴上的所有元素都为 True,则返回 True,否则返回 False。如果没有指定轴,则在所有元素上操作。 |
any() | axis(可选) | 如果数组在指定轴上至少有一个元素为 True,则返回 True,否则返回 False。如果没有指定轴,则在所有元素上操作。 |
argmax() | axis(可选) | 返回指定轴上最大值的索引。如果没有指定轴,则在整个数组上操作。 |
argmin() | axis(可选) | 返回指定轴上最小值的索引。如果没有指定轴,则在整个数组上操作。 |
ndim | 无 | 数组的维度数量(秩)。 |
shape | 无 | 数组的形状,即每个维度的大小(例如,对于一个矩阵,返回 n 行 m 列)。 |
size | 无 | 数组中元素的总数,相当于 .shape 中 n*m 的值。 |
dtype | 无 | 数组元素的类型。 |
itemsize | 无 | 数组中每个元素的字节大小。 |
sum() | axis(可选) | 返回数组在指定轴上的元素之和。如果没有指定轴,则在整个数组上操作。 |
mean() | axis(可选) | 返回数组在指定轴上的元素平均值。如果没有指定轴,则在整个数组上操作。 |
std() | axis(可选) | 返回数组在指定轴上的元素标准差。如果没有指定轴,则在整个数组上操作。 |
var() | axis(可选) | 返回数组在指定轴上的元素方差。如果没有指定轴,则在整个数组上操作。 |
min() | axis(可选) | 返回数组在指定轴上的最小值。如果没有指定轴,则在整个数组上操作。 |
max() | axis(可选) | 返回数组在指定轴上的最大值。如果没有指定轴,则在整个数组上操作。 |
cumsum() | axis(可选) | 返回数组在指定轴上的累积和。如果没有指定轴,则在整个数组上操作。 |
cumprod() | axis(可选) | 返回数组在指定轴上的累积积。如果没有指定轴,则在整个数组上操作。 |
运行结果为
True
True
19
0
**************************************************
2
(5, 4)
20
**************************************************
int32
4C_CONTIGUOUS : TrueF_CONTIGUOUS : FalseOWNDATA : TrueWRITEABLE : TrueALIGNED : TrueWRITEBACKIFCOPY : False
**************************************************
[[ 1 3 5 7][ 2 4 6 8][ 11 13 15 17][ 12 14 16 18][100 101 102 103]]
[[0 0 0 0][0 0 0 0][0 0 0 0][0 0 0 0][0 0 0 0]]
1.numpy.matlib.identity()
numpy.matlib.identity() 函数返回给定大小的单位矩阵。
单位矩阵是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为 1,除此以外全都为 0。
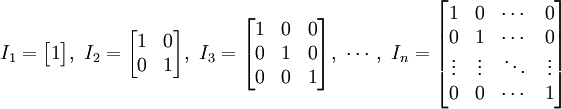
4.4.常用函数
4.4.1.比较函数

#创建两个 ndarraya=np.arange(10)
b=np.array(list(range(5,15)))
print(a)
print(b)#算数比较
print(a < b )
print(a <=b )
print(a >b )
print(a >=b )
print(a != b)
print(a == b)
print(np.less(a,b))
print(np.less_equal(a,b))
print(np.greater(a,b))
print(np.greater_equal(a,b))
print(np.not_equal(a,b))
print(np.equal(a,b))
4.4.2.数学函数
| 函数 | 函数说明 |
|---|---|
| np.round(arr) | 对各元素四舍五入 |
| np.sqrt(arr) | 计算各元素的算术平方根 |
| np.square(arr) | 计算各元素的平方值 |
| np.exp(arr) | 计算以 e 为底的指数 |
| np.power(arr, a) | 计算各元素的指数(参数 a 为指数) |
| np.log2(arr) | 计算以 2 为底各元素的对数 |
| np.log10(arr) | 计算以 10 为底各元素的对数 |
| np.add(arr1,arr2) | arr1 与 arr2(或具体数值)各个元素相加 |
| np.subtract(arr1,arr2) | arr1 与 arr2(或具体数值)各个元素相减 |
| np.multiply(arr1,arr2) | arr1 与 arr2(或具体数值)各个元素相乘 |
| np.divide(arr1,arr2) | arr1 与 arr2(或具体数值)各个元素相除 |
4.4.3.统计函数
请注意下面每个函数都有一个参数 axis,即轴,轴是指数据的方向;
axis=0时,计算数组各列的统计值;
axis=1时,计算数组各行的统计值
不指定 axis,即默认时候,是对所有元素进行统计

#创建二维数组,5行6列
a=np.arange(30).reshape((5,6))
print(a)print("-"*40)
print(np.min(a)) # 没有axis参数时候,默认是对所有元素进行统计
print(np.min(a,axis=0)) # axis = 0 ,对列进行统计
print(np.min(a,axis=1)) # axis = 1 ,对行进行统计print("-"*40)
print(np.max(a))
print(np.max(a,axis=0))
print(np.max(a,axis=1))print("-"*40)
print(np.mean(a))
print(np.mean(a,axis=0))
print(np.mean(a,axis=1))print("-"*40)
print(np.sum(a))
print(np.sum(a,axis=0))
print(np.sum(a,axis=1))
5.线性代数
NumPy 提供了线性代数函数库 linalg,该库包含了线性代数所需的所有功能,可以看看下面的说明:
| 函数 | 描述 |
|---|---|
dot | 两个数组的点积,即元素对应相乘。 |
vdot | 两个向量的点积 |
inner | 两个数组的内积 |
matmul | 两个数组的矩阵积 |
determinant | 数组的行列式 |
solve | 求解线性矩阵方程 |
inv | 计算矩阵的乘法逆矩阵 |
numpy.dot()">numpy.dot()
- 两个一维的数组,计算的是这两个数组对应下标元素的乘积和(数学上称之为向量点积);
- 二维数组,计算的是两个数组的矩阵乘积;
- 多维数组,它的通用计算公式如下,即结果数组中的每个元素都是:数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和:
dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])。
numpy.dot(a, b, out=None) 参数说明:
- a : ndarray 数组
- b : ndarray 数组
- out : ndarray, 可选,用来保存dot()的计算结果
import numpy.matlib
import numpy as npa = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]])
print(np.dot(a,b))[[1*11+2*13, 1*12+2*14],[3*11+4*13, 3*12+4*14]]
numpy.vdot()">numpy.vdot()
numpy.vdot() 函数是两个向量的点积。 如果第一个参数是复数,那么它的共轭复数会用于计算。 如果参数是多维数组,它会被展开。
import numpy as np a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]]) # vdot 将数组展开计算内积
print (np.vdot(a,b)) 
numpy.inner()">numpy.inner()
numpy.inner() 函数返回一维数组的向量内积。对于更高的维度,它返回最后一个轴上的和的乘积。
import numpy as np print (np.inner(np.array([1,2,3]),np.array([0,1,0])))
# 等价于 1*0+2*1+3*0import numpy as np
a = np.array([[1,2], [3,4]]) print ('数组 a:')
print (a)
b = np.array([[11, 12], [13, 14]]) print ('数组 b:')
print (b)print ('内积:')
print (np.inner(a,b))
numpy.matmul">numpy.matmul
numpy.matmul 函数返回两个数组的矩阵乘积。
虽然它返回二维数组的正常乘积,但如果任一参数的维数大于2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。
另一方面,如果任一参数是一维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
对于二维数组,它就是矩阵乘法:
import numpy.matlib
import numpy as np a = [[1,0],[0,1]]
b = [[4,1],[2,2]]
print (np.matmul(a,b))
numpy.linalg.det()">numpy.linalg.det()
numpy.linalg.det() 函数计算输入矩阵的行列式。
行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵,它是左上和右下元素的乘积与其他两个的乘积的差。
换句话说,对于矩阵[[a,b],[c,d]],行列式计算为 ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。
import numpy as npb = np.array([[6,1,1], [4, -2, 5], [2,8,7]])
print (b)
print (np.linalg.det(b))
print (6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2))
numpy.linalg.solve()">numpy.linalg.solve()
numpy.linalg.solve() 函数给出了矩阵形式的线性方程的解。
考虑以下线性方程:
x + y + z = 62y + 5z = -42x + 5y - z = 27
可以使用矩阵表示为:
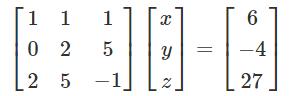
如果矩阵成为A、X和B,方程变为:
AX = B或X = A^(-1)B
import numpy as np# 定义系数矩阵 A
A = np.array([[1, 1, 1], [0, 2, 5], [2, 5, -1]])# 定义常数向量 b
b = np.array([6, -4, 27])# 使用 numpy.linalg.solve 求解线性方程组
x = np.linalg.solve(A, b)print("解为:", x) ![]()
numpy.linalg.inv()">numpy.linalg.inv()
计算矩阵的乘法逆矩阵。
逆矩阵(inverse matrix):设A是数域上的一个n阶矩阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E ,则我们称B是A的逆矩阵,而A则被称为可逆矩阵。注:E为单位矩阵。
import numpy as np x = np.array([[1,2],[3,4]])
y = np.linalg.inv(x)
print (x)
print (y)
print (np.dot(x,y))
现在创建一个矩阵A的逆矩阵:
import numpy as np a = np.array([[1,1,1],[0,2,5],[2,5,-1]]) print ('数组 a:')
print (a)
ainv = np.linalg.inv(a) print ('a 的逆:')
print (ainv)print ('矩阵 b:')
b = np.array([[6],[-4],[27]])
print (b)print ('计算:A^(-1)B:')
x = np.linalg.solve(a,b)
print (x)
# 这就是线性方向 x = 5, y = 3, z = -2 的解结果也可以使用以下函数获取:
x = np.dot(ainv,b)
6.文件读写(OI)
Numpy 可以读写磁盘上的文本数据或二进制数据。
NumPy 为 ndarray 对象引入了一个简单的文件格式:npy。
npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。
常用的 IO 函数有:
- load() 和 save() 函数是读写文件数组数据的两个主要函数,默认情况下,数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。
- savez() 函数用于将多个数组写入文件,默认情况下,数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。
- loadtxt() 和 savetxt() 函数处理正常的文本文件(.txt 等)
numpy.save()
numpy.save() 函数将数组保存到以 .npy 为扩展名的文件中。
numpy.save(file, arr, allow_pickle=True, fix_imports=True)参数说明:
- file:要保存的文件,扩展名为 .npy,如果文件路径末尾没有扩展名 .npy,该扩展名会被自动加上。
- arr: 要保存的数组
- allow_pickle: 可选,布尔值,允许使用 Python pickles 保存对象数组,Python 中的 pickle 用于在保存到磁盘文件或从磁盘文件读取之前,对对象进行序列化和反序列化。
- fix_imports: 可选,为了方便 Pyhton2 中读取 Python3 保存的数据。
import numpy as np a = np.array([1,2,3,4,5]) # 保存到 outfile.npy 文件上
np.save('outfile.npy',a) # 保存到 outfile2.npy 文件上,如果文件路径末尾没有扩展名 .npy,该扩展名会被自动加上
np.save('outfile2',a)$ cat outfile.npy
?NUMPYv{'descr': '<i8', 'fortran_order': False, 'shape': (5,), }
$ cat outfile2.npy
?NUMPYv{'descr': '<i8', 'fortran_order': False, 'shape': (5,), } 可以看出文件是乱码的,因为它们是 Numpy 专用的二进制格式后的数据。
我们可以使用 load() 函数来读取数据就可以正常显示了:
import numpy as np b = np.load('outfile.npy')
print (b)
np.savez
numpy.savez() 函数将多个数组保存到以 npz 为扩展名的文件中。
numpy.savez(file, *args, **kwds)参数说明:
- file:要保存的文件,扩展名为 .npz,如果文件路径末尾没有扩展名 .npz,该扩展名会被自动加上。
- args: 要保存的数组,可以使用关键字参数为数组起一个名字,非关键字参数传递的数组会自动起名为 arr_0, arr_1, … 。
- kwds: 要保存的数组使用关键字名称。
import numpy as np a = np.array([[1,2,3],[4,5,6]]) b = np.arange(0, 1.0, 0.1) c = np.sin(b) # c 使用了关键字参数 sin_array np.savez("runoob.npz", a, b, sin_array = c) r = np.load("runoob.npz") print(r.files) # 查看各个数组名称 print(r["arr_0"]) # 数组 a print(r["arr_1"]) # 数组 b print(r["sin_array"]) # 数组 c
savetxt()
savetxt() 函数是以简单的文本文件格式存储数据,对应的使用 loadtxt() 函数来获取数据。
np.loadtxt(FILENAME, dtype=int, delimiter=' ')
np.savetxt(FILENAME, a, fmt="%d", delimiter=",")
参数 delimiter 可以指定各种分隔符、针对特定列的转换器函数、需要跳过的行数等。
import numpy as np a = np.array([1,2,3,4,5])
np.savetxt('out.txt',a)
b = np.loadtxt('out.txt') print(b)输出结果为:
[1. 2. 3. 4. 5.]
使用 delimiter 参数:
import numpy as np a=np.arange(0,10,0.5).reshape(4,-1)
np.savetxt("out.txt",a,fmt="%d",delimiter=",") # 改为保存为整数,以逗号分隔
b = np.loadtxt("out.txt",delimiter=",") # load 时也要指定为逗号分隔
print(b) 
7.ndarray形状操作
7.1. 改变 ndarray 数组形状
1.1 reshape()
一维数组有一个轴,长度即它的元素个数。
二维数组有两个轴,第一个轴的长度是行的个数,第二个轴的长度是行的元素个数。
而秩,即轴的数量或者维度的数量
回忆一下之前说过的函数,看看二维数组的秩、轴、或者说维度
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]],np.int32)
print(x)
print(x.ndim) #秩,即轴的数量或维度的数量
print(x.shape) #数组的维度,对于矩阵,n 行 m 列
print(x.size) #数组元素的总个数,相当于 .shape 中 n*m 的值[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
2
(4, 3)
12
可以看出,这个ndarray的形状就是(4,3),即有 4 行数据,每行 3 个数据。
那如果想改变这个ndarray的形状呢,最常用的就是 reshape 函数
y=x.reshape(3,2,2) # reshape不会改变原来ndarray数据的形状,只会返回一个新的
print(y)
print(y.ndim) #秩,即轴的数量或维度的数量
print(y.shape) #数组的维度,对于矩阵,n 行 m 列
print(y.size) #数组元素的总个数,相当于 .shape 中 n*m 的值(3,2,2),即有 3 行,每行有 2 个子数组,每个子数组有2个元素。
运行结果是
[[[ 1 2]
[ 3 4]][[ 5 6]
[ 7 8]][[ 9 10]
[11 12]]]
3
(3, 2, 2)
12
如果在 reshape 操作中将 size 指定为-1,则会自动计算其他的 size 大小:
print("*"*40)
print(x)
x.reshape(4,-1) #成功了返回 None
print(x)运行结果是

1.2 扁平化函数 ravel() 和 flatten()
想将多维数组转化为一维数组,一般有 ravel() 和 flatten(),两者都能实现这个效果
print("*"*40)
print(x)print("*"*40)
print(x.ravel())
print(x)print("*"*40)
print(x.flatten())
print(x)运行结果如下
****************************************
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
****************************************
[ 1 2 3 4 5 6 7 8 9 10 11 12]
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
****************************************
[ 1 2 3 4 5 6 7 8 9 10 11 12]
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
但是ravel() 和 flatten()两者功能相同,在内存上有很大的不同,一般推荐使用 flatten(),为什么呢?
因为flatten()分配了新的内存,返回的是一个真实的数组,而ravel()返回的是一个数组的视图,大家可以用mysql里面的视图去理解,但是又不完全一样,因为ravel() 返回的数组地址和原数组并不一样,有点类似于引用,修改视图的时候可能会影响原本的数组。也可以用深拷贝和浅拷贝来类比。
所以,我非常不推荐使用 ravel(),除非你就是想利用这个特性。
1.3 resize()
reshape() 改变 ndarray 的形状后返回副本,原有数组不会变化,resize() 则会修改数组本身
代码如下
print("*"*40)
print(x)
print(x.resize(2,6)) #成功了返回 None
print(x)运行结果如下
****************************************
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
None
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
1.4 转置函数 transpose()
简单来说,就相当于数学中的转置,在矩阵中,转置就是把行与列相互调换位置;
但是它返回的是一个副本,原有的数组结构没有改变。
print("*"*30)
print(x)
print("*"*30)
print(x.transpose())
print("*"*30)
print(x)******************************
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
******************************
[[ 1 7]
[ 2 8]
[ 3 9]
[ 4 10]
[ 5 11]
[ 6 12]]
******************************
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
7.2. 将不同数组堆叠在一起
- stack():沿着新的轴加入一系列数组。
- vstack():堆栈数组垂直顺序(行)
- hstack():堆栈数组水平顺序(列)。
- dstack():堆栈数组按顺序深入(沿第三维)。
- concatenate():连接沿现有轴的数组序列。
2.1 stack()
按照指定的轴对数组序列进行联结。
语法格式:numpy.stack(arrays, axis=0, out=None)
参数:arrays :数组序列,数组的形状(shape)必须相同;
axis参数指定新轴在结果尺寸中的索引。例如,如果axis=0,它将是第一个维度,如果axis=-1,它将是最后一个维度。不太好理解,大家直接看代码运行结果吧,或者等有需要时候再仔细看。
print("*"*30)
print(x)
z=x
print("*"*30)
print(np.stack((x,z)))
print("*"*30)
print(np.stack((x,z),0))
print("*"*30)
print(np.stack((x,z),1))******************************
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
******************************
[[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]][[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]]
******************************
[[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]][[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]]
******************************
[[[ 1 2 3 4 5 6]
[ 1 2 3 4 5 6]][[ 7 8 9 10 11 12]
[ 7 8 9 10 11 12]]]
2.2 vstack() 和 hstack()
vstack() 沿着第一个轴堆叠数组。
语法格式:numpy.vstack(tup)
参数:tup:ndarrays数组序列,如果是一维数组进行堆叠,则数组长度必须相同;除此之外,其它数组堆叠时,除数组第一个轴的长度可以不同,其它轴长度必须一样。
hstack()沿着第二个轴堆叠数组 语法格式:numpy.hstack(tup)
参数:tup:ndarrays数组序列,除了一维数组的堆叠可以是不同长度外,其它数组堆叠时,除了第二个轴的长度可以不同外,其它轴的长度必须相同。原因在于一维数组进行堆叠是按照第一
个轴进行堆叠的,其他数组堆叠都是按照第二个轴堆叠的。
print("*"*30)
print(x)
z=x
print("*"*30)
print(np.vstack((x,z)))
print("*"*30)
print(np.hstack((x,z)))运行结果如下
******************************
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
******************************
[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]
[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
******************************
[[ 1 2 3 4 5 6 1 2 3 4 5 6]
[ 7 8 9 10 11 12 7 8 9 10 11 12]]
2.3 dstack()
功能:将列表中的数组沿深度方向进行拼接。
当数组为2维数组(M,N)或1维数组(N,)时,首先分别将其维度改变为(M,N,1)、(1,N,1),然后
沿着第三根轴进行拼接。(使用函数dsplit可以将数组沿深度方向进行分隔)。
语法格式:numpy.dstack(tup)
参数:数组组成的列表,其中每个数组的长宽必须保持一致
一维数组的拼接
a = np.array((1,2,3))
b = np.array((4,5,6))
np.dstack((a,b))
二维数组的拼接
a = np.array(((1,2,3),(4,5,6)))
b = np.array(((7,8,9),(10,11,12)))
np.dstack((a,b))
2.4 concatenate()
功能:能够一次完成多个数组的拼接。
语法格式:numpy.concatenate((a1,a2,...), axis=0)
参数:a1,a2,...是数组类型的参数
a = np.array(((1,2,3),(4,5,6)))
b = np.array(((7,8,9),(10,11,12)))
c=np.concatenate((a,b))
print(c) 
7.3. 将一个数组拆分成几个较小的数组
3.1 split()
numpy.split(ary, indices_or_sections, axis=0)功能:把一个数组从左到右按顺序切分
ary:要切分的数组 ,
indices_or_sections:如果是一个整数,就用该数平均切分,如果是
一个数组,为沿轴 切分的位置(左开右闭)
axis:沿着哪个维度进行切向,默认为0,横向切分。为1时,纵向切分
请注意,如果indices_or_sections不能正确的平均切分,则会报错:“ValueError: array split does not result in an equal division ”
print("*"*30)
y=np.array([[[ 1, 2],[ 3 , 4]],[[ 5 , 6],[ 7 , 8]],[[ 9 ,10],[11 ,12]]],np.int32)
print(np.split(y,3,0))print("*"*30)
x = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]],np.int32)
print(np.split(x,3,1))
3.2 vsplit() 和 hsplit()
如果把 hstack() 和 vstack() 两个函数弄明白了,这两个拆分函数就不用多说了。