1、归并排序——归并
- 假设现在的列表分为两段有序,如何将其合成为一个有序列表
- 这种操作称为一次归并
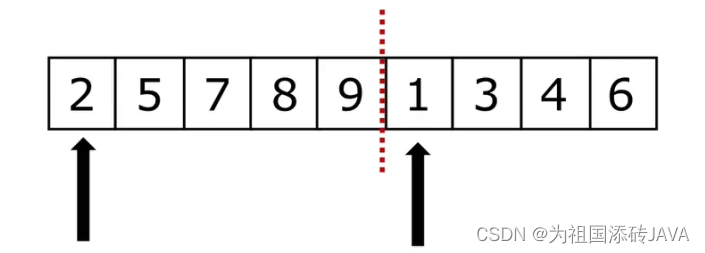
归并过程描述:(前提是两段列表分别有序)
两段有序列表进行对比,1和2进行对比选出最小的数,1出列,然后指针向后移,2和3在进行对比,2出列,指针向后移,指向5,以此类推......
# 归并排序
def merge(li, low, mid, high):''':param li:列表[AB]:param low:A列表的第一个位置:param mid:A列表的最后一个位置,mid+1为B列表的第一个位置:param high:B列表的最后一个位置:return:'''i = lowj = mid + 1ltmp = [] # 临时列表while i <= mid and j <= high: # 只要左右两边都有数if li[i] < li[j]:ltmp.append(li[i])i = i + 1else:ltmp.append(li[j])j = j + 1# 第一部分跳出之后,肯定一部分没数了while i <= mid:ltmp.append(li[i])i += 1while j <= high:ltmp.append(li[j])j += 1li[low:high + 1] = ltmpli = [2, 4, 7, 8, 3, 6, 9, 10]
print(li)
merge(li, 0, 3, 7)
print(li)
2、归并排序——使用归并
- 之前介绍的归并条件是两个列表分别有序,但是在实际中不会遇到这样的特殊情况,因此我们需要进行以下操作
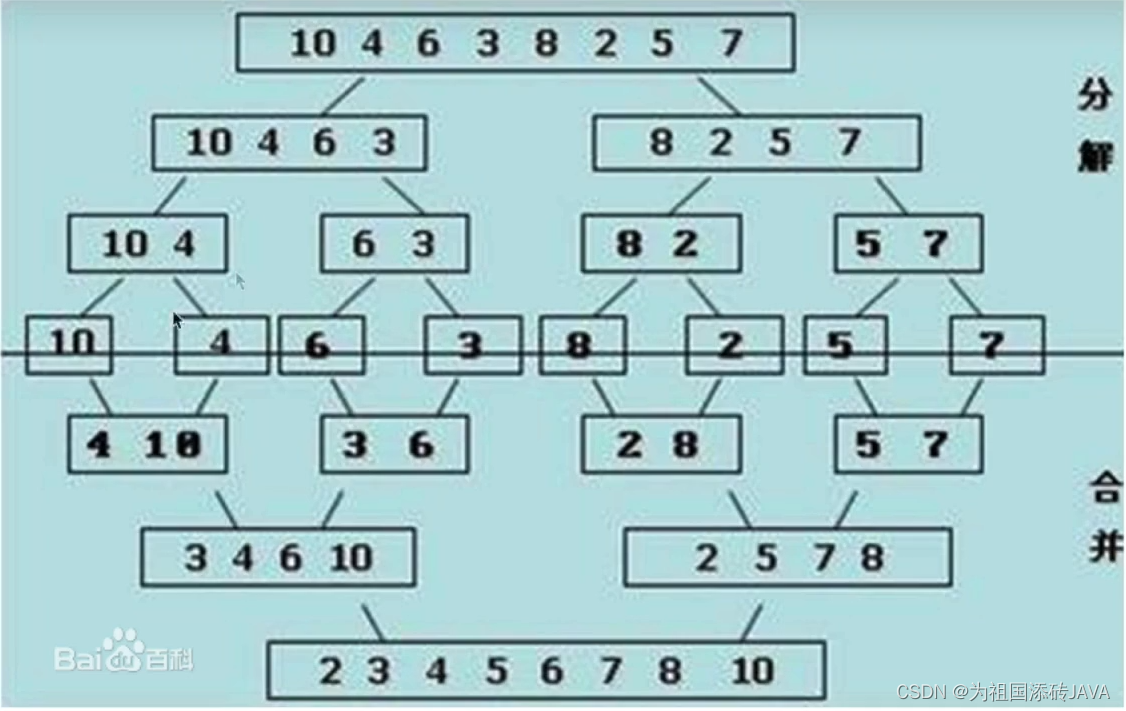
- 分解:将列表越分越小,直至分成一个元素
- 终止条件:一个元素是有序的
- 合并:将两个有序列表归并,列表越来越大
- 过程如下图所示:
# 归并排序
def merge(li, low, mid, high):''':param li:列表[AB]:param low:A列表的第一个位置:param mid:A列表的最后一个位置,mid+1为B列表的第一个位置:param high:B列表的最后一个位置:return:'''i = lowj = mid + 1ltmp = [] # 临时列表while i <= mid and j <= high: # 只要左右两边都有数if li[i] < li[j]:ltmp.append(li[i])i = i + 1else:ltmp.append(li[j])j = j + 1# 第一部分跳出之后,肯定一部分没数了while i <= mid:ltmp.append(li[i])i += 1while j <= high:ltmp.append(li[j])j += 1li[low:high + 1] = ltmpdef merge_sort(li, low, high):'''归并排序'''if low < high: # 至少有两个元素# 使用递归分解mid = (low + high) // 2merge_sort(li, low, mid)merge_sort(li, mid + 1, high)# 使用merge合并merge(li, low, mid, high)# li = [2, 4, 7, 8, 3, 6, 9, 10]
# print(li)
# merge(li, 0, 3, 7)
# print(li)li = list(range(100))
import randomrandom.shuffle(li)
print(li)
merge_sort(li, 0, len(li) - 1)
print(li)
3、归并排序算法的时间复杂度和空间复杂度
- 时间复杂度O(nlogn)
- 空间复杂度O(n)(递归)
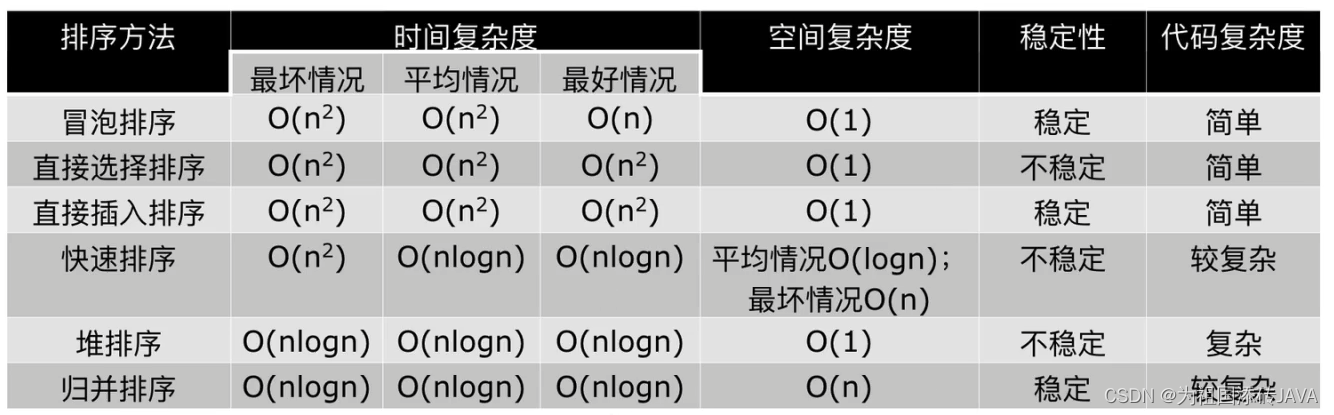
4、基于前两部分的三种排序算法小结
- 三种排序算法的时间复杂度都是O(nlogn)
- 一般情况下,就运行时间而言
- 快速排序<归并排序<堆排序
- 三种排序算法的缺点:
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
5、深拷贝和浅拷贝的区别
- 浅拷贝只复制指向某个对象的指针,而不复制对象本身,新旧对象还是共享同一块内存(分支)
- 深拷贝会另外创造一个一模一样的对象,新对象跟原对象不共享内存,修改新对象不会改到原对象,是“值”而不是“引用”(不是分支)