请点击↑关注、收藏,本博客免费为你获取精彩知识分享!有惊喜哟!!
考点一
截位速算
(一)加法截位
1. 适用题型:当选项与材料的数据精确度不一致,即粗略计算时,可根据选项对数据进行截位,只用算出其中的一位或者几位就可以得出答案。
2. 具体方法:选项首位相同,最大位数保留2位;选项首2位不同,最大位数保留3位。
(二)除法截位
1. 截位直除法先看选项,计算时对分母进行截位计算。
(1) 截两位:选项首位不同,将分母从左向右截两位,第三位四舍五入。
(2) 截三位:选项首位相同,第二位不同,将分母从左向右截三位,第四位四舍五入。
(3) 当选项首二位都相同,或者选项本身很接近时,需要进行精确计算。
注:对于存在小数点的数字同样适用截位直除法。
例1
3024+1067+2433+2151=( )
A. 6千多 B. 7千多 C. 8千多 D. 9千多
解析
选项首位数字不同只要找出第一位数字是几就能得出答案,我们可以从左到右截取2位计算就可以了,所以估算为30+11+24+22结果算出来是8开头。
故正确答案为C。
例2
6874+12039+5493+3347=( )
A. 23353 B. 25353 C. 27753 D. 29353
解析
当选项的第一位相同但是第二位不同时从左往右截取3位,理论上应该得出687+120+550+335,我们发现得不出答案。原因是数量级不同,一个5位数其余都是4位数。这里告诉大家截取最大位数从左往右截取3位,其实意味着从右往左舍去2位,所以其余数也要从右往左舍去2位,正确应该得出69+120+55+33=277。
故正确答案为C。
例3
13863÷2162=( )
A. 4.78 B. 6.41 C. 3.22 D. 5.82
解析
第一步,观察选项,选项的首位不同。第二步,因选项首位不同,所以四舍五入保留前两位,即14÷2≈7,又因为分子四舍五入变大了,所以答案小于7。
故正确答案为B。
例4
793.5/923.8=( )
A. 81% B. 84% C. 86% D. 89%
解析
四个选项均为两位数,在同一数量级,则在计算过程中可以不考虑小数点,根 据截位直除法可知对分母截三位,变为793.5/924,可以直接看成793.5/ 924,首位商 8,第二位接近 6,选 C。
故正确答案为C。
考点二
分数比较
(一)分数性质
1. 分母相同的两个分数,分子大的那个分数比较大。
2. 分子相同的两个分数,分母大的那个分数比较小。
推论:两个分数比较时,分子相对大且分母相对小的分数值较大。
(二)量级比较
1. 分子>分母:8712/177和7912/1712第一个分数商第一位在十位上,第二个商在个位,故8712/177>7912/1712。
2. 分子<分母:1234/23456和2345/12345采取补0法:第一个分数分子需要补两个0,即123400/23456,这样分子才够除,补几个0就意味着商到小数点后几位,很明显第一个分数商到小数点后两位;第二个分数需要补一个0,即23450/12345,那么,只需要商到小数点后一位;则1234/23456<2345/12345。
3. 分子>分子,分母>分母:竖着直接除,或者横着看速度(谁快谁牛气,慢的看成1)。如:5/6和7/8,横着看5到7和6到8的变化速度,5到7的变化速度为(7-5)/5=2/5,6到8的变化速度为(8-6)/6=2/6,显然分子变化速率快,则将5/6和7/8看成5/1和7/1,易知5/6<7/8。
(三)化同法
化同法:两个分数的分子/分母有明显的倍数关系,那么就可以将分子/分母化同后再比较。
比如:122/377和246/797。122*2.02/377*2.02=246/750+ , 明显前者大于后者。
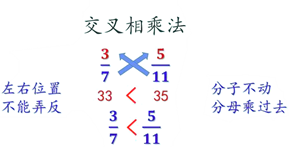
(四)交叉相乘法
交叉相乘法:分子不动,分母交叉相乘移过去。比较乘积大小即分数大小。
(五)差分法
差分法:当两个分数分子分母比较接近时,可以考虑使用差分法。定义分子与分母都比较大的分数叫“大分数”,分子与分母都比较小的分数叫“小分数”,而这两个分数的分子、分母分别做差得到的新的分数我们定义为“差分数”。例如:324/53.1与313/51.7比较大小,其中324/53.1就是“大分数”,313/51.7就是“小分数”,而324-313/53.1-51.7=11/1.4就是“差分数”。 因为11/1.4>313/51.7(可以通过“直除法”或者“化同法”简单得到),所以324/53.1>313/51.7。
“差分法”使用基本准则—— “差分数”代替“大分数”与“小分数”作比较:
① 若差分数比小分数大,则大分数比小分数大;
② 若差分数比小分数小,则大分数比小分数小;
③ 若差分数与小分数相等,则大分数与小分数相等。
(六)直除法
直除法:可以通过估算首位或首二位来比较分数大小。(详见“资料分析之截位直除”篇)
考点三
基期与现期
(一)基本概念
1. 基期是一个时间的概念,指的是基础期、起始期,即起始时间。基期量指的是起始时间的数量,一般作为参照基数,其它时间段的数据都参照这个基数,计算增长率等。
2. 现期相对于基期而言,指的是其它时间段。现期量即其它时间段的数量,与基期进行比较的时期的数值。
3. 增长量:现期量相对于基期量增长多少,指具体增加的情况,有数字,有单位。增长率:现期量相对于基期量增长百分之多少,无单位。
如 2019 年(现期)我的体重 120 斤,2018年(基期)我的体重 100 斤。则增长量为120-100=20斤,增长率为(120-100)/100=20%。
(二)题型识别
给现在,求以前某时期的值。问的时间与材料时间不一致,问的是材料时间之前的就是求基期。如给出时间 2019年,只要问时间轴左侧,如2016年、2017年,就是求基期。
(三)计算公式
1. 基期量=现期量-增长量
2. 基期量=现期量/(1+r)(r为增长率)
3. 现期=基期×(1+r)
(四)速算技巧
1. 加减计算
只要选项精度和材料一致,且选项尾数各不相同,可以考虑尾数法。
2. 除法
① |r|>5%,截位直除。
② |r|≤5%,化除为乘。
|r|≤5%时,化除为乘方法(A为现期量):
A/(1+r)≈A - A×r
A /(1-r)≈A + A×r
实例1
2017 年末,全国医疗卫生机构床位 794.0 万张,其中:医院 612.0 万张(占77.1%),基层医疗卫生机构 152.9 万张(占 19.3%)。医院中,公立医院床位占75.7 %,民营医院床位占 24.3%,与上年比较,床位增加 53.0 万张,其中:医院床位增加 43.1 万张,基层医疗卫生机构床位增加 8.7 万张。每千人口医疗卫生机构床位数由 2016 年 5.37 张增加到 2017 年 5.72 张。
2016 年末,全国基层医疗卫生机构拥有床位数量为多少万张?( )
A. 714 B. 568.9 C. 152.9 D. 144.2
解析
材料时间 2017 年,问 2016 年,是问时间轴左侧的时间,即求基期。求“全国基层医疗卫生机构拥有床位数量”,材料中给出了现期量和增长量,简单加减计算,基期量=现期-增长量=152.9-8.7,结合尾数法,尾数为 2, 对应D 项。
故正确答案为D。
实例2
2017 年末,全国民用汽车保有量 21743 万辆,比上年末增长 11.8%。其中私人汽车保有量 18695 万辆,增长 12.9%;民用轿车保有量 12185 万辆,增长 12.0%,其中私人轿车保有量 11416 万辆,增长 12.5%;全国新能源汽车保有量 153.0 万辆,其中新能源汽车新注册登记 65.0 万辆,比上年增加 15.6 万辆。
2016 年末全国私人轿车保有量为( )辆。
A. 10148 B. 11006 C. 13879 D. 16559
解析
材料时间 2017 年末,求的是时间轴左侧的 2016 年,求的是基期。问“私人轿车保有量”,材料中给出了现期和增长率,基期=现期/(1+r)=1141/(1+12.5%),观察选项差距,A、B 项首位相同,次位差 1-1=首位 1,选项差距小,分母截三位计算,11416/113,首位商 1,次位商 0,第三位商 3,对应A 项。
故正确答案为A。
实例3
2016 年,某市全年规模以上计算机、通信和其他电子设备制造业实现利润 84.8 亿元,增长 36.8%;专用设备制造业实现利润 73.9 亿元,增长 70.3%。2015 年该市规模以上专用设备制造业约实现利润多少亿元?( )
A. 22 B. 33 C. 43 D. 55
解析
题中,2015年该市规模以上专用设备制造业利润为基期,2016年该市规模以上专用设备制造业利润为现期。已知现期为73.9亿元,增长率为70.3%,求基期。基期量=现期量/(1+r)=73.9/(1+70.3%),从选项来看,各选项之间的差距较大,那么式子列出后,首选估算法,尽量将数据往整数上靠近,分子73.9可看做74,分母1.703可以直接看做1.7;于是转化为74÷17≈4.35,接近选项C。
故正确答案为C。
考点四
增长量与增长率
(一)增长量概述
1. 常考题型
① 增长量的计算
② 增长量的比较
2. 基本公式
① 增长量=现期量-基期量
(在加减法中可以使用尾数法和截位法进行速算)
② 增长量=基期量×增长率
(在乘法中可以用放缩法或者特殊分数进行计算)
③ 增长量=现期量/(1+增长率)×增长率=A/(1+r)×r
(常考,可以使用特殊分数法计算,即当r=1/n时,增长量=A/(n+1);若r为一个负数,则减少量=A/(n-1)。比较题型时,特殊地,现期量和增长率均大,则增长量大)
原理:

特殊分数(熟记!!):

(二)普通增长率概述
1. 常考题型
① 增长率的计算
② 增长率的比较
注:增长率有正负,正值意为着增加/提高,负值意味着减少/降低。
2. 基本公式
① 增长率r=增长率/基期量=增长量/(现期-增长量)
② 增长率r=(现期-基期)/基期=现期/基期-1
增长率比较题型:
① 当“现期/基期=1+”,用“(现期-基期)/基期”比较。
② 当 “现期/基期=2+”,用“现期/基期”比较。
实例1
2016年,兵团拥有商贸流通企业3357家,比2012年增长77.2%。分行业看,批发零售企业3244家,比2012年增长81.1%;住宿餐饮企业113家,比2012年增长8.7%。
2016年兵团批发零售企业的数量比2012年多出( )家
A. 1391 B. 1453 C. 1518 D. 1604
解析
时间给的是2016年。商贸流通企业的数量给了,分行业看,批发零售企业,住宿餐饮企业的数据也给了,问题问2016年兵团批发零售企业的数量比2012年多出多少家,比2012年多多少家,多后面加一个具体的单位,我们就可以判断这是一道求增长量的题型。我们可以把2016年批发零售企业的数量看作现期,2012年批发零售企业的数量看作基期。定位到材料中,材料已经给了2016年批发零售企业的数量和增长率,所以相当于给了现期量和增长率。所以可以使用增长量的公式,增长量=现期量/(1+增长率)×增长率=A/(1+r)×r。使用特殊分数法进行速算,81.1%近似于80%,而1/8=12.5%,稍微变形一下,可以得到8%=1/12.5,则80%=1/1.25。所以n=1.25,所以使用n+1法则, 增长量= A/(n+1)=3244÷2.25,直除首两位14,看选项B选项最为接近。
故正确答案为B。
实例2
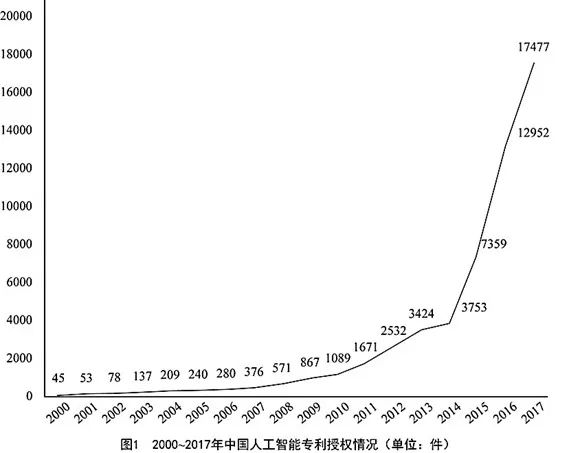
下列年份中,中国人工智能专利授权量增速最快的是( )
A. 2007年 B. 2012年 C. 2015年 D. 2017年
解析
本题考查增长率比较问题。根据材料给的是数据资料,结合增长率计算公式r= (现期-基期)/基期=现期/基期-1,因为本题中15年跟14年的量差距较大,接近2倍关系,所以本题选用第二个公式,比较现期/基期的大小,代入数据可得:2007年为376,2012年为2532,2015年为7359,2017年为17477,其中2015年/2014年=7359/3753的结果非常接近于2,其余年份均比1稍大,则2015年增速最快。
故正确答案为C。
考点五
其他增长率
(一)间隔增长率
1. 基本概念
间隔增长率,也叫隔期增长率,就是已知第二期、第三期的增长率,求第三期对第一期增长百分之多少。
2. 计算公式:
间隔增长率R= r1+ r2+ r1×r2(和+积)
举例示意

如上图,已知2015年相对于为2014年的增长率为r1,2016年相对于2015年的增长率为r2,则2016年相对于2014年的增长率即为间隔增长率,且间隔R= r1+ r2+ r1×r2
3. 计算方法
① 若r1、r2绝对值均小于10%,此时可将公式中的r1×r2项忽略
② r1、r2不能忽略时,一个不变,另一个百化分(乘积保留一位有效数字即可)
如:

③ 取整计算(除同乘异)
如:
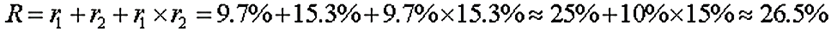
4. 间隔基期
间隔基期=现期/(1+间隔增长率R)
(二)年均增长率
1. 题型识别
如果题目给定一个时间范围要求年均增长率,这就是年均增长率的计算问题。常见的设问方式有:
① XXXX~XXXX年,……的年均增长率/平均增长率约为……
② “X五”期间……的年均增长率/平均增长率约为……
③ XXXX~XXXX年这N年,……年均增长率/平均增长率约为……
2. 基本公式
(1+r)n=现期/基期(n为现期和基期的年份差)
年均增长类问题年份差的判断:
一般情况
如:2011年-2015年:年份差为4;基期:2011年;现期:2015年。
如:2011年-2015年:年份差为5(基期往前推一年);基期:2010年;现期:2015年。
五年规划(全国都一样)
如:十四五期间:年份差为5(基期往前推一年)
基期:2020年;现期:2025年
3. 计算方法
① 直接比较法
当比较年均增长率时,n相同,直接比较“现期/基期”。
② 代入排除法

特殊值记忆:

(三)混合增长率
1. 题型识别
部分与总体之间的增长率关系(整体=部分1+部分2)。
如:
房产、地产、房地产;
出口、进口、进出口;
城镇、农村、全国;
上半年、下半年、全年
2. 核心公式——十字交叉法

3. 判断口诀
① 混合后居中(大于小的,小于大的)
② 偏向基数较大的(基数指的基期量,做题中一般用现期量近似代替)
③ 精算:距离和量成反比(增速差与基数成反比)
实例1
2015年全行业全年生产手表10.7亿只,同比增长3.9%,完成产值约417亿元,同比增长4.3%,增速提高1.9个百分点;生产时钟(含钟心)5.2亿只,同比下降3.7%,完成产值162亿元,同比下降4.7%,降幅扩大1.3个百分点;钟表零配件、定时器及其他计时仪器产值96亿元,同比增长14.3%,增速基本保持上年水平。
2015年我国钟表全行业生产时钟(含钟心)的产值与2013年相比约( )
A. 上升了11% B. 下降了11% C. 上升了8% D. 下降了8%
解析
第一步,本题考查增长率,属于间隔增长率。
第二步,2015年相对于2013年增长百分之多少?定位第二行,2015年生产时钟(含钟心)的产值同比下降4.7%,降幅扩大1.3个百分点。第三步,2015年同比增长率r1=-4.7%(注意:降幅时增长率为负!),2014年同比增长率r2=-4.7%+1.3%=-3.4%。即与2013年相比,2015年的间隔增长率R= r1+ r2+ r1×r2=-4.7%-3.4%+(-4.7%)×(-3.4%)≈-8.1%+5%×3%≈-8%
故正确答案为D。
实例2
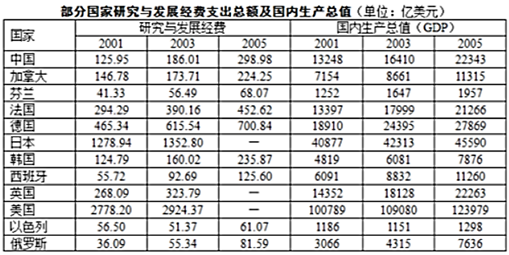
2001~2005年,西班牙研究与发展经费的平均增长率为( )
A. 22.5% B. 50.1% C. 122.5% D. 150.1%
解析

实例3
2020年上半年,我国农产品进出口总额达1159.0亿美元。农产品进口额为807.5亿美元,同比增长13.2%。受新冠肺炎疫情影响,我国农产品出口额同比下降3.8%,为351.5亿美元。
2020年上半年,我国农产品进出口额同比增长约( )
A. 2.5% B. 5.0% C. 7.5% D. 10.0%
解析
根据题目发现求的是增长率,但是我们在材料中发现农产品进出口额只给了个现期量,没有其他量了,无法用基础公式,但是根据进出口=进口+出口,可知求的是混合增长率。口诀“混合增长率居于部分增长率之间,偏向基期量大的一边”可知-3.8%<混合的增长率<13.2%,偏向基期量大的一边,看现期量,是进口的大,偏向进口的增长率,也就是在他们中间的增长率和进口额的增长率之间,即4.7%<混合的增长率<13.2%,排除A选项;还有三个选项无法排除,这时候就需要利用十字交叉法了。
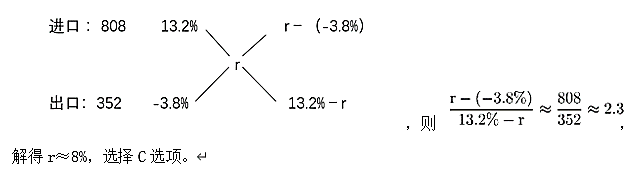
考点六
比重问题
(一)现期比重
1. 题目特征
题干中出现“占……比重”,时间与材料所给时间一致。
2. 基本公式
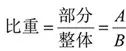
3. 计算方法
找部分、整体及占比三量中的已知量,利用公式结合选项直接求解。
(二)基期比重
1. 题目特征
已知部分的现期量和增长率,以及整体的现期量和增长率,求基期比重。
2. 基本公式
基期比重=

A:部分的现期量
B:总体的现期量
a:部分的增长率
b:总体的增长率
3. 计算方法
① 先截位直除A/B
② 再看(1+b)/(1+a)与1的关系(>,<,=),结合选项选答案
(三)两期比重比较——升降
1. 题目特征
题干中出现“占……比重”以及两个时间。比如2019年A占B的比重与2018年相比上升还是下降。
2. 基本公式

A:现期部分值
B:现期整体值
a:现期部分增长率
b:现期整体增长率
3. 计算方法
① 判方向:题干如果只是让我们判断比重上升还是下降,那就找部分量及整体量增长率,直接比大小即可,其中增长率比较大小时需要带上正负号进行比较。
a>b,部分增长率 > 整体增长率,比重上升。
a<b,部分增长率 < 整体增长率,比重下降。
a=b,部分增长率=整体增长率,比重不变。
② 定大小:若题干中不仅需要判断比重的升降,还进一步问具体变化了几个百分点,大胆选小于|a-b|绝对值的选项。若选项有多个在这个范围之内,则需要进一步计算。
实例1
2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的16.0%;人口总数约为32.1亿人,占全球总人口的43.4%;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的21.7%。
2016年全球贸易总额约为多少万亿美元( )
A. 28 B. 40 C. 33 D. 75
解析
问2016年全球贸易总额,材料给出“….占全球贸易总额的21.7%”,本题为现期比重。已知对外贸易总额约为71885.6亿美元,占全球贸易总额的21.7%”,则2016年全球贸易总额=对外贸易总额÷21.7%=71885÷21.7%=33万亿美元。
故正确答案为B。
实例2
2017年上半年,全国居民人均可支配收入12932元,比上年同期名义增长8.8%; 按收入来源分,全国居民人均工资性收入7435元,增长8.6%,占全国居民人均可支配收入的比重为57.5%。
2016年上半年,全国居民人均工资性收入占全国居民人均可支配收入的比重约为( )
A. 53.6% B. 57.6% C. 60.6% D. 63.6%
解析
第一步本题考查基期比重。


实例3
2017年,全省全年完成快递业务量100.51亿件,同比增长31.0%。其中,同城快递业务量增长29.3%,异地快递业务量增长33.0%,国际和港澳台地区快递业务量增长33.1%。
2017年A省快递业务中,业务量占总业务量比重高于上年水平的分类是( )
A. 仅国际和港澳台地区快递
B. 异地快递、国际和港澳台地区快递
C. 仅同城快递
D. 同城快递、异地快递
解析
问…占…比重高于上年水平的分类,判断本题为两期比重比较。已知2017年,全省全年完成快递业务量同比增长31.0%。若业务量的增长率(a)大于总业务量的增长率(b),即大于31.0%,满足比重高于上年。观察可得异地快递业务量(a=33.0%)和国际和港澳台地区快递业务量(a=33.1%)满足。
故正确答案为B。
实例4
2016 年J省规模以上工业取水量为86.4亿立方米,比上年增长4.4% 。其中直接采自江、河、淡水湖、水库等的地表淡水 68.1 亿立方米 ,比上年增长 3.8% 所占比重比上年下降 0.4 个百分点;自来水取水量15.9 亿立方米,同比增长6.0% 。
J省2016年规模以上工业自来水取水量占总取水量的比重比上年( )
A. 提高 0.3 个百分点 B. 下降 0.3 个百分点
C. 提高 4 个百分点 D. 下降 4 个百分点
解析
本题为两期比重差值计算问题。
2016年J省规模以上工业取水量为86.4亿立方米,增长率为4.4%;自来水取水量15.9亿立方米,增长率为6.0%。由两期比重结论可知:由于6%>4%,故比重应为提高,排除B、D;两期比重差值=
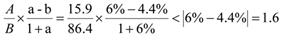
个百分点,只有A选项满足。
故正确答案为A。
考点七
平均数问题
(一)现期平均数
1. 题目特征
问题时间与材料所给时间一致+平均(均/每/单位)。
2. 基本公式
现期平均数=现期总量(A)÷现期个数(B)
3. 计算方法
截位直除。
(二)基期平均数
1. 题目特征
求上一年的平均数。
2. 基本公式

A:现期总量; a:现期总量增长率
B:现期个数; b:现期个数增长率
3. 计算方法
① 先截位直除A/B
② 再看(1+b)/(1+a)与1的关系(>,<,=),结合选项选答案
注:基期平均数与基期比重的计算公式一样,但含义不一样,注意区分体会!
(三)两期平均比较——升降
1. 题目特征
题干中涉及两个时间+平均数问法。
2. 基本公式

3. 判断升降方向
现期总数增长率大于现期个数增长率,平均增长量上升;
a > b,平均数增量上升。
a < b,平均数增量下降。
a=b,平均数增量不变。
注:两期平均数升降比较与两期比重升降比较的计算公式一样,但含义不一样,注意区分体会!
(四)两期平均比较——增长率
1. 题目特征
两个时间+平均+上升/下降+百分之几。
2. 基本公式

实例1—平均数问题
2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,.....2018年前三季度,S省社会物流总费用2682.1亿元,同比增长6.3%。
2018年前三季度,平均每万元社会物流总额产生的物流费用比上年同期( )
A. 下降了不到1% B. 下降了1%以上
C. 上升了不到1% D. 上升了1%以上
解析
根据平均数增长率计算公式,物流费用的增长率为a,物流额的增长率为b,代入数据可得(6.3%-6.4%)/(1+6.4%),下降了不到0.1%,观察选项,仅A选项符合。
故正确答案为A。
由于平均数是一种具体数量,通常有数据亦有量词(单位),所以定量比较两期平均数的时候,我们通常关心现基期平均数的相对差异,也就是说平均数变化的公式计算的是平均数的增长率,一般用

来表示。。
实例2—比重问题
2020年1—2月,我国境内投资者共对全球147个国家和地区的1733家境外企业进行了非金融类直接投资,累计实现投资1078.6亿元人民币,同比增长1.8%。......2020年1—2月,对外投资主要流向租赁和商务服务业、批发和零售业、制造业和采矿业等传统投资领域,占对境外企业非金融类直接投资的比重分别为40.8%、15.1%、11.3%和8.9%。其中流向租赁和商务服务业的投资额同比增长43.2%,成为增速最高的领域。
2020年1—2月,租赁和商务服务业对外投资额占对境外企业非金融类直接投资额的比重比上年同期约( )
A. 上升了3个百分点 B. 上升了12个百分点
C. 下降了3个百分点 D. 下降了12个百分点
解析
将数据代入两期比重差公式
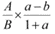
,其中a=43.2%,b=1.8%,即a>b;|a-b|>12%,大胆选择B项上升了12个百分点。
故正确答案为B。
由于比重本身表示一种相对关系,通常用百分数表示,所以定量比较两期比重的时候,我们通常关心现基期比重的绝对差异,也就是说比重变化的公式计算的是比重的差值,或者说比重的增长量。
考点八
倍数问题
(一)倍数问题的基本考法与技巧
资料分析题在统计数据的时候,往往涉及多个统计主体以及多个统计时间,那么不同主体可以求解倍数关系,不同时间可以求解倍数关系。常见的特征是“某年A是B的几倍”。那么命题人在设置这些问题的时候,常见的考法有下述三种:
① 2021年浙江行测真题问法为“2015年S省规模以上工业企业所有者权益约是限额以上批发和零售业企业的几倍?”直接求解A是B的几倍,简单除法计算即可。
公式:现期倍数=A/B
② 2014年天津真题问法为“2004年移动电话用户总量是固定电话用户总量的几倍”材料中的时间是2005年,因此本题求解的基期倍数。将基期和倍数两个考点进行了杂糅。
公式:基期倍数=
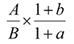
(先截位直除A/B,再看(1+b)/(1+a)与1的关系)
③ 2009年江西真题“2009年第一季度,违反产品质量法规案件的减少量是违反商标法规案件减少量的几倍”,这种问法考生要注意主语,是减少量,负的增长量;因此本题也就是求解增长量的倍数。
(二)倍数问题的易错点
在倍数问题的考查中有一个经典的易错点,就是问题“A是B的几倍”与“A比B多几倍”的区别,前者是简单的倍数求解,后者求解的是增长倍数,实际上就是增长率的求解。因此前者和后者在答案上有个相差一倍的结果。
(三)倍数问题的难点
倍数问题的考查有一个难点就是对于隔年倍数的考查,这种题目的设计往往就是给了现期量和两个时期的增长率,让我们求解隔年倍数。
公式:间隔倍数=间隔增长率+1
回顾:间隔增长率R= r1+ r2+ r1×r2(和+积)
实例1
2014年我国经济在转型升级中步入中高速发展的“新常态”,战略性新兴产业和生产性服务业逆势上行,渐成拉动经济增长的两大“新引擎”。
以发展速度论,新业态快速进入百姓生活,新型服务业攻城略地,势如破竹。2014年,金融业增加值增速较快,比第三产业增加值增速8.1%快2.1个百分点。电子商务全国网上零售增长赢得最佳绩,比全社会消费品零售总额增速12.0%快37.7个百分点,并拉动快递业务量较上年增长61.6%之后再创51.9%的高增速。
2014年我国的快递业务量约是2012年的多少倍?( )
A. 1.8倍 B. 2.1倍 C. 2.5倍 D. 3.3倍
解析
题干中2014年和2012年之间间隔了2013年,且求解得是两年之间的倍数关系,属于间隔倍数题目。题目中已知:2014年快递业务量较上年增长61.6%之后再创51.9%的高增速。可知:间隔增长率R=61.6%+51.9%+61.6%×51.9%≈1.45,间隔倍数=1+1.45=2.45倍。
故正确答案为C。
实例2
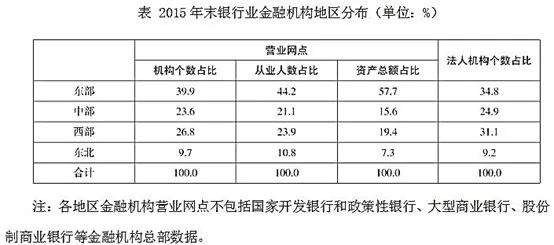
问题:2015年末,我国东部地区的银行业金融机构从业人数比东北地区的多( )倍
A. 1 B. 2 C. 3 D. 4
解析

故正确答案为C。