#数据结构
基础知识
数据结构:相互之间存在的一种多种的特定关系的数据元素的集合
逻辑结构:
线性表:最基本最简单的一种数据结构,一对一逻辑关系。
集合结构、线性结构、树形结构、图形结构
物理结构:顺序存储、链式存储
逻辑结构是面向问题的,物理结构是面向计算机的。物理结构的基本目标就是将数据结构及其逻辑关系存储到计算机内存中去。
什么是树?
前端中的树:dom tree+css rule = render tree,渲染和重绘
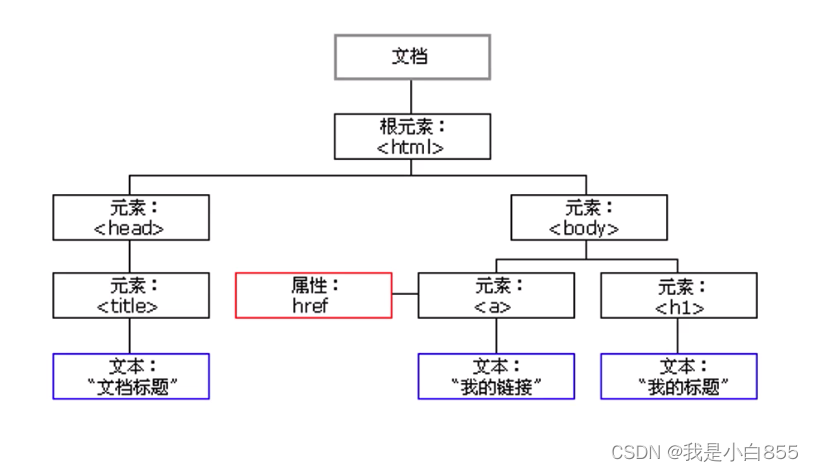
计算机中的树:
在windows系统中,一切东西都是存储在硬盘上,windows是通过某个硬盘-某个硬盘的分区-分区上特定的系统文件
linux系统中一切都是存在唯一的一个虚拟文件系统,这个虚拟的文件系统时树状的一个结构,一切都以根/目录开始
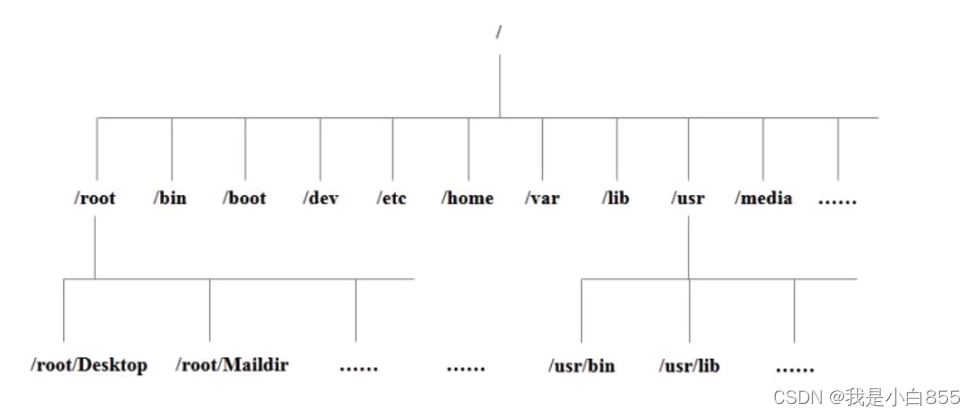
每种数据结构都有自己特定的应用场景。
数组:
- 查询(通过下标查询会很快)
- 插入和删除数据的时候,效率会很低,需要有大量的位移
链表:
- 插入和删除效率很高,
- 查找效率很低,需要从头开始依次访问链表中每个数据项,直到找到
哈希表:
- 插入、删除、查询效率都是很高,
- 空间利用率不高,底层使用的是数组,某些是单元没有被利用的
- 哈希表中的元素是无序的,不能够按照特定的顺序来便来哈希表中的元素,不能够快这的找出哈希表中的最大值或者最小值
树的概念
树:树(Tree)是n( n >= 0 )个结点的有限集,n=0,称为空树。
从逻辑上看,树具有如下特点:
- 任何非空树有且仅有一个结点没有前驱结点,这个结点就是根结点
- 除根节点外,其余的结点有且仅有一个直接的前驱结点
- 包括根节点在内,每个结点可以有多个后继结点
- 树形结构是一种具有递归特性的数据结构(任何一棵子树又满足树的概念)
- 树形结构的数据元素之间存在的关系的是:一对多,或者是多对一的关系
树的术语

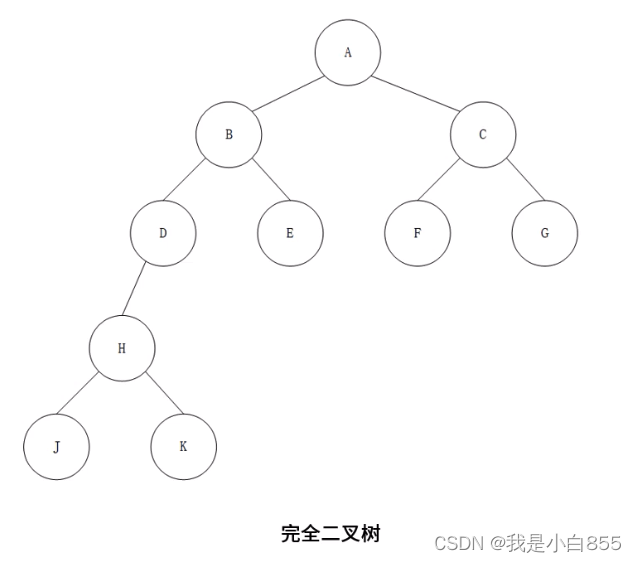
- 结点的度:结点所拥有的子树的个数
- 树的度:树中结点度的最大值,树的度为3
- 叶子 (终端结点) : 度为0的结点。K结点、L结点、F结点,都是叶子结点
- 分支结点(非终端结点):度不为0的结点。除根结点之外的分支结点统称为:内部结点。根结点我们又称为:开始结点
- 子结点: 节点所拥有子树的根节点称为该节点的子节点。 (结点的直接后继,结点的子树的根)
- 父结点: 如果节点拥有子节点,则该节点为子节点的父节点。(结点的直接前驱)
- 兄弟结点: 与节点拥有相同父节点的节点
- 子孙结点:节点向下路径上可达的节点
- 祖先结点:从根结点到该结点所经历分支上的所有结点
- 路径: 从节点到子孙节点过程中的边和节点所组成的序列(这个结点"自上而下的通过每条路径上的每条边)
- 结点的层: 根节点的层: 1,其余结点的层数等于父结点的层数加1,有些教科书: 假设根节点是0
- 树的深度(高度) : 树中所有结点层数的最大值
- 有序树:如果将树中结点的各子树看成从左至右是有次序的,不能互换的
- 无序树:不是有序树
树的存储结构
计算机只能是顺序或者是链式的存储,所以树这样的结构是不能够直接存储的,要将其转换为顺序或者是链式存储。
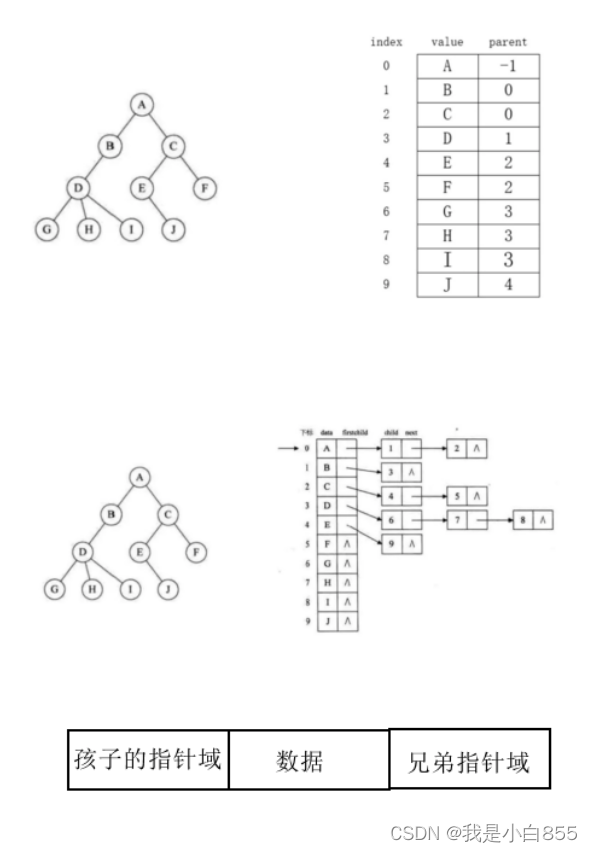
- 双亲表示法:双亲表示法采用数组存储普通的树,其核心思想:顺序存储每个结点的同时,给各个结点附加一个记录其父结点位置的变量,存储的父结点的下标。实际操作的时候,就是从上往下,顺序去遍历一棵树,并为相应的域赋值。优点:可以快速的获取任意结点的父结点位置。缺点:如果要获取某个结点的子结点需要遍历。
- 孩子表示法:孩子表示法是建立多个指针域,指向它的子结点的地址。也就是说,任何一个结点,都掌据它所有子结点的信息。数组+链表的来实现。顺序表=>数组,从树的根结点开始,使用数组依次存储树的各个结点,需要注意的是:孩子表示法会给各个结点配备一个链表,用于存储各结点的孩子结点位于数组中的位置,如果说,结点没有子结点(叶子结点) ,则该结点的链表为空链表
- 孩子兄弟表示法:把普通的树,转成二叉树:从树的根结点开始,依次用链表存储各个结点的孩子结点和兄弟结点二叉树:其实所有的树的本质都是可以使用二叉树进行模拟出来的,所以二叉树非常重要
二叉树
如果说树每个结点最多只能有两个子结点,这样树我们称为: 二叉树。
只有两个分叉的树二叉树是n个结点(n>=0) 个结点的有限集合。
如果这个集合是空集叫空二叉树。
特点:
每个结点最多有两棵子树,=>二叉树种不存在度大于2的结点
左子树和右子树是有序的,次序不能任意颠倒的
即使树中某个结点只有一棵子树,也要区分它是左子树还是右子树
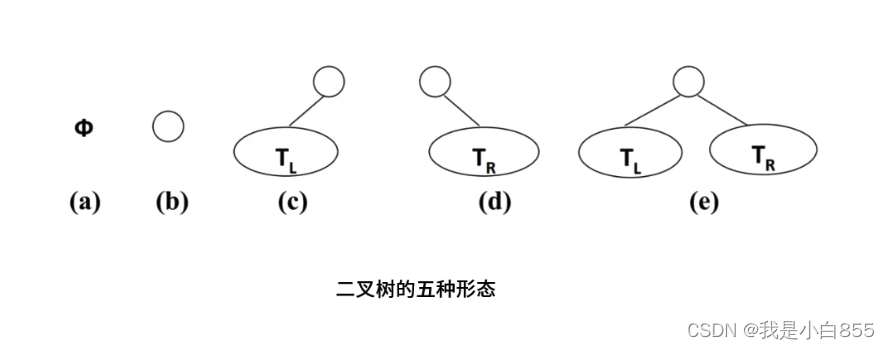
满二叉树:在一棵二叉树中,如果所有的分支结点都存在左子树和右子树,并且所有的叶子都在同一层上,这样的又树就是满二叉树
满二又树叶子只能出现在最下一层,出现在其他层,不可能达成平衡,非叶子结点的度一定是2。