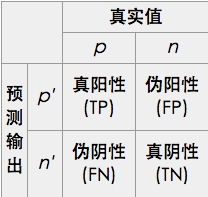
原理：

既能做分类，又能做回归。
分类：基尼值作为节点分类依据。
回归：最小方差作为节点的依据。

节点越不纯，基尼值越大，熵值越大
方差越小越好。
总体的基尼值：0.343
## 代码实践

#整个c4.5决策树的所有算法：
import numpy as np
import operatordef creatDataSet():"""outlook-> 0:sunny | 1:overcast | 2:raintemperature-> 0:hot | 1:mild | 2:coolhumidity-> 0:high | 1:normalwindy-> 0:false | 1:true"""dataSet = np.array([[0, 0, 0, 0, 'N'],[0, 0, 0, 1, 'N'],[1, 0, 0, 0, 'Y'],[2, 1, 0, 0, 'Y'],[2, 2, 1, 0, 'Y'],[2, 2, 1, 1, 'N'],[1, 2, 1, 1, 'Y']])labels = np.array(['outlook', 'temperature', 'humidity', 'windy'])return dataSet, labelsdef createTestSet():"""outlook-> 0:sunny | 1:overcast | 2:raintemperature-> 0:hot | 1:mild | 2:coolhumidity-> 0:high | 1:normalwindy-> 0:false | 1:true"""testSet = np.array([[0, 1, 0, 0],[0, 2, 1, 0],[2, 1, 1, 0],[0, 1, 1, 1],[1, 1, 0, 1],[1, 0, 1, 0],[2, 1, 0, 1]])return testSetdef dataset_entropy(dataset):"""计算数据集的信息熵"""classLabel=dataset[:,-1]labelCount={}for i in range(classLabel.size):label=classLabel[i]labelCount[label]=labelCount.get(label,0)+1     #将所有的类别都计算出来了#熵值(第一步)cnt=0for k,v in labelCount.items():cnt += -v/classLabel.size*np.log2(v/classLabel.size)return cnt#接下来切分,然后算最优属性
def splitDataSet(dataset,featureIndex,value):subdataset=[]#迭代所有的样本for example in dataset:if example[featureIndex]==value:subdataset.append(example)return np.delete(subdataset,featureIndex,axis=1)def classLabelPi(dataset):#多叉树classLabel=dataset[:,-1]labelCount={}for i in range(classLabel.size):label=classLabel[i]labelCount[label]=labelCount.get(label,0)+1valueList=list(labelCount.values())sum=np.sum(valueList)pi=0for i in valueList:pi+=(i/sum)**2return pidef chooseBestFeature(dataset,labels):"""选择最优特征，但是特征是不包括名称的。如何选择最优特征：增益率最小"""#特征的个数featureNum=labels.sizebaseEntropy=dataset_entropy(dataset)#设置最大增益值maxRatio,bestFeatureIndex=0,None#样本总数n=dataset.shape[0] #最小基尼值 minGini=1for i in range(featureNum):#指定特征的条件熵featureEntropy=0gini=0#返回所有子集featureList=dataset[:,i]featureValues=set(featureList)for value in featureValues:subDataSet=splitDataSet(dataset,i,value) pi=subDataSet.shape[0]/n gini+=pi*(1-classLabelPi(subDataSet))  if minGini > gini:minGini=ginibestFeatureIndex=ireturn bestFeatureIndex #最佳增益def mayorClass(classList):labelCount={}for i in range(classList.size):label=classList[i]labelCount[label]=labelCount.get(label,0)+1sortedLabel=sorted(labelCount.items(),key=operator.itemgetter(1),reverse=True)return sortedLabel[0][0]def createTree(dataset,labels):"""参考hunt算法那张图片"""classList=dataset[:,-1]if len(set(dataset[:,-1]))==1:return dataset[:,-1][0] #返回类别if labels.size==0 or len(dataset[0])==1:  #条件熵最少的一定是类别最多的#条件熵算不下去的时候，return mayorClass(classList)bestFeatureIndex=chooseBestFeature(dataset,labels)bestFeature=labels[bestFeatureIndex]dtree={bestFeature:{}}  #用代码表示这棵树featureList=dataset[:,bestFeatureIndex]featureValues=set(featureList)for value in featureValues:subdataset=splitDataSet(dataset,bestFeatureIndex,value)sublabels=np.delete(labels,bestFeatureIndex)dtree[bestFeature][value]=createTree(subdataset,sublabels) #将原始的labels干掉一列return dtreedef predict(tree,labels,testData):#分类，预测rootName=list(tree.keys())[0]rootValue=tree[rootName]featureIndex =list(labels).index(rootName)classLabel=None for key in rootValue.keys():if testData[featureIndex]==int(key):if type(rootValue[key]).__name__=="dict":classLabel=predict(rootValue[key],labels,testData)    #递归else:classLabel=rootValue[key]return classLabeldef predictAll(tree,labels,testSet):classLabels=[]for i in testSet:classLabels.append(predict(tree,labels,i))return classLabelsif __name__ == "__main__":dataset,labels=creatDataSet()# print(dataset_entropy(dataset)# s=splitDataSet(dataset,0)# for item in s:#     print(item)tree=createTree(dataset,labels)testSet=createTestSet()print(predictAll(tree,labels,testSet))
····························································
输出：
['N', 'N', 'Y', 'N', 'Y', 'Y', 'N']

补充：

记住公式！！！