在做信用评分卡研究时,除了用KS/AUC指标,还经常见到基尼系数(gini coefficient)。
gini系数通常被用来判断收入分配公平程度。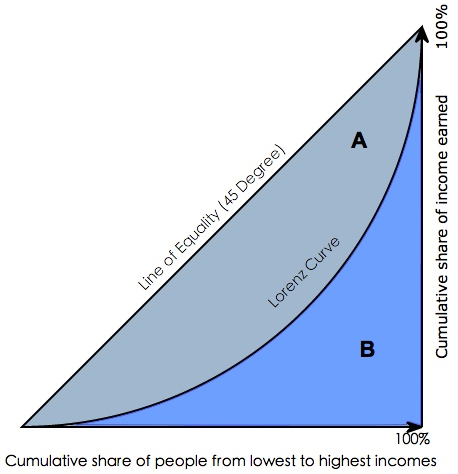
图.洛伦茨曲线与基尼系数
Gini coefficient 是指绝对公平线(line of equality)和洛伦茨曲线(Lorenz Curve)围成的面积与绝对公平线以下面积的比例,即gini coefficient = A面积 / (A面积+B面积) 。
但是,业界在实际计算Gini系数时往往用ROC曲线曲线和中线围成的面积与中线之上面积的比例,也就是Gini=2AUC-1。
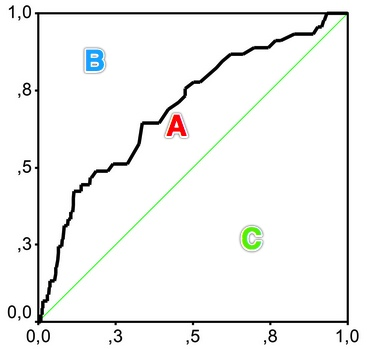
图.Gini coefficient与AUC
也就是说用ROC曲线去计算Gini的前提是ROC曲线和Gini曲线时重合的,因此Gini coefficient与AUC可以互相转换:
gini = A / (A + B) = (AUC - C) / (A + B) = (AUC -0.5) / 0.5 = 2*AUC - 1那问题来了,ROC曲线与Gini的洛伦兹曲线到底是不是重合的呢?
根据《信用风险评分卡研究》这本书中所说公式Gini=2AUC-1“只有在将ROC曲线解释为洛伦兹曲线时才成立”,而且“二者并不相同”。
下面仔细看下ROC曲线和洛伦兹曲线的异同点。
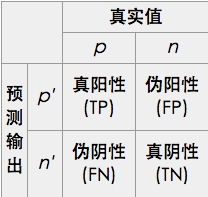
ROC空间是一个以伪阳性率(FPR, false positive rate)为X轴,真阳性率(TPR, true positive rate)为Y轴的二维坐标系所代表平面。
- TPR: 真阳性率,所有阳性样本中(TP+FN),被分类器正确判断为阳的比例。
TPR = TP / (TP + FN) = TP / 所有真实值为阳性的样本个数 - FPR: 伪阳性率,所有阴性样本中(FP+TN),被分类器错误判断为阳的比例。
FPR = FP / (FP + TN) = FP / 所有真实值为阴性的样本个数
洛伦兹曲线的纵轴是违约数占违约总量百分比的累计值,也就是TPR,而洛伦兹的横轴(被拒绝申请的百分比)是(FP+TP)/(TN+FP+FN+TP),当坏样本很少时,FN和TP的值很小,因而洛伦兹曲线和ROC曲线横纵轴取值基本一致,曲线基本重合。但当坏样本较多时,二者不重合,且差距较大。
最后的结论是:当样本中坏样本极少时可用gini=2AUC-1近似计算,当坏样本较多,或者好坏样本接近1:1时,那就得对gini单独计算比较准确。
最后是关于Gini值的计算:
(1) 用公式gini=2AUC-1
from sklearn import metrics
auc_roc_score = metrics.roc_auc_score(target_label, predict_probabilty)
gini_by_roc_score = 2 * auc_roc_score - 1(2) Gini的python直接计算可用下面文章中的代码:
https://blog.csdn.net/u010665216/article/details/78528261
def gini(actual, pred):
assert (len(actual) == len(pred))
all = np.asarray(np.c_[actual, pred, np.arange(len(actual))], dtype=np.float)
all = all[np.lexsort((all[:, 2], -1 * all[:, 1]))]
totalLosses = all[:, 0].sum()
giniSum = all[:, 0].cumsum().sum() / totalLosses
giniSum -= (len(actual) + 1) / 2.
return giniSum / len(actual)
def gini_normalized(actual, pred):
return gini(actual, pred) / gini(actual, actual)
gini_predictions = gini(actual, predictions)
ngini= gini_normalized(actual, predictions)