目录
画家算法的基本思想
多边形优先级的考虑
交叉覆盖和循环覆盖多边形的优先级考虑
解决深度优先级冲突的排序算法
画家算法的特点
画家算法的基本思想
先将画面中的物体按其距离观察点的远近进行排序,结果存放在一张线形表中。距观察点远者称其优先级高,放在表头,距观察点近者称其优先级低,放在表尾,这张表称为深度优先级表。
然后按照从表头到表尾的顺序逐个绘制物体。由于距观察者近的物体在表尾最后画出,它覆盖了远处的物体,最终在屏幕上产生了正确的遮挡关系。
画家算法看起来十分简单,但关键是如何对画面中各种不同情况下的多边形按深度排序,建立深度优先表。
假设视点在z轴正向无穷远处,视线方向沿着z轴负向看过去。如果z值大,离观察点近;而z值小,离观察点远。
多边形优先级的考虑
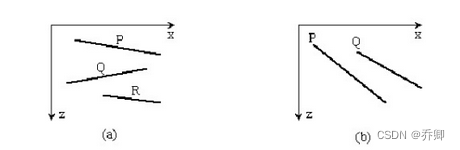
1、首先对一个简单的画面,如图(a)所示可以直接建立一个确定的深度优先表,排序可以一次完成,不会有任何的歧义。例如,多边形可按其最大或最小值排序,都可以很容易地把它们按深度大小分开。
2、但是,当画面略微复杂一点,如图(b)所示,却无法按简单的z向排序建立确定的深度优先表,以确定每一个多边形的优先级。例如,若按最小z坐标值(zmin)对P、Q排序,则在深度优先表中,P应排在Q之前,如按此顺序将P、Q写入帧缓冲器,则Q将部分地遮挡P。但实际上是P部分地遮挡Q。如果按最大z坐标值(zmax)对P、Q排序,同样也不能得到正确的消隐结果。
交叉覆盖和循环覆盖多边形的优先级考虑
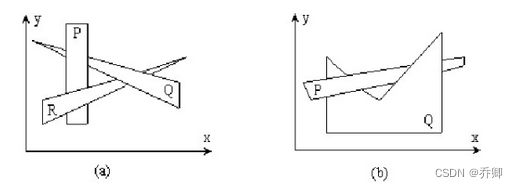
对更复杂的情况,如图所示,出现的困难更多。图(a)、(b)均有交叉覆盖或循环遮挡的情况。如在图(a)中,P在Q的前面,Q在R的前面,而R反过来又在P的前面。在图(b)中,P在Q的前面,而Q又在P的前面。对它们均无法直接建立确定的深度优先表。
解决深度优先级冲突的排序算法
假定视点在Z轴正向无穷远处,则该算法叙述如下:
1、计算多边形最小深度值zmin,并以此值的优先级进行排序,建立初步的深度优先表。表中第一个元素是对应有最小zmin值的多边形,标记为P,优先级最高。表中第二个多边形标记为Q。
2、考察P和Q之间的关系:
若P上离视点最近的顶点Pzmax比Q上离视点最远的顶点Qzmin还远,即QZmin≥Pzma,则P不遮挡Q,将P写入帧缓冲区,见图示。
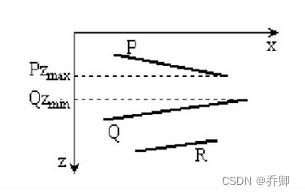
若Qzmin<Pzmax,那么P不但有遮挡Q的可能,而且还可能部分地遮挡表上Q之后的任一满足Rzmin<Pzmax的多边形R。我们把所有这种有可能被P所遮挡的多边形的全体记为{Q}。为了进一步确定P是否真正遮挡{Q}中的多边形,做以下逐步的测试,如果对{Q}中每个Q,都能通过以下问题中任一个,那么P不会遮挡{Q},因而可将P写入帧缓冲区中去。
所提出的问题是:
①P和Q的外接最小包围盒在X方向不相交吗?
②P和Q的外接最小包围盒在Y方向不相交吗?
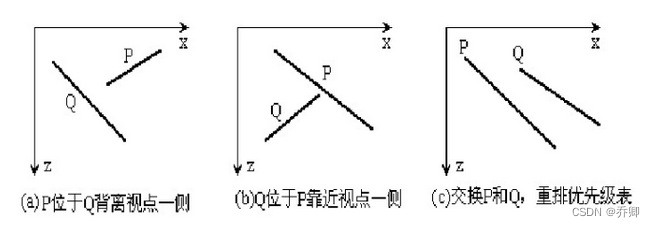
③P是否全部位于Q所在平面的背离视点的一侧。下图(a)能通过这一测试。
④Q是否全部位于P所在平面的靠近视点的一侧。下图(b)能通过这一测试。
⑤P和Q在显示屏幕上的投影是否可以分离。
若{Q}和P不能通过以上测试,就不能把P写到帧缓冲区中去,则交换P和Q,并将Q作上记号,形成新的优先级表。
3、 对重新排列的表重复2中步骤,对于图(c),经重新排列后,就能把Q写入帧缓冲区中去了。
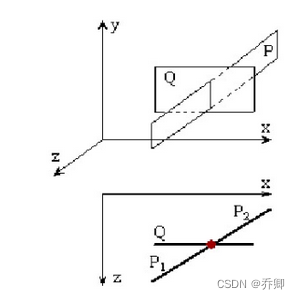
4、 执行3以后,若Q的位置需再次交换,则表明存在交叉覆盖的情况,见下图所示,这时可将P沿Q所在平面分割成两部分P,和P2,从表中去掉原多边形P,而将P的这两个新的部分插入原表中的适当位置,使其仍保持按zmin排序的性质。对新形成的表,重新执行2。
画家算法的特点
画家算法同时在物体空间和图像空间中进行处理,即:
在物体空间中排序以确定优先级,显示结果在算法运行之际就要不断地写入图像空间的帧缓存区中。






