前言

随着模型规模的不断扩大，微调模型的所有参数（所谓full fine-tuning）的可行性变得越来越低。以GPT-3的175B参数为例，每增加一个新领域就需要完整微调一个新模型，代价和成本非常高！

论文：LORA: LOW-RANK ADAPTATION OF LARGE LANNGUAGE MODELS
代码：https://github.com/microsoft/LoRA

现有方案存在的问题

Adapter Tuning

简单来说，adapter就是固定原有的参数，并添加一些额外参数用于微调。上图中会在原始的transformer block中添加2个adapter，一个在多头注意力后面，另一个这是FFN后面。
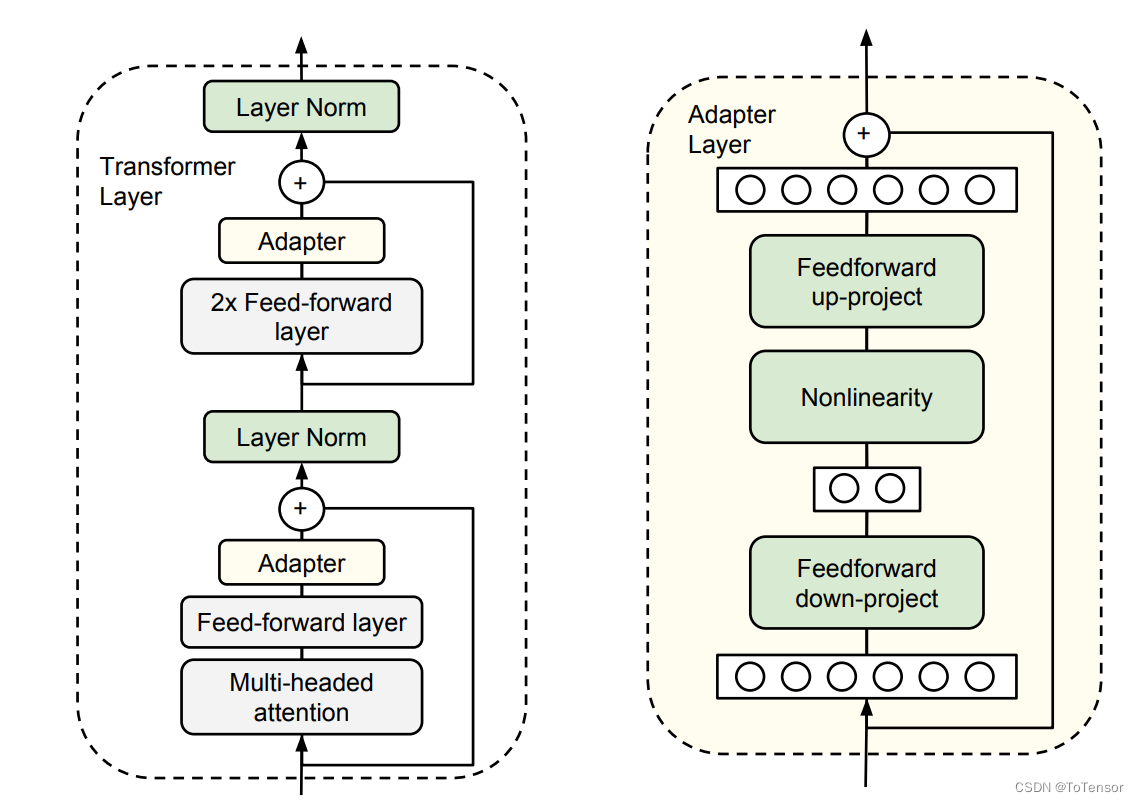
在这里插入图片描述
从图中可以看出，Adapter增加了模型的层数，导致模型推理速度变慢

Prefix Tuning

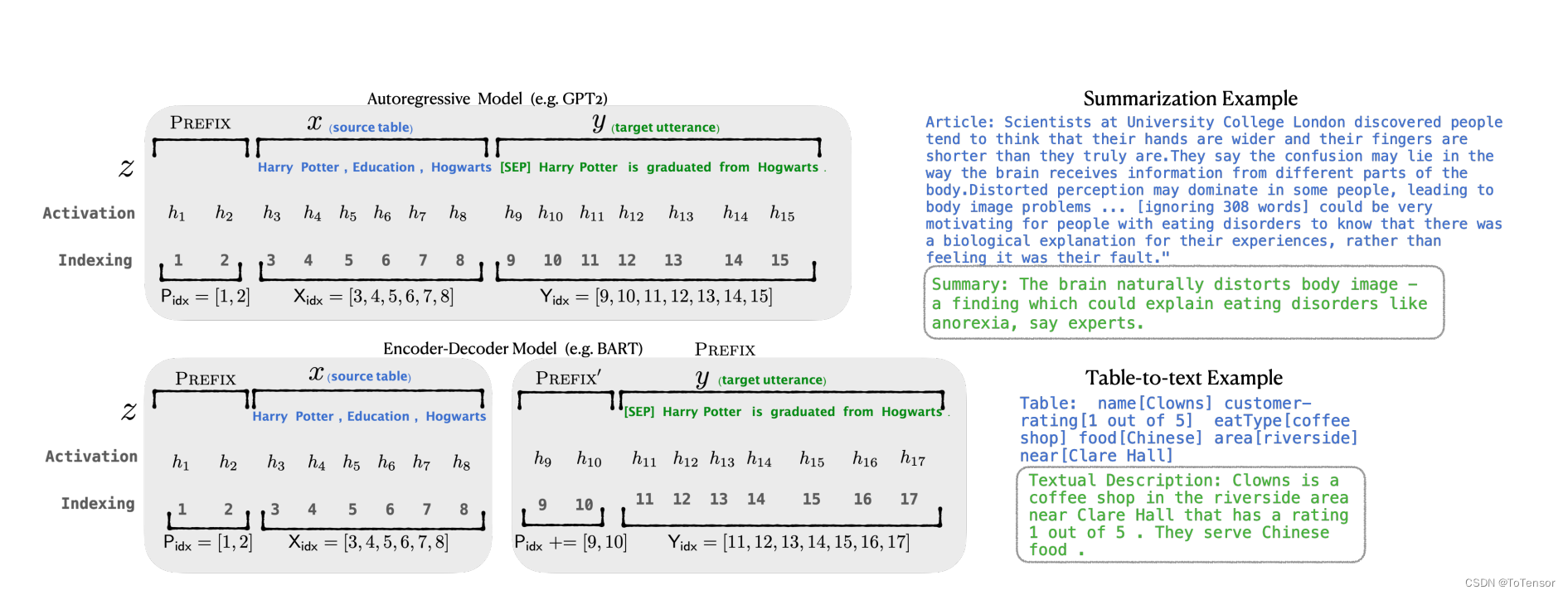
在这里插入图片描述

具体来说，对于transformer中的每一层，都在句子表征前面插入可训练的virtual token embedding。对于自回归模型(GPT系列)，在句子前添加连续前缀，即 Z = [PREFIX; x; y].
对于Encoder-Decoder模型(T5)，则在Ecoder和Decoder前都添加连续前缀 Z = [PREFIX; x | PREFIX; y].
添加前缀的过程如上图

虽然，prefix-tuning并没有添加太多的额外参数；但是，prefix-tuning难以优化，且会减少下游任务的序列长度。

LoRA

LoRA的两个关键优势：

预训练的模型可以共享，节省硬盘开销
切换任务时，只需要更换LoRA权重，成本低
训练时只需训练LoRA权重，内存消耗低

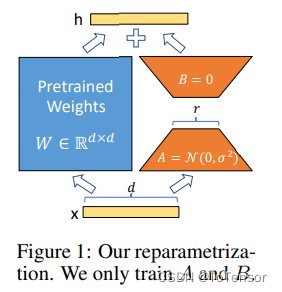
在这里插入图片描述
简单理解：在模型的Linear层的旁边，增加一个“旁支”，这个“旁支”的作用，就是代替原有的参数矩阵W进行训练。

结合上图，我们来直观地理解一下这个过程，输入 $x$ ，具有维度 $d$ ，举个例子，在普通的transformer模型中，这个 $x$ 可能是embedding的输出，也有可能是上一层transformer layer的输出，而 $d$ 一般就是768(大多数Bert的输出维度是768)。按照原本的路线，它应该只走左边的部分，也就是原有的模型部分。

而在LoRA的策略下，增加了右侧的“旁支”，也就是先用一个Linear层A，将数据从 $d$ 维降到 $r$ 维，这个 $r$ 也就是LORA的秩，是LoRA中最重要的一个超参数。一般会远远小于 $d$ (见的比较多的是4、8)，尤其是对于现在的大模型， $d$ 已经不止是768或者1024，例如LLaMA-7B，每一层transformer有32个head，这样一来 $d$ 就达到了4096.

接着再用第二个Linear层B，将数据从 $r$ 变回 $d$ 维。最后再将左右两部分的结果相加融合，就得到了输出的hidden_state。

对于左右两个部分，右侧看起来像是左侧原有矩阵 $W$ 的分解，将参数量从 $d * d$ 变成了 $d * r + r * d$ ，也就是 $2 * d * r$ ，在 $r << d$ 的情况下，参数量就大大地降低了。

在Albert中，作者考虑到词表的维度很大，所以将Embedding矩阵分解成两个相对较小的矩阵，用来模拟Embedding矩阵的效果，这样一来需要训练的参数量就减少了很多。(实际上也就减少了10M左右，Albert参数量较少的主要原因跨层参数共享)
在这里插入图片描述
LoRA也是类似的思想，并且它不再局限于Embedding层，而是所有出现大矩阵的地方，理论上都可以用到这样的分解。

但是与Albert不同的是，Albert直接用两个小矩阵替换了原来的大矩阵，而LoRA保留了原来的矩阵W，但是不让W参与训练，所以需要计算梯度的部分就只剩下旁支的A和B两个小矩阵。

从论文中的公式来看，全参微调时，模型训练的优化表示为（以自回归语言模型为例）：
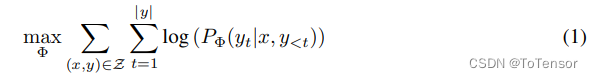
在这里插入图片描述
即最大化条件概率

其中，模型的参数用 $\Phi$ 表示。

全参微调的一个主要缺点是，对于每个下游任务，都需要学习一组不同的参数，如果预训练的模型很大，如GPT3（1750亿参数），存储和部署许多独立的微调模型实例可能是一项挑战。

而加入了LoRA之后，模型的优化表示为：
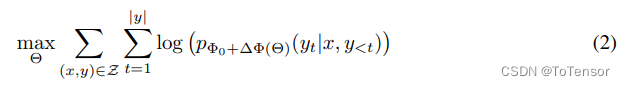
在这里插入图片描述
其中，模型原有的参数是 $\Phi_0$ ，LoRA新增的参数是 $\Delta \Phi\left(\Theta\right)$ 。

从第二个式子可以看到，尽管参数看起来增加了（多了 $\Delta \Phi\left(\Theta\right)$ ），但是从前面的max的目标来看，需要优化的参数只有 $\Theta$ ，而根据假设， $\Phi$ ，这就使得训练过程中，梯度计算量少了很多，所以就在低资源的情况下，我们可以只消耗 $\Theta$ 这部分的资源，这样一来就可以在单卡低显存的情况下训练大模型了。