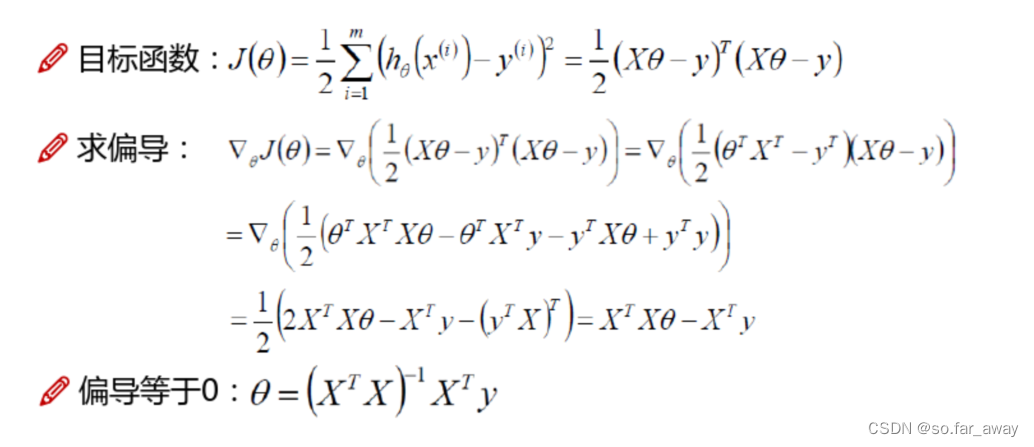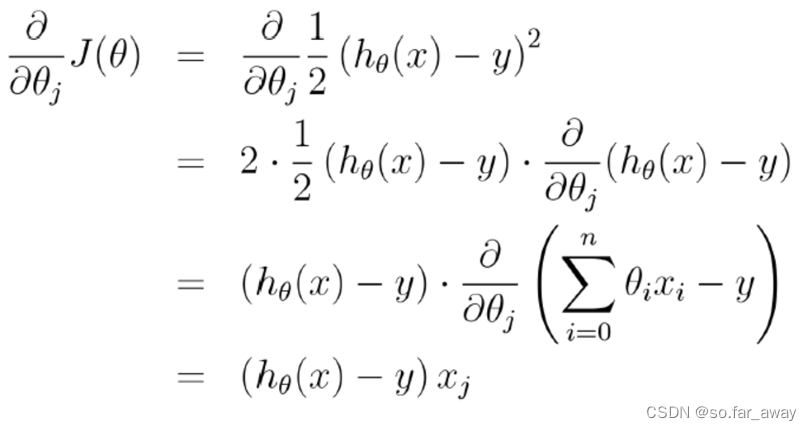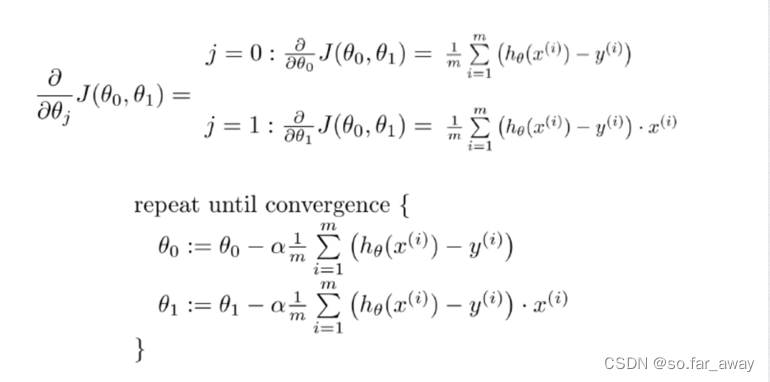算法概述

• 回归就是用一条曲线对数据点进行拟合，该曲线称为最佳拟合曲线，这个拟合过程称为回归。当该曲线是一条直线时，就是线性回归。
• 线性回归（Linear Regression）是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖关系的一种统计分析方法。
• “线性”指一次，“回归”实际上就是拟合。线性回归一般用来做连续值的预测，预测的结果是一组连续值。在训练学习样本时，不仅需要提供特征向量X，还需要提供样本的实际结果（标记label），因此线性回归模型属于监督学习里的回归模型。

最小二乘法

一元线性回归

• 回归分析用来建立方程模拟两个或多个变量之间如何关联。
• 被预测的变量叫做：因变量，输出。
• 被用来进行预测的变量叫做：自变量，输入。
• 一元线性回归包括一个自变量和一个因变量。
• 以上两个变量的关系用一条直线来模拟。
• 如果包含两个以上的自变量，则称为多元回归分析。
  $h_{\theta }(x)={\theta }_0+{\theta }_{1}x$
  这个方程对应的图像是一条直线，称作回归线。其中，${\theta }_1$是回归线的斜率，${\theta }_0$是回归线的截距。

求解方程系数

线性回归试图学得$h_{\theta }(x_i)={\theta }_1{x}_i+{\theta }_0$，使得$h_{\theta }(x_i)\approx y_i$，如何确定${\theta }_1,{\theta }_0$，关键在于如何减小$h_{\theta }(x_i)$与y的差别。
基于均方差最小化来进行模型求解的方法称为“最小二乘法”(least square method)。在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。

代价函数

真实值y，预测值$h_{\theta }(x)$，则误差平方为$(y-h_{\theta }(x){)}^2$。
找到合适的参数，使得误差平方和：
$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(y_i-h_{\theta }(x_i){)}^2$$最小。

最小二乘法求解系数

令目标函数对${\theta }_1$和${\theta }_0$的偏导为零可解得：
$$\{\begin{array}{l}{\theta }_1=\frac{{\sum }_{i=1}^m{y}_i(x_i-\overline{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\\ \\ {\theta }_0=\frac{1}{m}{\sum }_{i=1}^m(y_i-{\theta }_1{x}_i)\end{array}$$

多元线性回归

• 可以将b同样看作权重，即：
  $$\{\begin{array}{l}\vec{\omega }=（{\omega }_1，{\omega }_2，...，{\omega }_n，b）\\ \vec{x}=（x^1，x^2，...，x^n，1）\end{array}$$
• 此时$y\approx f(x)={\vec{\omega }}^T\vec{x}$，优化目标为$minJ(\omega )=min(Y-X\omega )(Y-X\omega )$，其中Y为样本矩阵的增广矩阵，X为对应的标签向量：
  $$\left[\begin{array}{cccccc}{x}_1^1& x_1^2& x_1^3& \cdots & x_1^n& 1\end{array}\right]$$
  $$\left[\begin{array}{cccccc}{x}_1^1& x_1^2& x_1^3& \cdots & x_1^n& 1\\ x_2^1& x_2^2& x_2^3& \cdots & x_2^n& 1\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ x_m^1& x_m^2& x_m^3& \cdots & x_m^n& 1\end{array}\right]$$
  $$Y=(y_1,y_2,...,y_n{)}^T$$
• 求解优化目标可得 ：
  $$\vec{\omega }=(X^{T}X{)}^{-1}{X}^{T}X$$
• 当$X^{T}X可逆时，线性回归模型存在唯一解。$

举例

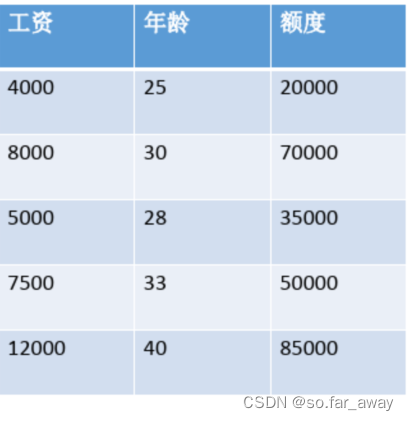
数据：工资和年龄（2个特征）
目标：预测银行会贷款给我多少钱（标签）
考虑：工资和年龄都会影响最终银行贷款的结果，那么它们各自有多大的影响呢？（参数）

分析：X1,X2就是我们的两个特征（年龄，工资），Y是银行最终会借给我们多少钱。我们需要找到最合适的一条线（想象一个高维）来最好地拟合我们的数据点。
解决：

• 假设${\theta }_1$是年龄的参数，${\theta }_2$是工资的参数。
• 拟合的平面：$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$(${\theta }_0$是偏置项)
• 整合：$h_{\theta }(x)={\sum }_{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$
  

最小二乘法算法实现：

import numpy as np
from numpy import mat
import matplotlib.pyplot as plt
iter=50
#1，获得x,y数据
X=np.random.rand(iter)*20
noise=np.random.randn(iter)
y=0.5*X+noise
plt.scatter(X,y)
plt.show()
#2.矩阵形式转换X,Y
Y_mat=mat(y).T
#50行2列
X_temp=np.ones((iter,2))
X_temp[:,0]=X
X_mat=mat(X_temp)
#3.利用解析法 p=(X^TX)^-1X^TY
pamaters=(((X_mat.T)*X_mat).I)*X_mat.T*Y_mat#权重矩阵
print(pamaters)
#4.显示
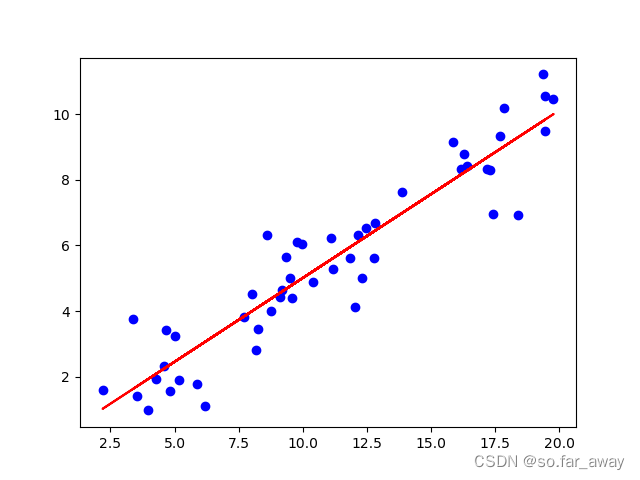
predict_Y=X_mat*pamaters#线性回归线
plt.figure()
plt.scatter(X,y,c='blue')
plt.plot(X,predict_Y,c='red')
plt.show()

实验结果：

权重矩阵：

算法应用

数据集介绍

波士顿房价数据集（Boston House Price Dataset）

• 波士顿房价数据集（Boston House Price Dataset）包含对房价的预测，以千美元计，给定的条件是房屋及其相邻房屋的详细信息。
• 该数据集是一个回归问题。每个类的观察值数量是均等的，共有 506 个观察，13 个输入变量和1个输出变量。
• sklearn库的datasets包含该数据集（ load_boston）。
• 调用方法：from sklearn import datasets。

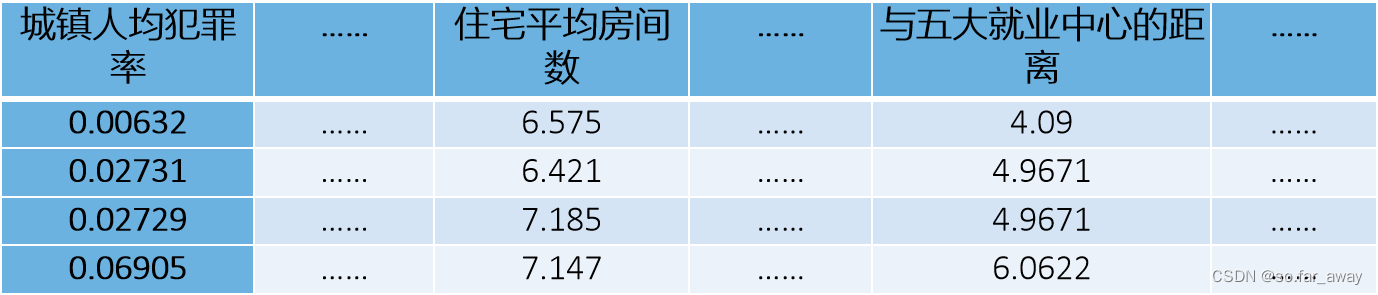
变量名说明：

• CRIM：城镇人均犯罪率。
• ZN：住宅用地超过 25000 sq.ft. 的比例。
• INDUS：城镇非零售商用土地的比例。
• CHAS：查理斯河空变量（如果边界是河流，则为1；否则为0）。
• NOX：一氧化氮浓度。
• RM：住宅平均房间数。
• AGE：1940 年之前建成的自用房屋比例。
• DIS：到波士顿五个中心区域的加权距离。
• RAD：辐射性公路的接近指数。
• TAX：每 10000 美元的全值财产税率。
• PTRATIO：城镇师生比例。
• B：1000（Bk-0.63）^ 2，其代中 Bk 指城镇中黑人的比例。
• LSTAT：人口中地位低下者的比例。
• MEDV：自住房的平均房价，以千美元计。

实现线性回归

sklearn.linear_model中的LinearRegression可实现线性回归
调用方法：from sklearn.linear_model import LinearRegression
LinearRegression的常用方法有：

• fit(X,y)：拟合模型
• predict(X)：求预测值

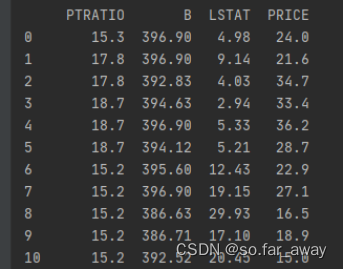
波士顿房价预测的部分数据：

直觉告诉我们：上表中住宅平均房间数与最终房价一般是成正比的，具有某种线性关系。我们利用线性回归法来验证想法。
同时，作为一个二维的例子，可以在平面上绘出图形，进一步观察图形。

算法实现

代码实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
#1.把数据转化成pandas的形式 在列尾加上房价PRICE
boston_dataset=load_boston()
data=pd.DataFrame(boston_dataset.data)
data.columns=boston_dataset.feature_names
print(data)
data['PRICE']=boston_dataset.target
#2.取出房间数和房价并转化成矩阵形式
x=data.loc[:,'RM'].as_matrix(columns=None)
y=data.loc[:,'PRICE'].as_matrix(columns=None)
#3.进行矩阵的转置
x=np.array([x]).T
y=np.array([y]).T
#4.训练线性模型
l=LinearRegression()
l.fit(x,y)
#5.画图显示
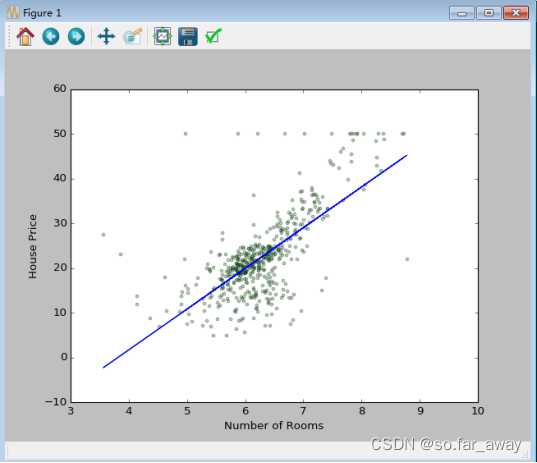
plt.scatter(x,y,s=10,alpha=0.3,c='green')
plt.plot(x,l.predict(x),c='blue',linewidth='1')
plt.xlabel('Number of Rooms')
plt.ylabel('House Price')
plt.show()

注：这段代码是在学校的机房实现的，python版本较低，实现过程中可能as_matrix()方法和load_boston()会有报错和提示。
数据集格式


预测结果：

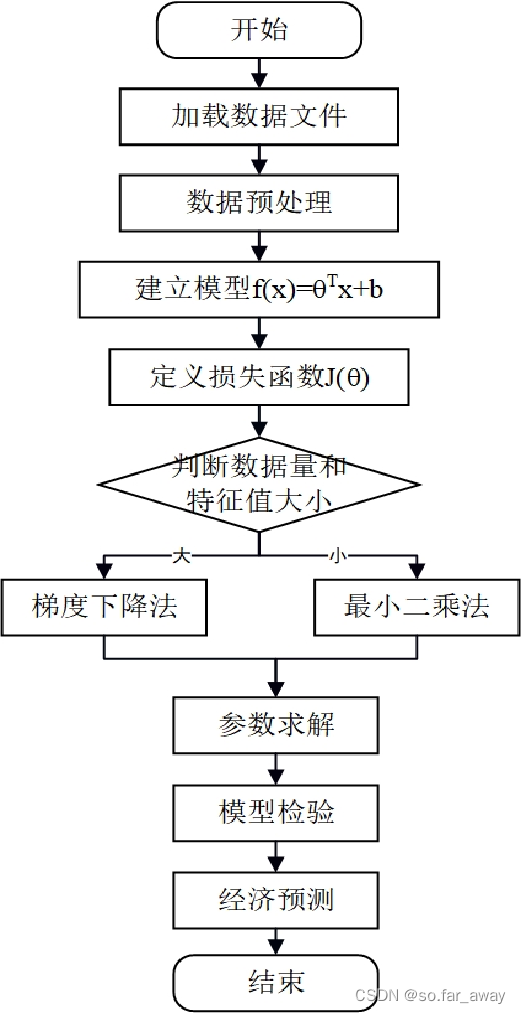
线性回归的算法流程

最小二乘法的局限性

首先，最小二乘法需要计算$X^{T}X$的逆矩阵，有可能它的逆矩阵不存在，这样就没办法使用最小二乘法了。
第二，当样本特征非常多的时候，计算$X^{T}X$的逆矩阵是一个非常耗时的工作，甚至不可行。
第三，如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用。

梯度下降法

场景

• 引入：当我们得到一个目标函数后，如何进行求解？直接求解？（并不一定可解，线性回归可以当做是一个特例）
• 常规套路：机器学习的套路就是我交给机器一堆数据，然后告诉它什么样的学习方式是对的（目标函数），然后让它朝着这个方向去做。
• 如何优化：一口吃不成个胖子，我们需要静悄悄的一步步的完成迭代。（每次优化一点点，这就是梯度下降的本质）

梯度下降算法（Gradient Descent）

• 目标函数（误差）：$J(\theta )=\frac{1}{2}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
• 初始化$\theta$（随机初始化）
• 沿着负梯度方向迭代，更新后的$\theta$使得$J(\theta )$更小，即：
  $$\theta =\theta -\alpha \cdot \frac{\partial J(\theta )}{\partial \theta }$$$$\alpha ：学习率、步长$$
  
• 梯度方向：
  
  
• 小结：
  Have some function:$J({\theta }_0,{\theta }_1)$
  Want:$minJ({\theta }_0,{\theta }_1)$
  1）初始化${\theta }_0,{\theta }_1$
  2）不断改变${\theta }_0,{\theta }_1$，直到$J({\theta }_0,{\theta }_1)$到达一个全局最小值，或局部极小值（待会解释）。

算法实例

代码实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#1.获得x,y数据
iter=50
#50个随机种子
X=np.random.rand(iter)*20
noise=np.random.randn(iter)
y=0.5*X+noise
plt.scatter(X,y)
plt.show()
#2.初始化参数
w=np.random.randn(1)
b=np.zeros(1)
print(w,b)
#3.根据样本更新参数
lr=0.001
for iteration in range(40):#初始化拟合y_pred=w*X+b#梯度更新w_gradient=0b_gradient=0N=len(X)for i in range(N):w_gradient+=(w*X[i]+b-y[i])*X[i]b_gradient+=(w*X[i]+b-y[i])w-=lr*w_gradient/Nb-=lr*b_gradient/N#更新后拟合y_pred=w*X+b#显示plt.scatter(X,y,c='blue')plt.plot(X,y_pred,c='red')plt.pause(0.2)

实现效果：

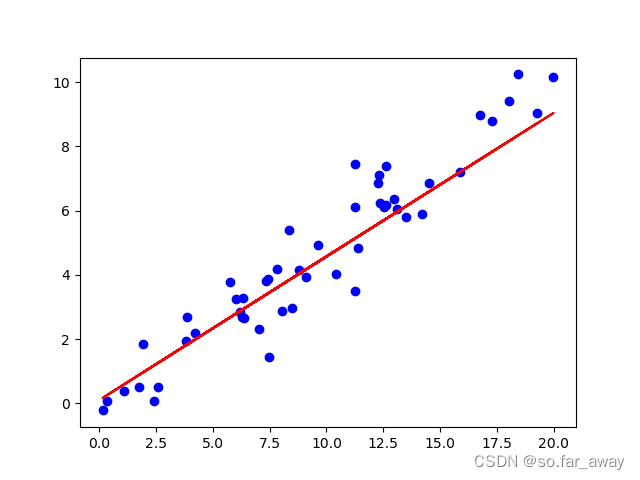
梯度下降法求极值的主要问题

1.梯度下降中的超参数设置
上面的梯度下降中提到了一个参数 ɑ，它又称为步长。这种算法是需要人为设置的，而非用来学习的参数，所以叫做超参数。步长是梯度下降算法中最重要的超参数，设置时需要精心考虑。

学习率不能太大，也不能太小，可以多尝试一些值0.1，0.03，0.01，0.003，0.001，0.0003，0.0001…
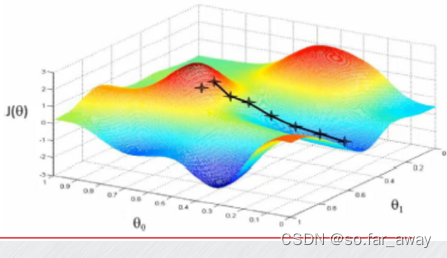
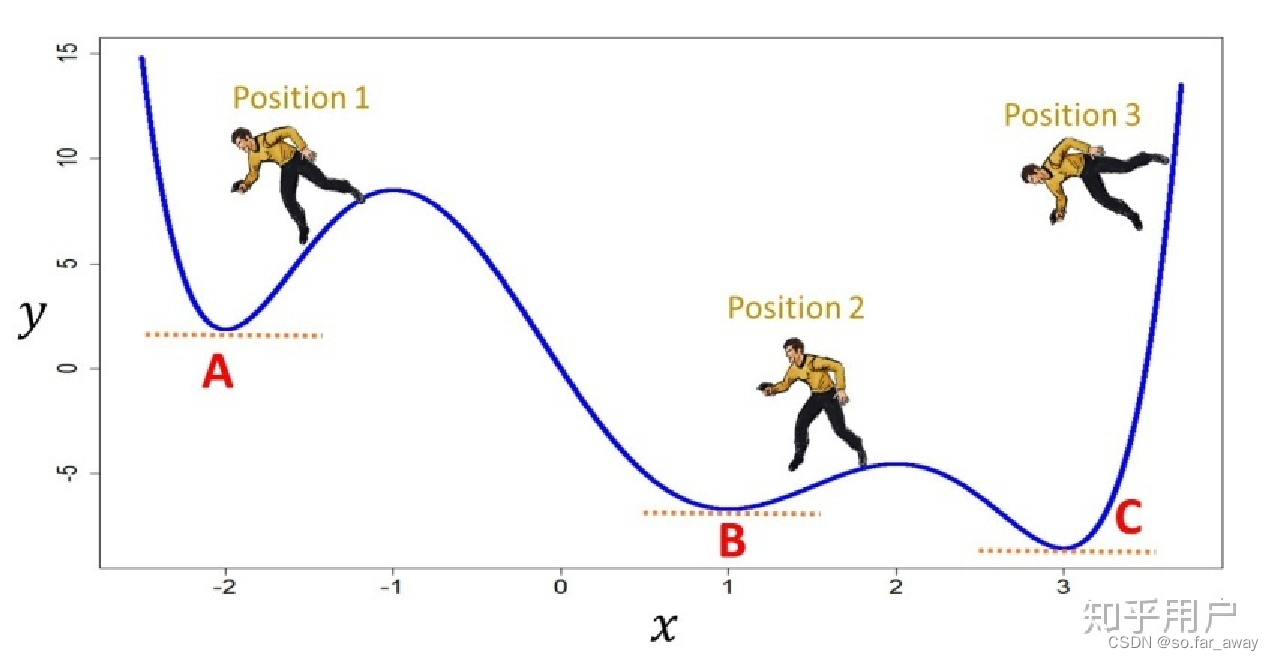
2.梯度下降问题
如果目标函数有多个极小值点（很多个低谷），那么如果开始位置不理想，很可能导致最终卡在一个局部极小值。比如下图的例子。这是梯度下降算法的一大挑战。

梯度下降的方式

梯度下降，目标函数：$J(\theta )=\frac{1}{2m}{\sum }_{i=1}^m(y^i-h_{\theta }(x^i){)}^2$

逻辑回归

引入

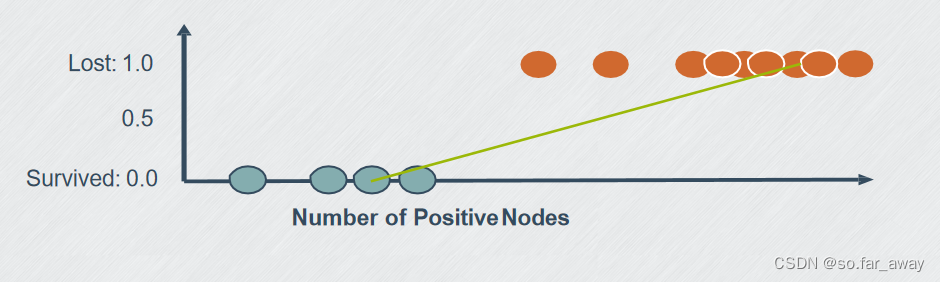
问题的提出——线性回归做分类？
癌症病人治疗5年之后的状况：

线性分类：将线性回归模型输出的连续值进行离散化。
构建线性分类器的关键：如何将线性回归模型输出的连续值取值进行离散化。
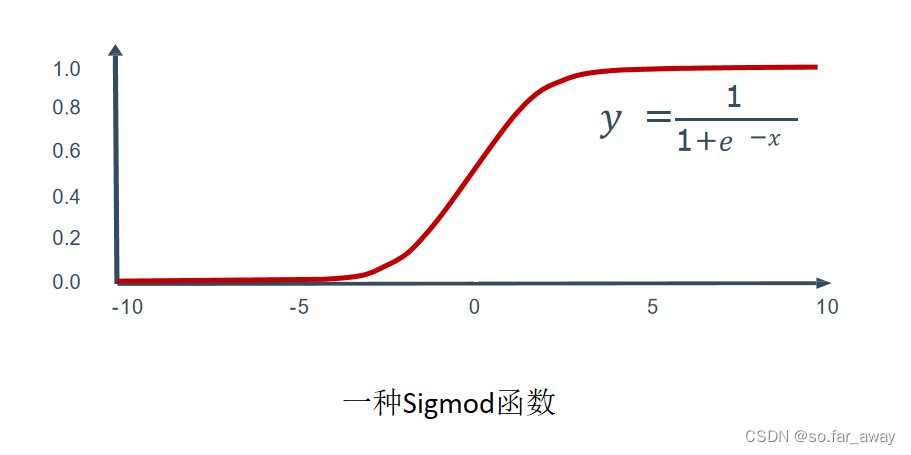
Logistic函数:

癌症病人治疗5年之后的状况：

逻辑回归与线性回归的关系

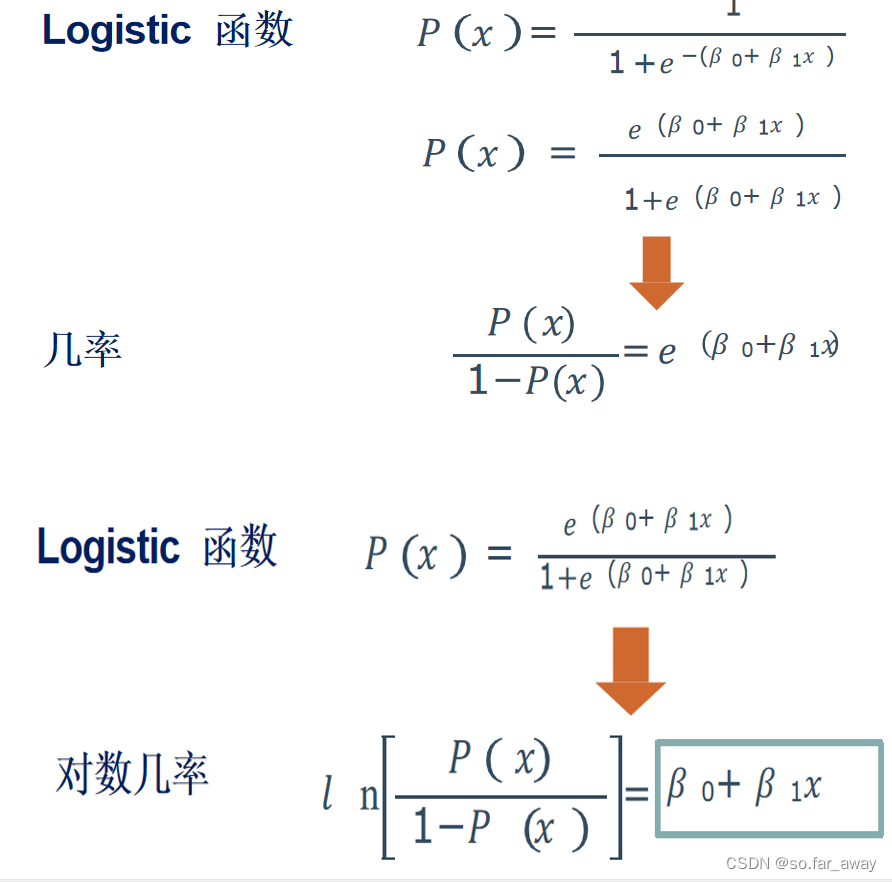
逻辑回归

线性回归的函数$h(x)=z={\omega }^{T}x+b$，范围是($-\infty ,+\infty$)。
而分类预测结果需要得到[0,1]的概率值。
在二分类模型中，事件的几率odds：事件发生与事件不发生的概率之比为$\frac{p}{1-p}$，称为事件的发生比。其中p为随机事件发生的概率，p的范围为[0,1]。
取对数得到：$ln\frac{p}{1-p}$，而$ln\frac{p}{1-p}={\omega }^{T}x+b$
求解得到：$p=\frac{1}{1+e^{-({\omega }^{T}x+b)}}$
为了方便描述，令：
$$\vec{\omega }=（{\omega }_1，{\omega }_2，......，{\omega }_n，b{）}^T$$$$\vec{x}=（x^1，x^2，......，x^n，1{）}^T$$

逻辑回归的求解过程

• 找一个合适的预测分类函数，用来预测输入数据的分类结果，一般表示为h函数，需要对数据有一定的了解或分析，然后确定函数的可能形式。
• 构造一个损失函数，该函数表示预测输出（h）与训练数据类别（y）之间的偏差，一般是预测输出与实际类别的差，可对所有的样本的Cost求R方值等作为评价标准，记为$J(\theta )$函数。
• 找到$J(\theta )$函数的最小值，因为值越小表示预测函数越准确。求解损失函数的最小值是采用梯度下降法实现。

逻辑回归的语法

• 导入包含分类方法的类：
  from sklearn.linear_model import LogisticRegression
• 创建该类的一个实例：
  LR=LogisticRegression(penalty='12',C=10.0)
• 拟合训练数据并预测：
  LR=LR.fit(X_train,y_train)
y_predict=LR.predict(X_test)

评价指标

混淆矩阵

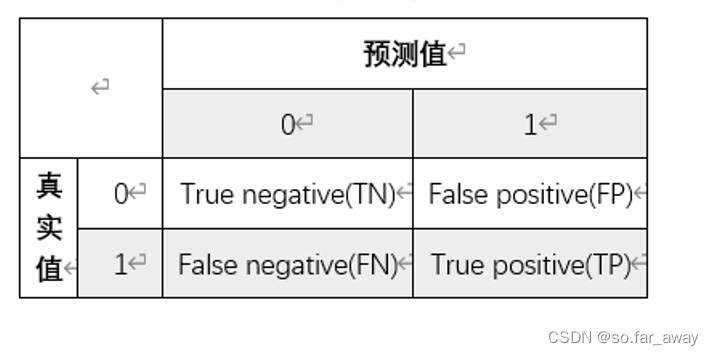
混淆矩阵是理解大多数评价指标的基础，这里用一个经典表格来解释混淆矩阵是什么：

混淆矩阵包含了四部分信息：
1）真阴性（TN）表明实际是负样本预测成负样本的样本数。
2）假阳性（FP）表明实际是负样本预测成正样本的样本数。
3）假阴性（FN）表明实际是正样本预测成负样本的样本数。
4）真阳性（TP）表明实际是正样本预测成正样本的样本数。
大部分的评价指标都是建立在混淆矩阵基础上的，包括准确率、精确率、召回率、FI-score，当然也包括AUC。

准确率

• 准确率是最为常见的一个指标，即预测正确的结果占总样本的百分比，其公式如下：
  $$accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
• 虽然准确率可以判断总的正确率，但是在样本不平衡的情况下，并不能作为很好的指标来衡量结果。假设在所有样本中，正样本占90%，负样本占10%，样本是严重不平衡的。模型将全部样本预测为正样本即可得到90%的高准确率，如果仅使用准确率这一单一指标，模型就可以像这样偷懒获得很高的评分。正因如此，也就衍生出了其它两种指标：精确率和召回率。

精确率

• 精确率又叫查准率，它是针对预测结果而言的。精确率表示在所有被预测为正的样本中实际为正的样本的概率。意思就是在预测为正样本的结果中，有多少把握可以预测正确，公式如下：
  $$precision=\frac{TP}{TP+FP}$$
• PR曲线是以查准率为纵坐标，以查全率为横坐标做出的曲线，如图：
  

召回率

• 召回率又叫查全率，它是针对原样本而言的。召回率表示在实际为正的样本被预测为正样本的概率，公式如下：
  $$recall=\frac{TP}{TP+FN}$$
• 召回率一般应用于宁可错杀一千，绝不放过一个的场景下。例如在网贷违约率预测中，相比信誉良好的用户，我们更关心可能会发生违约的用户。召回率越高，代表不良用户被预测出来的概率越高。

scikit-learn库函数

1.accuracy_score:用于评价分类问题的准确率。函数原型为：
sklearn.metrics.accuracy_score(y_true,y_pred,normalize=True,sample_weight=None)
参数如下（了解）：

• y_true：样本集的真实标记集合。
• y_pred：分类器对样本集预测的预测值。
• normalize：默认值为True。如果为True，则返回分类正确的比例（准确率），否则返回分类正确的数量。
• sample_weight：样本权重，默认每个权重都相等（取值1）。

2.precision_score:用于评价分类问题的查准率。函数原型为：
sklearn.metrics.precision_score(y_true,y_pred,labels=None,pos_label=1,average='binary',sample_weight=None)
参数详解（了解）：

• labels：当average!='binary'时，则包括标签集。
• pos_label：字符串或整数，默认值为1。指定哪个标记值为正类。
• average：字符串。多标签目标需要此参数。如果为None，则返回每个类的得分，否则，这将确定对数据执行的平均类型：binary、micro、macro、weighted、samples。
  返回值：浮点型，分类精度。

3.recall_score：用于计算分类结果的召回率。函数原型为：
sklearn.metrics.recall_score(y_true,y_pred,labels=None,pos_label=1,average='binary',sample_weight=None)

4.classification_report：以文本的方式给出分类结果的主要预测性能指标。函数原型为：
sklearn.metrics.classification_report(y_true,y_pred,labels=None,target_names=None,sample_weight=None,digits=2)

案例：基于逻辑回归实现乳腺癌预测

代码实现：

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
cancer=load_breast_cancer()
#导入训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(cancer.data,cancer.target,test_size=0.2)
model=LogisticRegression()
#训练
model.fit(X_train,y_train)
#在训练集上的准确率
train_score=model.score(X_train,y_train)
#在测试集上的准确率
test_score=model.score(X_test,y_test)
print('train score:{train_score:.6f}; test score:{test_score:.6f}'.format(train_score=train_score,test_score=test_score))

实验结果：

评价模型在测试集上的准确率、精确率、召回率：
代码实现：

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
cancer=load_breast_cancer()
#导入训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(cancer.data,cancer.target,test_size=0.2)
model=LogisticRegression()
#训练
model.fit(X_train,y_train)
#在训练集上的准确率
train_score=model.score(X_train,y_train)
#在测试集上的准确率
test_score=model.score(X_test,y_test)
# print('train score:{train_score:.6f}; test score:{test_score:.6f}'.format(train_score=train_score,test_score=test_score))
y_pred=model.predict(X_test)
#混淆矩阵中的准确率：也就是总的正确率
accuracy_score_value=accuracy_score(y_test,y_pred)
#召回率：表示在实际为正的样本中被预测为正样本的概率
recall_score_value=recall_score(y_test,y_pred)
#精确率：表示在所有被预测为正的样本中实际为正的样本的概率，也就是说在预测为正样本的结果中，有多少把握可以预测正确
precision_score_value=precision_score(y_test,y_pred)
#以文本的形式给出分类结果的主要预测性能指标
classification_report_value=classification_report(y_test,y_pred)
print("准确率：",accuracy_score_value)
print("召回率：",recall_score_value)
print("精确率：",precision_score_value)
print(classification_report_value)

实验效果：