该算法题分别是：
118. 杨辉三角。
119. 杨辉三角 II

1 [杨辉三角]

1.1 给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

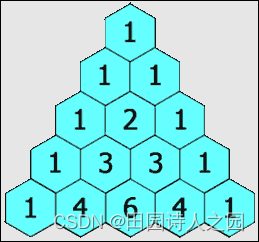
1.2 示例

1.2.1 示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

1.2.2 示例 2:

输入: numRows = 1
输出: [[1]]

1.2.3 提示:

1 <= numRows <= 30

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/pascals-triangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

1.3 算法解决方法

1.3.1 算法解题思路

1.3.1.1 确定状态

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

1.3.1.2 转移方程

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

1.3.1.3 初始条件以及边界情况

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

初始条件：
dp[0][0] = 1

边界情况：
dp[i][0] = dp[i][i] = 1;

1.3.1.4 计算顺序

dp[0][0]
dp[1][0]，dp[1][1]
…
dp[N - 1][0]，dp[N - 1][N - 1]

1.3.2 算法实现

class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> dp(numRows);for(int i = 0; i < numRows; i++) {dp[i].resize(i + 1);dp[i][0] = dp[i][i] = 1;}for (int i = 2; i < numRows; i++) {for (int j = 1; j < i; j++)dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}return dp;}
};

2 [杨辉三角 II]

2.1 给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

2.2 示例

2.2.1 示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

2.2.2 示例 2:

输入: rowIndex = 0
输出: [1]

2.2.3 示例 3:

输入: rowIndex = 1
输出: [1,1]

2.2.4 提示:

0 <= rowIndex <= 33

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/pascals-triangle-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2.3 算法解决方法

杨辉三角 II完全可以借助于上面的杨辉三角的解决方法去处理，不同的是要处理index和杨辉三角的关系，最后返回特定行的杨辉三角数据就可以。

2.3.1 算法解题思路

2.3.1.1 确定状态

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

2.3.1.2 转移方程

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

2.3.1.3 初始条件以及边界情况

• 设dp[i][j]表示第1 + 1行，第j + 1列的数
  dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];

初始条件：
dp[0][0] = 1

边界情况：
dp[i][0] = dp[i][i] = 1;

2.3.1.4 计算顺序

dp[0][0]
dp[1][0]，dp[1][1]
…
dp[N - 1][0]，dp[N - 1][N - 1]

返回第N- 1行的数据：
dp[N - 1][0]，dp[N - 1][N - 1]

2.3.2 算法实现

class Solution {
public:vector<int> getRow(int rowIndex) {int numRows = rowIndex + 1;vector<vector<int>> dp(numRows);for(int i = 0; i < numRows; i++) {dp[i].resize(i + 1);dp[i][0] = dp[i][i] = 1;}for (int i = 2; i < numRows; i++) {for (int j = 1; j < i; j++)dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];}return dp[rowIndex];}
};