2211. 统计道路上的碰撞次数（栈 || 脑筋急转弯）

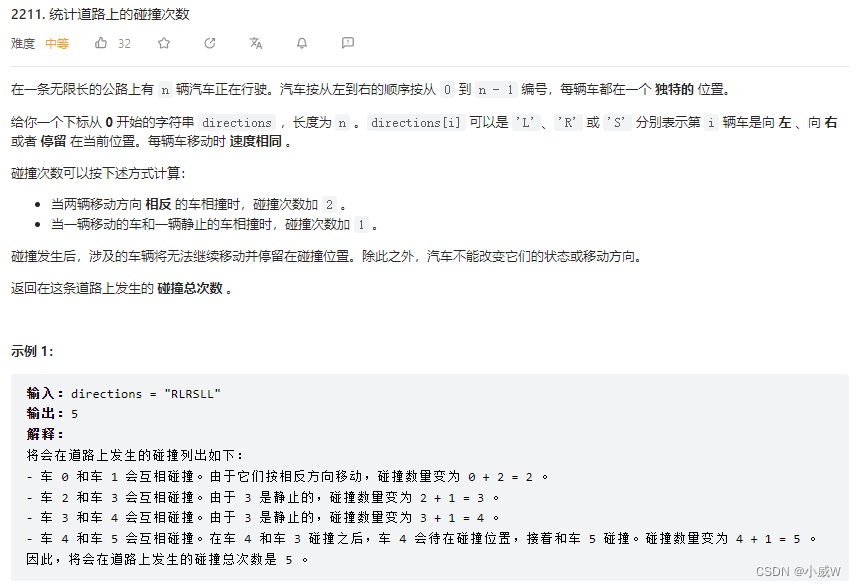
2211. 统计道路上的碰撞次数

难度：1581

提示：

1 <= directions.length <= 10^5
directions[i] 的值为 'L'、'R' 或 'S'

解法1：自己想的——使用栈

受 2126. 摧毁小行星 这道题的启发，使用栈来处理这个问题。

当枚举到 ‘R’ 和 ‘S’ 时，先放入栈中不做处理；
当枚举到 ‘L’ 时，如果此时栈中不为空，那么它会发生碰撞并停下来，因此 ans ++ ，并放入栈中一个 ‘S’;

枚举完毕后，再来处理栈中的 ‘R’，只要 ‘R’ 的上方有 ‘S’ 存在，就会贡献一个 ans ++。

class Solution {public int countCollisions(String directions) {Deque<Character> stk = new ArrayDeque();int ans = 0;for (char ch: directions.toCharArray()) {if (ch == 'L') {if (!stk.isEmpty()) {stk.push('S');++ans;}} else stk.push(ch);}boolean f = false;while (!stk.isEmpty()) {char ch = stk.pop();if (ch == 'R' && f) ++ans;if (ch != 'R') f = true;}return ans;}
}

时间复杂度是 $O(n)$

解法2——思维：去掉左右两边往左右开的车

去掉往左右两边开的车之后，剩下非停止的车必然会碰撞。

代码写法1——找左右端点

分别找到两边去掉之后的端点，枚举端点范围内的车辆，每个 L 和 R 都会贡献一个答案 ans++。

class Solution {public int countCollisions(String directions) {int n = directions.length(), l = 0, r = n - 1, ans = 0;while (l < n && directions.charAt(l) == 'L') ++l;while (r >= 0 && directions.charAt(r) == 'R') --r;for (int i = l; i <= r; ++i) {if (directions.charAt(i) != 'S') ++ans;}return ans;}
}

代码写法2——正则表达式去除+流处理api

class Solution {public int countCollisions(String s) {// 前缀向左的车不会发生碰撞s = s.replaceAll("^L+", ""); // 后缀向右的车不会发生碰撞s = new StringBuilder(s).reverse().toString().replaceAll("^R+", ""); // 剩下非停止的车必然会碰撞return s.length() - (int) s.chars().filter(c -> c == 'S').count(); }
}

补充：replaceAll() 和 正则表达式

Java 中的 String 类的 replaceAll() 方法是用来使用给定的 replacement 字符串替换此字符串匹配给定的正则表达式的每个子字符串。
它的语法是：

public String replaceAll(String regex, String replacement)

其中，regex 是要替换的正则表达式，replacement 是用来替换每个匹配项的字符串。

关于正则表达式：

更多关于正则表达式可见：正则表达式 - 廖雪峰的官方网站

本题中用到的 ^L+ 表示 匹配 1 个或多个位于字符串开头的 L。

补充：(int) s.chars().filter(c -> c == ‘S’).count(); 解释

对应代码中的这一句：

return s.length() - (int) s.chars().filter(c -> c == 'S').count(); 

由于解释太长，已经放在了：【Java语法小记】求字符串中某个字符的数量——IntStream流的使用 中。

2227. 加密解密字符串 （逆向思维）

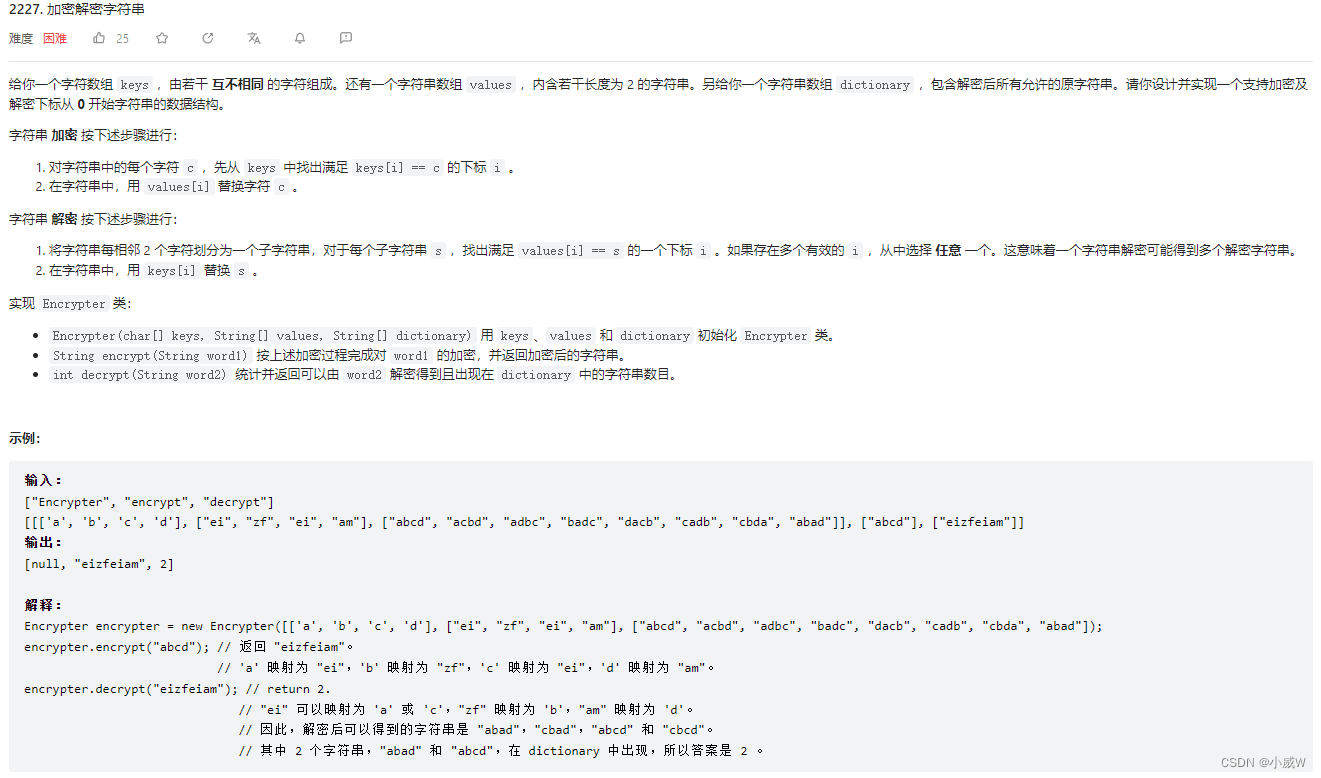
2227. 加密解密字符串

难度：1944

提示：

1 <= keys.length == values.length <= 26
values[i].length == 2
1 <= dictionary.length <= 100
1 <= dictionary[i].length <= 100
所有 keys[i] 和 dictionary[i] 互不相同
1 <= word1.length <= 2000
1 <= word2.length <= 200
所有 word1[i] 都出现在 keys 中
word2.length 是偶数
keys、values[i]、dictionary[i]、word1 和 word2 只含小写英文字母
至多调用 encrypt 和 decrypt 总计 200 次

思路

读懂题就已经很难了！

它初始给的代码框架长这样：

class Encrypter {public Encrypter(char[] keys, String[] values, String[] dictionary) {}public String encrypt(String word1) {}public int decrypt(String word2) {}
}

我们要填写构造方法、加密方法 和 计算解密后的数量方法。

思路：

• 构造方法用来定义一些会被使用到的数据结构。
• 加密方法按照题目要求进行模拟即可。
• 为了计算解密后出现在 dictionary 中字符串的数量，我们可以提前预处理出所有 dictionary 加密后的字符串并计数保存，这样在解密方法中直接查表就好了。

代码1

class Encrypter {char[] keys;String[] values, dictionary;Map<Character, Integer> m = new HashMap();Map<String, Integer> ans = new HashMap();public Encrypter(char[] keys, String[] values, String[] dictionary) {this.keys = keys;this.values = values;this.dictionary = dictionary;// 存储key中字符和对应的下标for (int i = 0; i < keys.length; ++i) m.put(keys[i], i);// 提前计算加密结果for (String d: dictionary) {String dd = encrypt(d);// 这里使用 dd + d.length() 作为键是为了确保我们找的加密前字符串的长度是解密前字符串长度的1/2，直接使用dd的话会被最后一个样例卡住// 即a对应bb,bbbb应该被解密成aa，但abb这个字符串加密之后也会成为bbbb影响答案计算ans.merge(dd + d.length(), 1, Integer::sum);}}public String encrypt(String word1) {StringBuilder ans = new StringBuilder();for (char ch: word1.toCharArray()) {if (m.containsKey(ch)) ans.append(values[m.get(ch)]);else ans.append(ch);}return ans.toString();}public int decrypt(String word2) {// 直接查表即可return ans.getOrDefault(word2 + (word2.length() / 2), 0);}
}

代码2

代码2的加密过程中，如果查询到了不在 key 中的字符，就会直接 return “” ，这样就使得加密过程产出的所有字符串都是全加密的（即字符串中的每个字符都映射成了新的字符串）。

这样也就避免了代码 1 注释中所说的问题：（

// 这里使用 dd + d.length() 作为键是为了确保我们找的加密前字符串的长度是解密前字符串长度的1/2，直接使用dd的话会被最后一个样例卡住
// 即a对应bb,bbbb应该被解密成aa，但abb这个字符串加密之后也会成为bbbb影响答案计算

）

而题目中的提示说明了 所有 word1[i] 都出现在 keys 中 ，所以不用担心这种写法对于加密结果的影响。

class Encrypter {Map<String, Integer> cnt = new HashMap();String[] map = new String[26];public Encrypter(char[] keys, String[] values, String[] dictionary) {// 记录字符c对应keys中下标i所在的values[i]for (int i = 0; i < keys.length; ++i) {map[keys[i] - 'a'] = values[i];}// 预处理dictionary加密for (String s: dictionary) {String e = encrypt(s);cnt.merge(e, 1, Integer::sum);}}public String encrypt(String word1) {StringBuilder res = new StringBuilder();for (char ch: word1.toCharArray()) {String s = map[ch - 'a'];if (s == null) return "";res.append(s);}return res.toString();}public int decrypt(String word2) {return cnt.getOrDefault(word2, 0);}
}

2242. 节点序列的最大得分⭐⭐⭐⭐⭐ （有技巧的枚举）

2242. 节点序列的最大得分

难度：2304

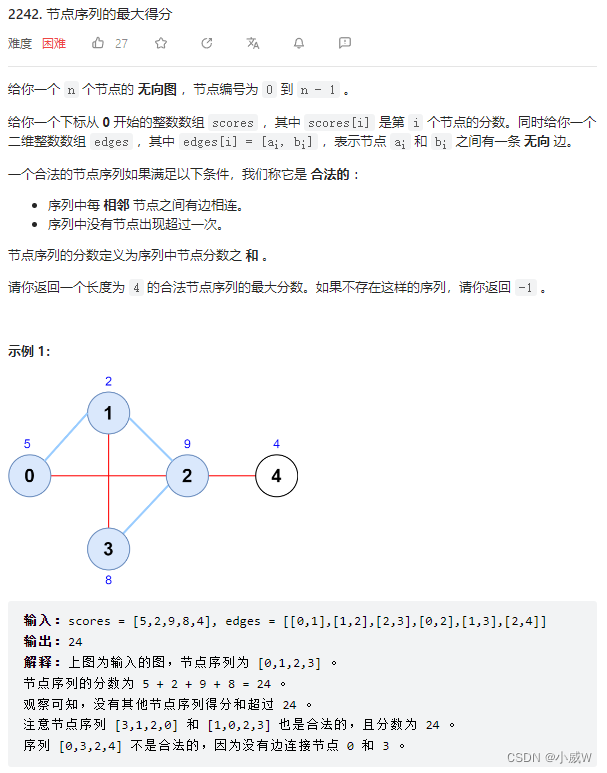
思路——有技巧的枚举（枚举中间的边）

Q：为什么枚举中间的边效率最好？
A：因为枚举一条边的同时就会确定两个点，这时只需要再对这两个点找到相邻最大的点就可以了。

代码

class Solution {public int maximumScore(int[] scores, int[][] edges) {int n = scores.length;List<int[]>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList());for (int[] edge: edges) {int x = edge[0], y = edge[1];g[x].add(new int[]{scores[y], y});g[y].add(new int[]{scores[x], x});}for (int i = 0; i < n; ++i) {// 如果和i相连的点的数量>3，就可以删掉只剩3个最大的// 这样删可以确保和它组成一个序列的另外3个值都不会被删掉// 即对于序列a-x-y-b,枚举到x的时候要保证a,y,b都不会被删掉// 删去其它的边是为了后面遍历的时候快一些if (g[i].size() > 3) {g[i].sort((a, b) -> (b[0] - a[0]));     // 按照score从大到小排序g[i] = new ArrayList<>(g[i].subList(0, 3));}}int ans = -1;// 枚举每个边作为中间的边for (int[] edge: edges) {int x = edge[0], y = edge[1];for (int[] p: g[x]) {int a = p[1];       // x旁边的节点号afor (int[] q: g[y]) {int b = q[1];   // y旁边的节点号bif (a != y && b != x && a != b) {ans = Math.max(ans, p[0] + q[0] + scores[x] + scores[y]);}}}}return ans;}   
}

2306. 公司命名⭐⭐⭐⭐⭐（分类讨论）

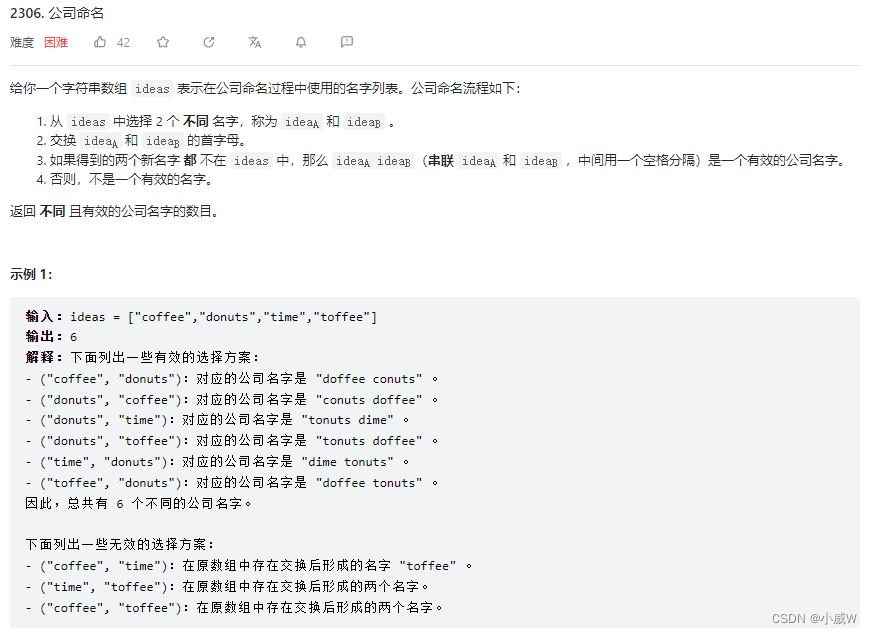
2306. 公司命名

难度：2305

提示：

2 <= ideas.length <= 5 * 10^4
1 <= ideas[i].length <= 10
ideas[i] 由小写英文字母组成
ideas 中的所有字符串 互不相同

从数据范围来看 $O(n^2)$ 的算法是不行的。

因此我们来考虑：

核心思想就是将每个字符串的首字符和其余部分分开，分组统计，分别计算出 有i无j 和 有j无i 的组的数量，最后计算答案。

class Solution {public long distinctNames(String[] ideas) {// 按照ideas[1:]分组,记录这个组的首字母有哪些(通过mask存储)Map<String, Integer> group = new HashMap();for (String idea: ideas) {String t = idea.substring(1);group.put(t, group.getOrDefault(t, 0) | 1 << (idea.charAt(0) - 'a'));}long ans = 0;int[][] cnt = new int[26][26];              // cnt[i][j]表示没i有j的组的个数for (int mask: group.values()) {// 计算cnt[i][j]for (int i = 0; i < 26; ++i) {for (int j = i + 1; j < 26; ++j) {if ((mask >> i & 1) == 0 && (mask >> j & 1) == 1) ++cnt[i][j];else if ((mask >> i & 1) == 1 && (mask >> j & 1) == 0) ++cnt[j][i];}}}// 所有成对的 cnt[i][j]和cnt[j][i] 可以贡献方案数for (int i = 0; i < 26; ++i) {for (int j = i + 1; j < 26; ++j) {ans += cnt[i][j] * cnt[j][i];}}return ans * 2;}
}

2317. 操作后的最大异或和（位运算）

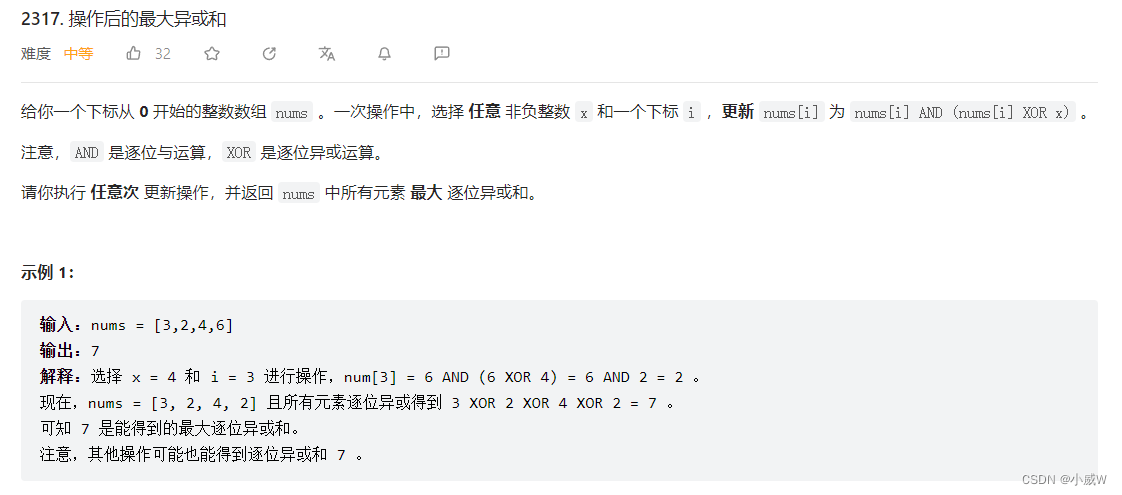
2317. 操作后的最大异或和

难度：1678

思路

先分析 nums[i] AND (nums[i] XOR x) 的结果：
由于是 AND ，所以 结果中 1 的数量一定小于 nums[i] 中 1 的数量；
由于 x 是任意取的，所以 nums[i] XOR x 可以获得任意数字，
因此 nums[i] AND (nums[i] XOR x) 的最终结果是可以删去 nums[i] 二进制表示中任意数量的 1。

我们知道异或的性质是：相同得0，不同得1
要想获得最大值，那就将尽可能多的位置上变成 1。
可以要想变成 1 ，就必须是 1 和 0 之间得异或，即这个位置上本来就有 1 ，我们就可以将其保留下来。

=》有 1 就保留 1 ，这是 或运算 的性质。

因此最终结果就是所有数字 或 起来的结果。

代码

class Solution {public int maximumXOR(int[] nums) {int ans = 0;for (int num: nums) ans |= num;return ans;}
}

相关链接