在上一篇文章中,我们介绍了单模光纤的一维模场分布,能看出沿着径向的光场分布情况,并分析能量的分布
这一篇中,我们绘制光纤横截面上的二维光场分布:代码如下:
clear
close all
V = 2.4000;
U = 1.6453;
W = 1.7473;Npoint = 21;
Rx = 2;
Ry = 2;
x = linspace(-Rx,Rx,Npoint);
y = linspace(-Ry,Ry,Npoint);
[X Y] = meshgrid(x,y);
R = sqrt(X.^2+Y.^2);E1 = besselj(0,U*R);
E2 = besselj(0,U).*besselk(0,W.*R)./besselk(0,W);
E = E1;
pos = find(R >= 1);
E(pos) = E2(pos);imagesc(x,y,E)
colormap(gray),colorbar
xlabel('x')
xlabel('y')
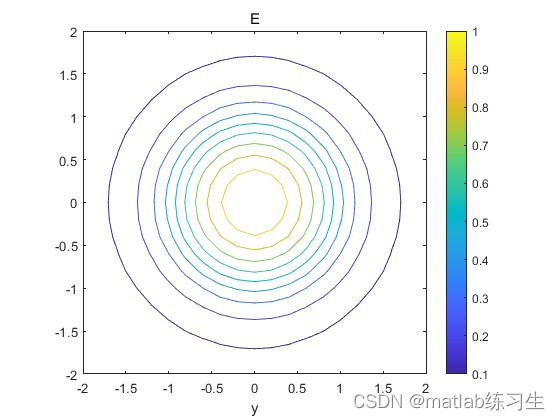
title('E')figure
[C, h]=contour(x,y,E);
colorbar;
axis equal
xlabel('x')
xlabel('y')
title('E')figure
[px,py] = gradient(E)
contour(X,Y,E)
hold on
quiver(X,Y,px,py)
hold off
axis equal
meshgrid函数产生网格,可以用一下代码来观察:
x = 1:3;
y = 1:5;
[X,Y] = meshgrid(x,y)对应的输出结果如下:
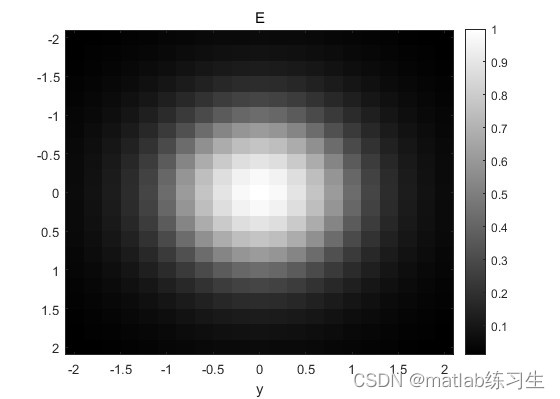
这里我们绘制的灰度图,可以将对应的语句注释掉:
%colormap(gray)转换为彩色图形
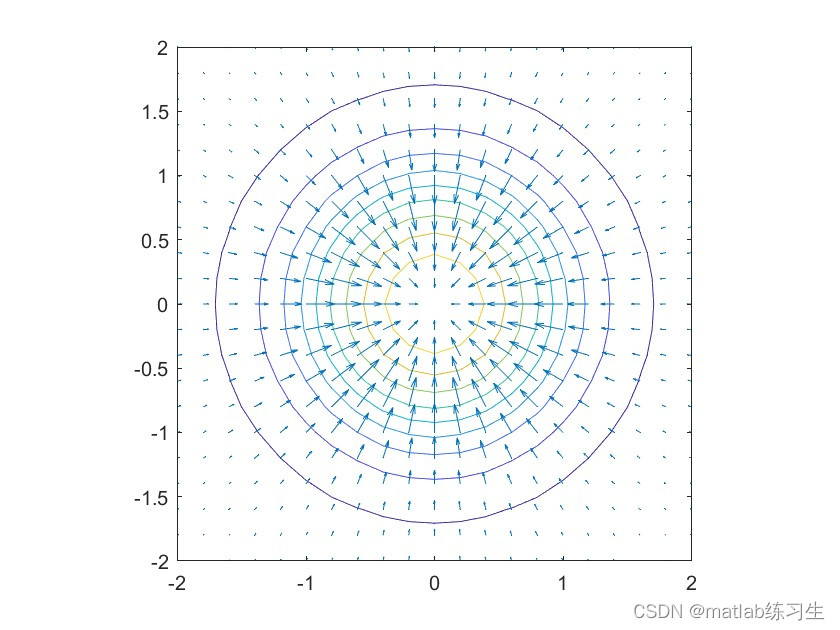
从图中可以看出,纤芯部分的光强最强,整体成圆对称分布;
图三的箭头很好的说明了这一点;
注意这里的箭头不代表光强降低,反而代表光强增加
这是由箭头绘制时,梯度函数gradient的结果决定的
如果想要得到通常意义上的梯度图(沿着光强降低的方向绘制箭头),可以使用:
quiver(X,Y,-px,-py)
结果:

可以看出,同一位置的数字两两对应组成了整个矩阵的位置坐标
find函数找出坐标R比1大的数值,返回对应的数组序号。
本身它的输入参数应当是一个数组,返回数组中每个非零元素的线性索引向量
不过,我们通过R>=1得到一个数组,这相当于进行了数组的逻辑运算,我们可以用下列代码来观察:
R >= 1注意命令行中的输出矩阵,由0和1组成,可以代表该位置的R是否大于1
imagesc函数用于绘制图像,生成像素网络
具体可以参考《MATLAB基础操作》专栏的二维绘图和三维绘图介绍
这个函数在每一个位置(矩阵)输出一个颜色,颜色的选择根据矩阵在该位置的数值决定。
contour函数绘制等高线图,这里没有打开等高线的标签,可以通过一下语句打开
set(h,'ShowText','on','TextStep',get(h,'LevelStep'))在每一条等高线上增加“高度”。
输出结果如下:
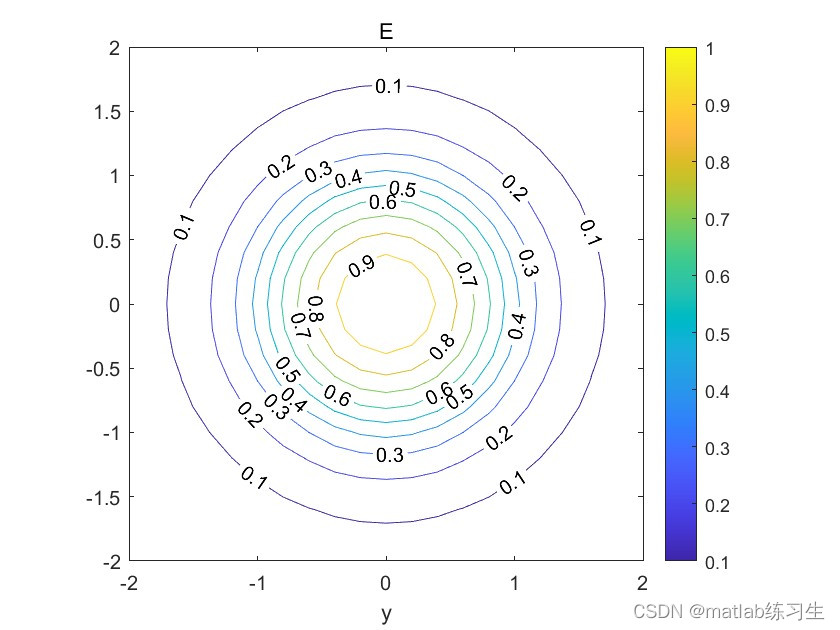
gradient函数 F 的一维数值梯度。输出 FX 对应于 ∂F/∂x,即 x(水平)方向上的差分。点之间的间距假定为 1。
同理Fy对应于y方向上的差分
quiver函数在由 X 和 Y 指定的笛卡尔坐标上绘制具有定向分量 U 和 V 的箭头。例如,第一个箭头源于点 X(1) 和 Y(1),按 U(1) 水平延伸,按 V(1) 垂直延伸。默认情况下,quiver 函数缩放箭头长度,使其不重叠。
来源《MATLAB高等光学仿真——光波导、激光》