SAP 的 ALV 全称是 SAP List Viewer，是 SAP 用于显示行列表格化数据的主要方式，从 SAP 推出的技术来看，大体有如下几种

• 函数生成 ALV，调用 REUSE_ALV*相关的函数
• ALV Grid 控件框架：SAP 提供 cl_gui_alv_grid 类，以面向对象的方式实现
• SALV: SAP 另外一种面向对象的实现，与 ALV Grid 比较起来，简化了开发的复杂程度。但不支持 ALV 编辑

Function Module based ALV 是较早出现的开发技术。使用 ALV 显示数据，首先需要知道输出什么数据(内表类型的数据结构)，还需要知道输出数据的数据结构（比如第一列显示什么，第二列显示什么，如何对齐，表头是什么，宽度多少，等等）。SAP 将这个数据结构称为 Field catalog。我们用一个简单的例子来讲解 ALV 的基本用法，假设要选取 spfli 表的部分字段在 ALV 中输出。

首先，定义要输出的字段：

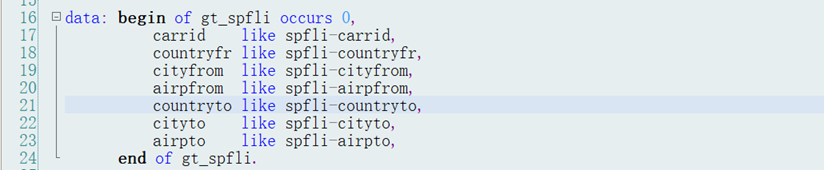
然后，从数据库表中获取数据：

根据 gt_spfli 的结构，定义 field catalog，并且调用 REUSE_ALV_GRID_DISPLAY 显示数据：

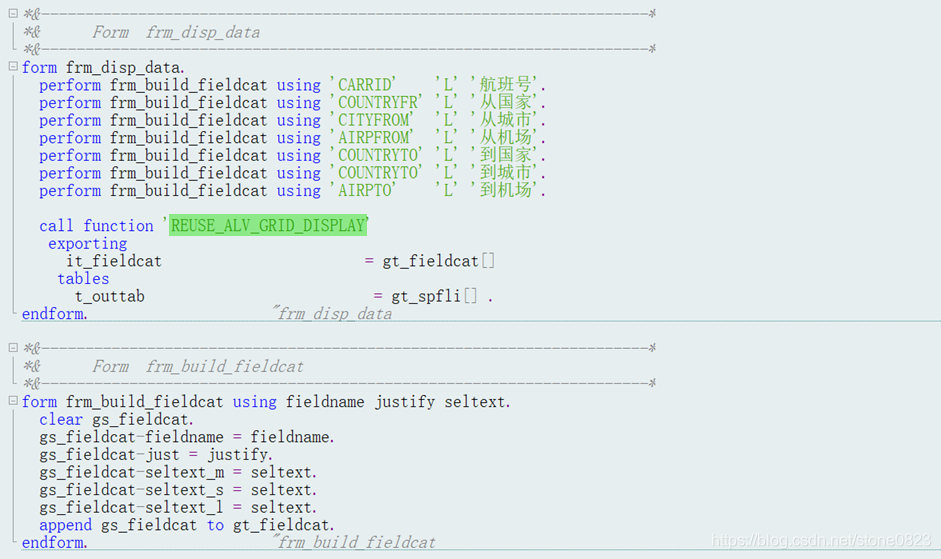
程序运行界面：

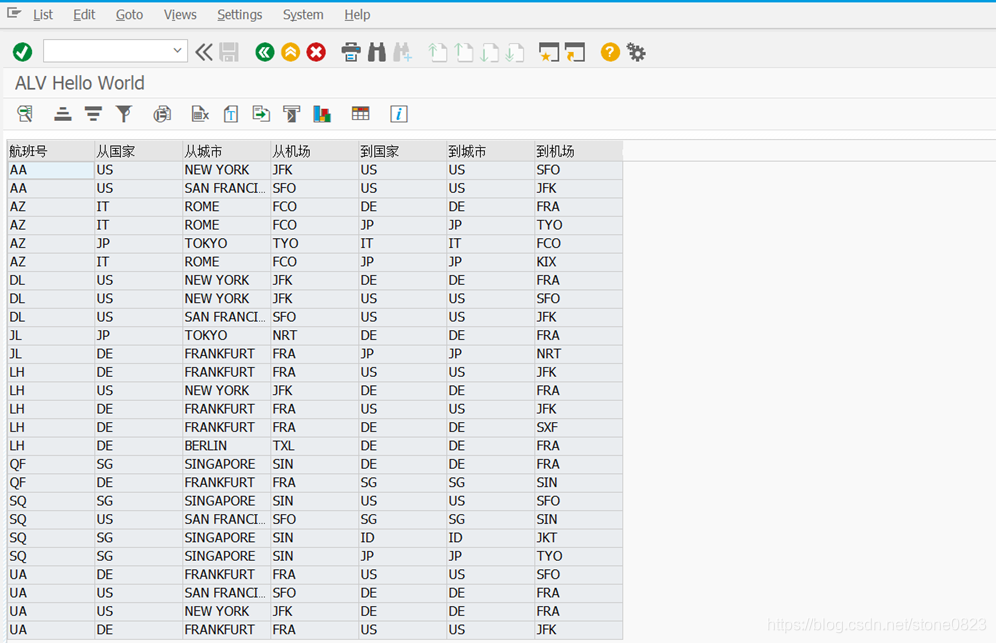
ALV 显示具有行列格式的数据，大致如此。我们发现，程序中相当多的代码都是用于处理 field catalog (属于 slis_t_fieldcat_alv 类型)，我们在调用 reuse_alv_grid_display 之前的代码打一个断点，观察 field catalog 的结构：

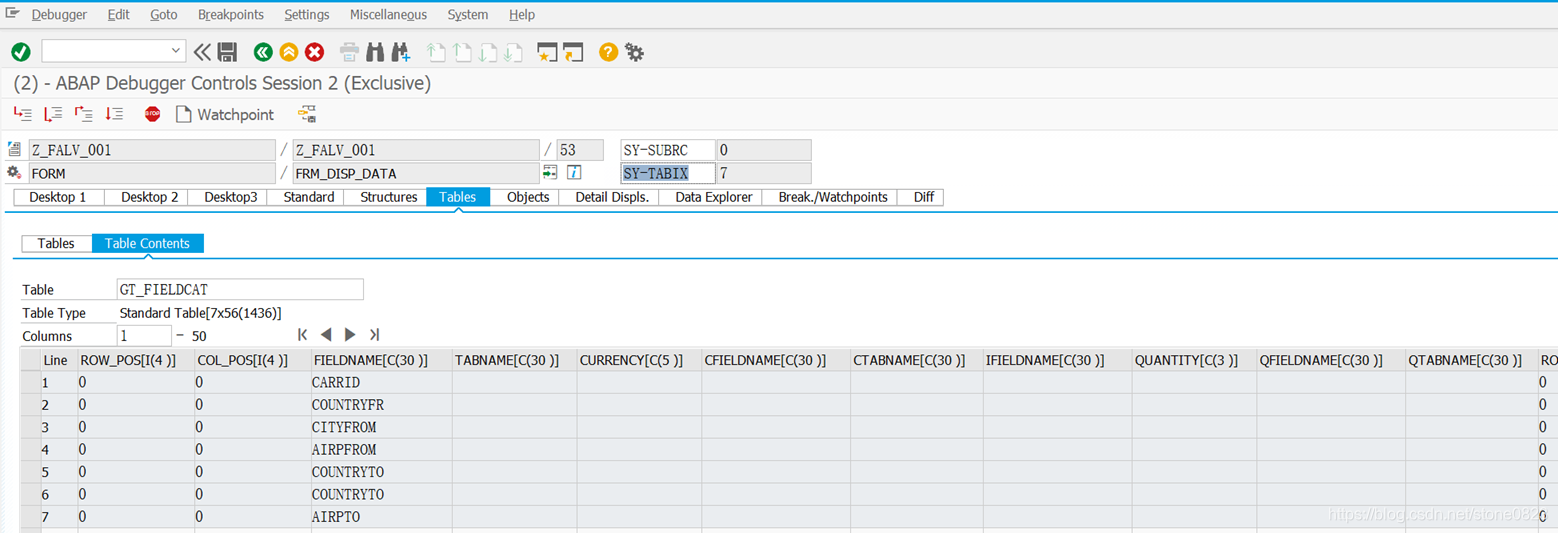
刚才的程序，很多代码都是用于加工 field catalog，如果是从数据库表中显示数据，能不能自动创建 field catalog 呢? 答案是可以的，我提供一种通用的方法。首先编写代码实现从 DDIC 或者内表中获取所有字段：

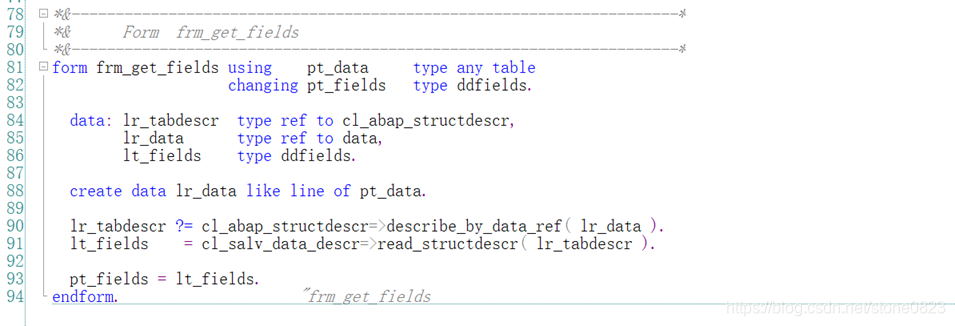
根据获取的字段填充 field catalog:

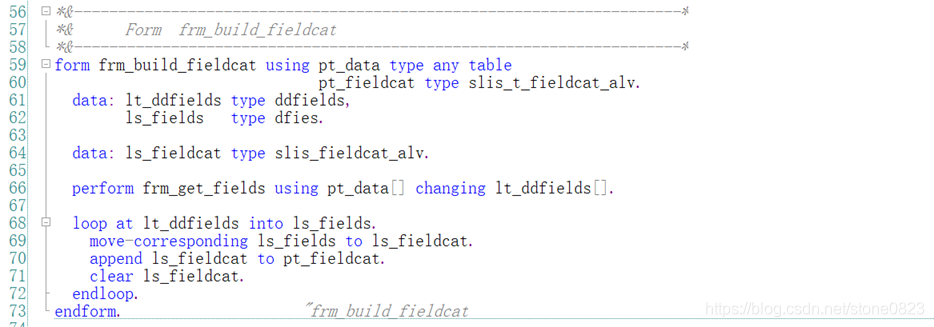
然后在程序中就可以调用 frm_build_fieldcat 来填充 field catalog:

代码量大大降低，该代码具备通用性。

源码

FALV/01-Hello World