二叉树的删除

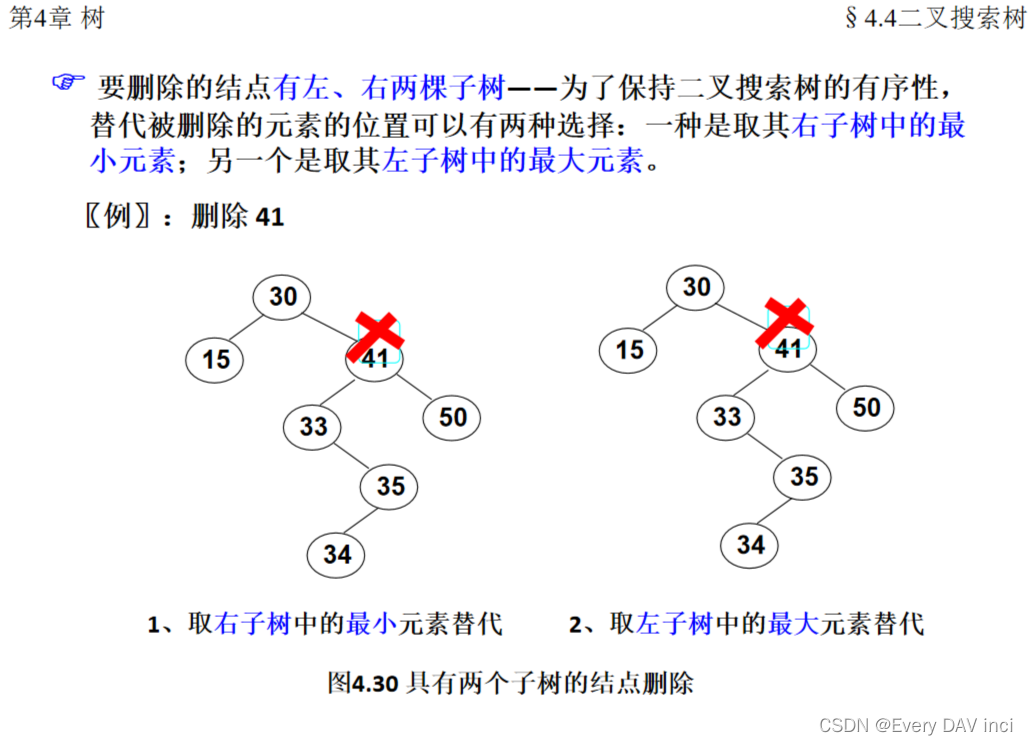最值节点一定是叶节点，没有子树，所以在移动最值节点后删除的时候不用考虑最值节点下的节点移动问题。

完全二叉树和完美二叉树的区别：

完美二叉树：一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树

​ 深度：树的根节点到该节点的边的个数，树的深度等于树中该节点的最大层次

​ 层次：根节点为第0层，根的孩子为第1层

**完全二叉树：**每个节点都有左右节点

​ 完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

参考文档

Three Tranverse Ways:

PreOrderTranverse

根节点->左节点->右节点 (*)

如果左节点或者右节点也是一棵树, 则以递归的方式继续(*)步骤

InOrderTranverse

左节点->根节点->右节点 (*)

如果左节点或者右节点也是一棵树, 则以递归的方式继续(*)步骤

二叉排序树的中序遍历一定是有序递增的数列

PostOrderTranverse

左节点->右节点->根节点 (*)

如果左节点或者右节点也是一棵树, 则以递归的方式继续(*)步骤

参考文档

AVL树深度为n时的最少节点数：

要注意题目中定义空树所在深度

一般我们默认根节点所在的深度为0

AVL树深度为n时的最少节点数遵循斐波那契数列

即最少节点数随树深度变化的递推公式为 :

F(n) = F(n-1) + F(n-2) + 1 ( n>=3 )

举例:

根节点所在层数为第0层, 最少节点数为1

根节点的子节点所在层数为第1层, 最少节点数为2

则第2层的最少节点数即为: 1 + 2 + 1 ,即4

例题:

空树深度定义为0, 即根节点深度为1, 那么此时F(1) = 1 F(2) = 2 , 而非F(0) = 1 F(1) = 2

此时要计算F(5)

采用递归的方式

F(3) = F(1) + F(2) + 1 = 1 + 2 + 1 = 4

F(4) = F(2) + F(3) + 1 = 2 + 4 + 1 = 7

F(5) = F(3) + F(4) + 1 = 4 + 7 + 1 = 12

已知节点数判断AVL树的最大深度

F(n)所求的皆为深度为n时的最少节点数, 如果小于该节点数, 则无法有第n层

同样需要注意题目中所给出的关于空树的深度说明

举例

一般来说, 根节点所在深度为0

F(0) = 1, 即如果树的深度为0, 那么树中至少有1个节点

F(1) = 2, 即如果树的深度为1, 那么树中至少有2个节点

F(3) = F(0) + F(1) + 1 = 4, 即如果树的深度为2, 那么树中至少有4个节点

…

接下来按照最少节点数随树深度的递推公式依次计算即可
例题:

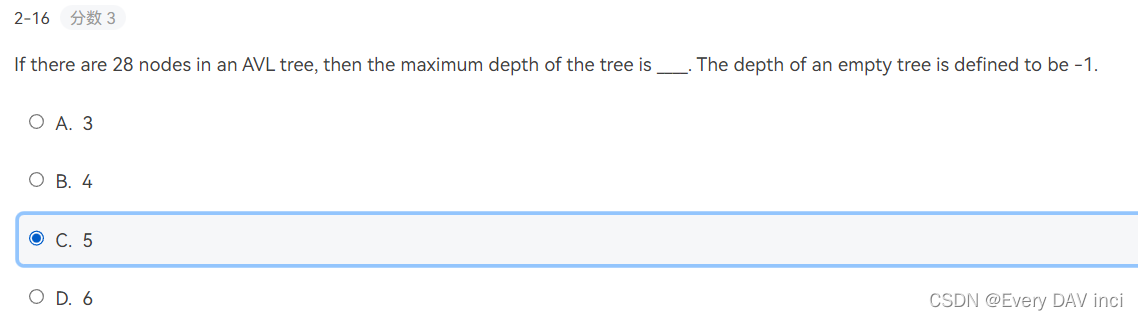
题中已明确说明空树的深度为-1, 即根节点的深度为0

即:

F(0) = 1

F(1) = 2

F(2) = 4

F(3) = 7

F(4) = 12

F(5) = 20

F(6) = 33 ----> 即如果树的深度要为6, 那么该树拥有的最少节点应为33

而题目中所给树的节点数为28, 即无法有第六层, 即树的深度只能为5

AVL的旋转

从旋转的个数对AVL的旋转进行分类：

单旋转：

​ 单左旋转

​ 单右旋转

双旋转：

​ 左左旋转

​ 右右旋转

​ 左右旋转

​ 右左旋转

双旋转中的分类有些笼统，未对左旋转和右旋转同时出现的情况有单独的归类

从旋转的形状对AVL的旋转进行分类：

单旋转 ：单左旋转 单右旋转

一字形旋转：左左旋转 右右旋转

之字形旋转：左右旋转 右左旋转

单旋转即按照方向直接旋转即可

一字形旋转就是按照指定方向进行两次单旋转

之字形旋转也是单旋转的累加，按照指定方向先后进行

在旋转过程中要严格遵守两个性质：

1、二叉搜索树的排序性质：一个节点大于其左节点，小于其右节点

2、平衡二叉树的平衡性质：一个节点的左右两颗子树的高度差不超过1

这两种性质都满足递归性

例题1：

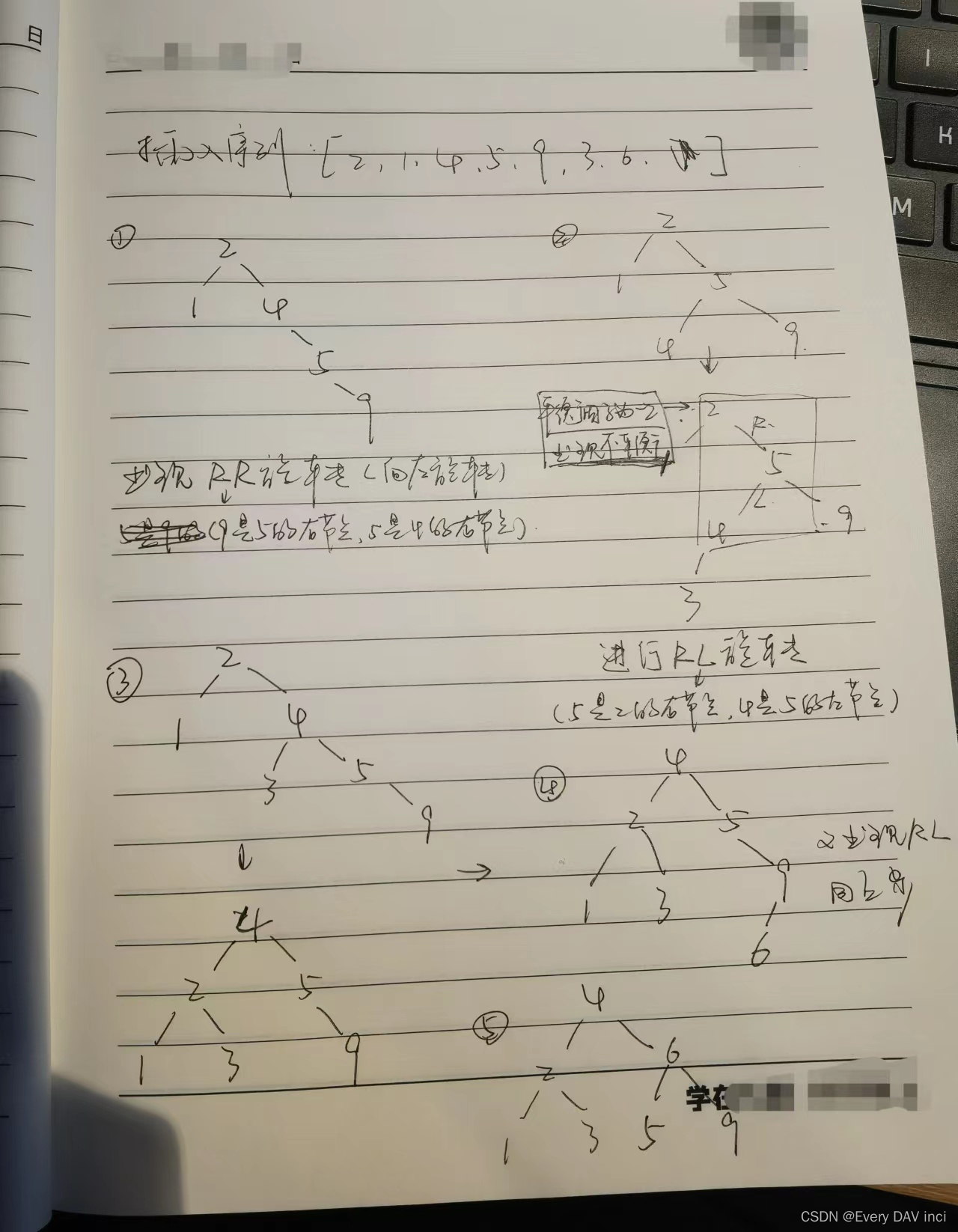
例题2：

SplayTree（伸展树）

伸展树即在对一个节点进行无论什么操作（插入，查询）后都将该节点移动到根节点的位置

伸展树的移动同样是利用旋转

伸展树也是二叉搜索树，树的结构同样遵循二叉搜索树的排序性，即一个节点大于其左节点，小于其右节点

伸展树的旋转方式：

zig -> 单旋转

zig-zig -> 一字形旋转

zig-zag -> 之字形旋转

AVL树是找不平衡节点, 是自上而下的, 要将整棵树调整为平衡状态

Splay树是找操作节点, 是自下而上的, 要将操作节点移动到根节点

例题:

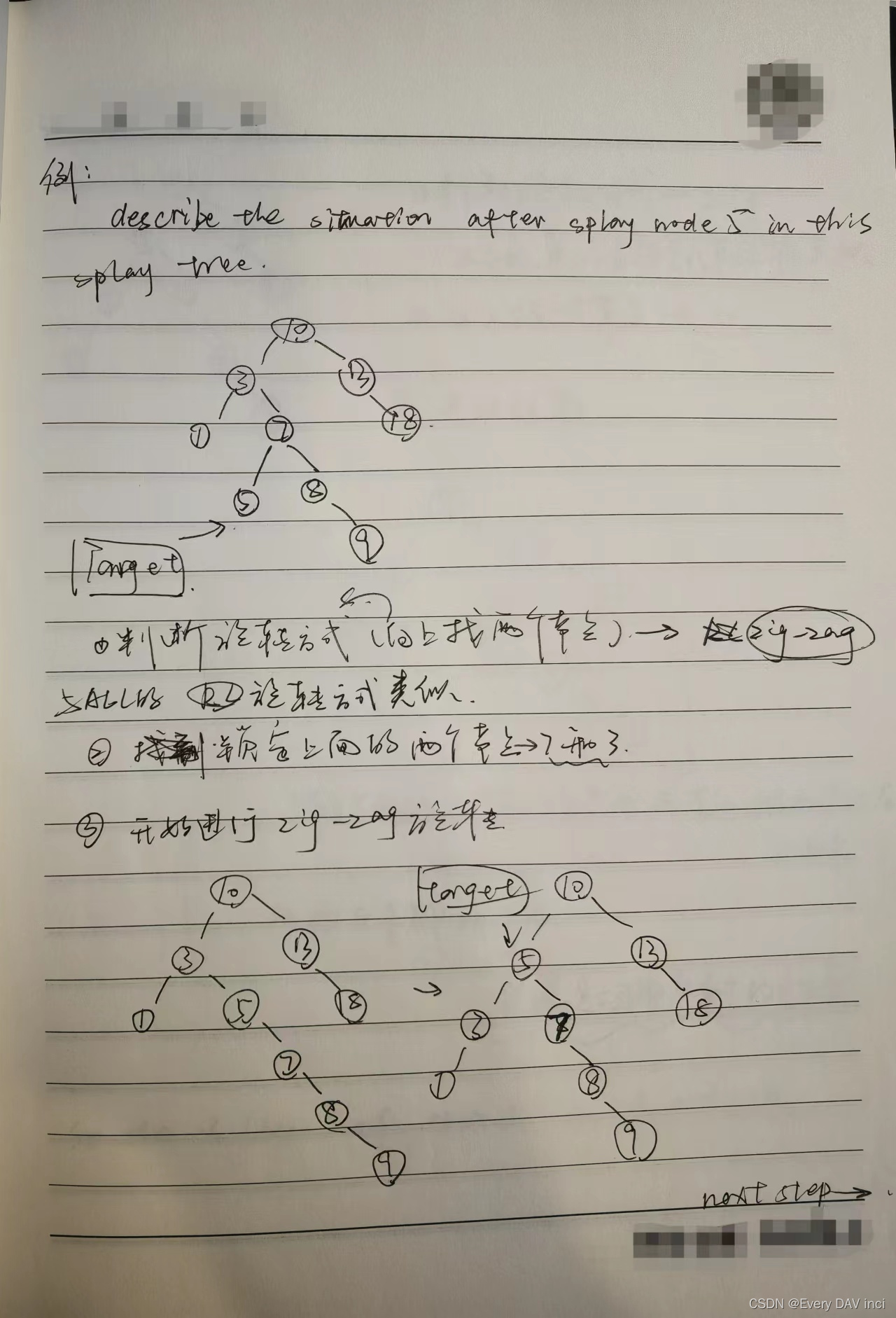
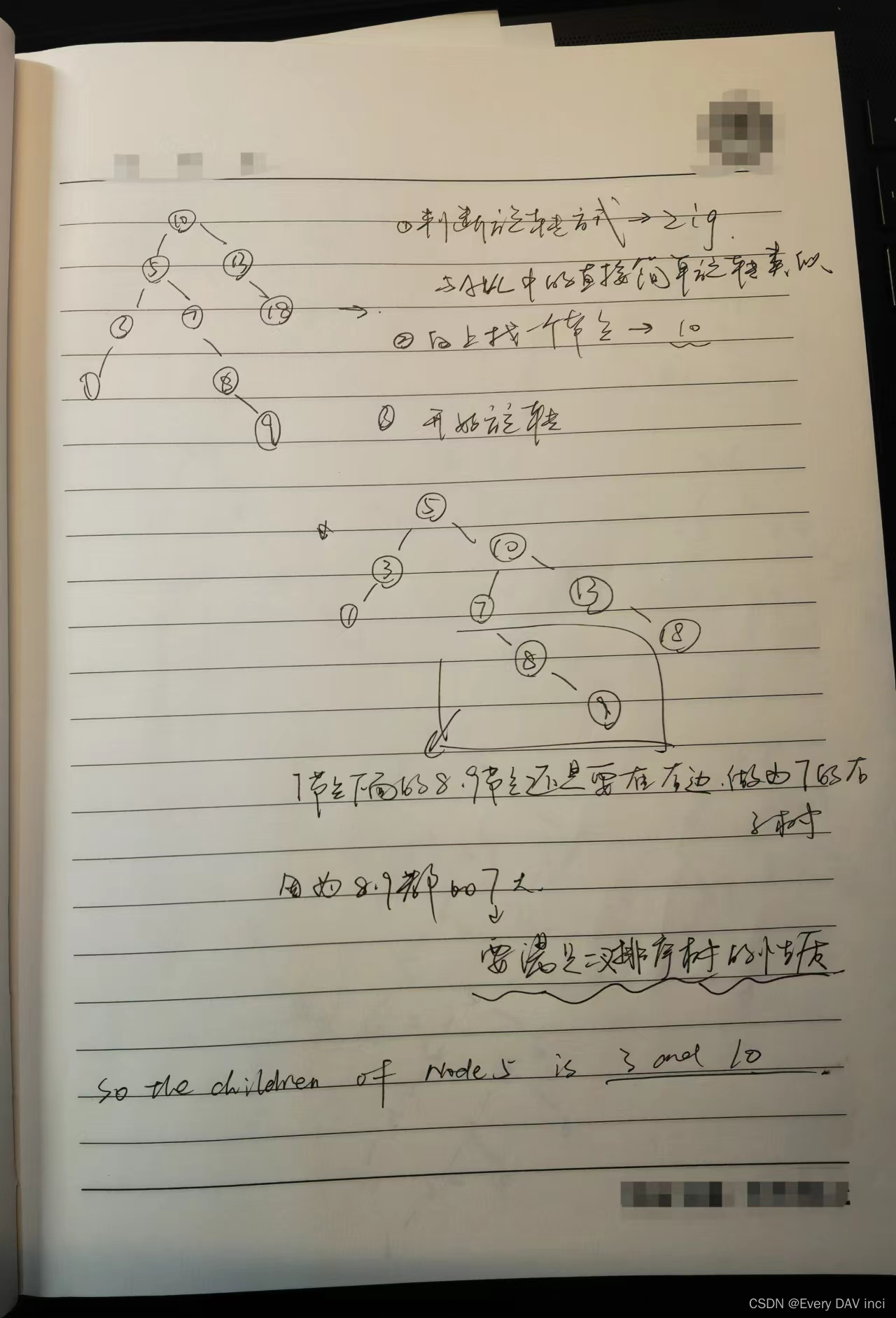
二叉树的插入操作-程序实现

#include <stdio.h>
#include <stdlib.h>typedef struct AVLNode *PtrToAVLNode; //struct pointer
struct AVLNode{int Key;PtrToAVLNode Left; // define new Node using structPtrToAVLNode Right;int Height;
};
typedef PtrToAVLNode AVLTree;AVLTree Insert ( AVLTree T, int Key );void PostOrderPrint( AVLTree T ); /* details omitted */
void InOrderPrint( AVLTree T );   /* details omitted */int Max(int a, int b){return a>b?a:b;
}/* The height is used to compute balance factor and determine which rotation will be used in the endNode A of `AVLTree A` needs to refer to the specific node in the insert methodThe change in height happens on every operationSo in this method,you can only see that the value property of the node itselt has changed
*/
int GetHeight(AVLTree A){if(A==NULL)return 0;return A->Height;
}AVLTree SingleLeftRotation(AVLTree A){AVLTree B=A->Right;A->Right=B->Left;B->Left=A;// renew the height of the node to calculate the value of balance factor in insert method// the following three rotation ways are the sameA->Height = Max(GetHeight(A->Left), GetHeight(A->Right)) + 1;B->Height = Max(GetHeight(B->Right), A->Height) + 1;return B;
}AVLTree SingleRightRotation(AVLTree A){AVLTree B=A->Left;A->Left=B->Right;B->Right=A;A->Height=Max(GetHeight(A->Left), GetHeight(A->Right))+1;B->Height=Max(GetHeight(B->Left),A->Height)+1;return B;
}// Double rotation equals single rotation plus single 
AVLTree DoubleLeftRightRotation(AVLTree A){A->Right = SingleRightRotation(A->Right);return SingleLeftRotation(A);
}AVLTree DoubleRightLeftRotation(AVLTree A){A->Left = SingleLeftRotation(A->Left);return SingleRightRotation(A);
}AVLTree Insert(AVLTree T,int X){if(!T){T=(AVLTree)malloc(sizeof(struct AVLNode));T->Key=X;T->Height=1;T->Left=T->Right=NULL;}else if(X<T->Key){ //插入左子树T->Left=Insert(T->Left, X);if(GetHeight(T->Left)-GetHeight(T->Right)==2){if (X<T->Left->Key) {T=SingleRightRotation(T);}elseT=DoubleRightLeftRotation(T);}}else if(X>T->Key){T->Right=Insert(T->Right, X);if(GetHeight(T->Left)-GetHeight(T->Right)==-2){if (X>T->Right->Key)T=SingleLeftRotation(T);elseT=DoubleLeftRightRotation(T);}}T->Height=Max(GetHeight(T->Left), GetHeight(T->Right))+1;return T;
}int main()
{int N, Key, i;AVLTree T = NULL;scanf("%d", &N);for ( i=0; i<N; i++ ) {scanf("%d", &Key);T = Insert( T, Key );}PostOrderPrint( T );InOrderPrint( T );return 0;
}