一.题目分析
题目要求:
1.求N个数的最大公约数和最小公倍数
2.已知a0,a1,b0,b1,设某未知正整数x满足:
(1)x和a0的最大公约数为a1;
(2)x和b0的最小公倍数为b1;
求出满足该规则x的个数
题目思路:
(1)求N个数的最大公约数和最小公倍数
1.先求出N个数中的最大值和最小值
2.利用穷举法求最大公约数和最小公倍数
3.利用循环求出任意一个数被N个数整除的次数以及任意一个数把N个数整除的次数
4.如果求出的次数与N值相等,那么对应的这个被整除的数就是最大公约数,整除的数就是最小公倍数
(2)求出满足的x的个数
1.从1开始循环,到一个比较大数结束
2.如果存在一个数与a0的最大公约数为a1,记下这个数为X
3,接着去验证这个x与b0的最小公倍数是否等于b1,如果等于,则这个x是满足Hankson规则,记录个数的值加
二.算法构造
1.求N个数最大公约数和最小公倍数的流程图

2.求出满足条件x的个数

三.算法实现
程序源代码:
package harkson;
import java.util.Scanner;//导包
public class Harkson {
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);//创建键盘录入对象
System.out.println(“求N个数的最大公约数和最小公倍数”);
System.out.println(“请输入N的值”);
int N=sc.nextInt();//用来存储需要求最大公约数的个数
System.out.println(“请输入N个数据:”);
int data[]=new int[N];
for(int i=0;i<N;i++)
{
data[i]=sc.nextInt();
}
gcdAndLcm(data);//求最大公约数和最小公倍数的方法
System.out.println("--------------");
System.out.println(“请输入数据的组数::”);
int M=sc.nextInt();
//定义一个二维数组来存储数据,M代表数据的组数,4分别代表a0,a1,b0,b1;
int[][] array=new int[M][4];
for(int j=0;j<M;j++)
{
System.out.println(“请输入第”+(j+1)+“组数据”);
array[j][0]=sc.nextInt();//键盘录入
array[j][1]=sc.nextInt();
array[j][2]=sc.nextInt();
array[j][3]=sc.nextInt();
}
//已知x,a0的最大公约数为a1,x,b0的最小公倍数为b1;
//所以a0>=a1;b1>=b0;,
//所以利用dataValidation方法对输入数据的规范性进行验证
if(dataValidation(array,M)==1)
{
harkson(array,M);//求出满足harksO规定的x值
}
}//判断输入数据的规范性
public static int dataValidation(int array[][],int N)
{int leap=1;//判断循环是否提前结束的变量for(int j=0;j<N;j++){if(array[j][2]>array[j][3])//判断a0>=a1;b1>=b0关系式是否成立if(array[j][1]>array[j][0]){System.out.println("输入数据不符合规则");//如果不成立,则输入数据不符合规则leap=0;break;}}return leap;//利用返回值来判断harskon方法是否继续进行
}//利用harkson提出的方法,求出满足条件的x的个数
public static void harkson(int array[][],int N)
{for(int j=0;j<N;j++)//利用循环,求出每一组数据x的个数{int x=0;int ans=0;for(int i=1;i<10000;i++){if(gcd(i,array[j][0])==array[j][1]) {//gcd方法为求俩个数的最大公约数x=i;//如果x和a0的最大公约数是a1,满足第一条规则,再用这个x来验证第二条规则if(lcm(x,array[j][2])==array[j][3]) {//lcm方法为求俩个数的最小公倍数ans++;//如果x和b0的最小公倍数是b1,满足第二条规则,记录x个数的ans变量++System.out.println("x="+x);}}}System.out.println("满足x个个数为:"+ans);}}//求出俩个数的最大公约数
public static int gcd(int a,int b)
{if(a%b==0)return b;elsereturn gcd(b,a%b);//递归
}//求出俩个数的最小公倍数
public static int lcm(int a,int b)
{return a*b/gcd(a,b);//a*b除以a和b的最大公约数
}//求出N个数的最大公约数和最小公倍数
public static void gcdAndLcm(int data[])
{int max=data[0],min=data[0];for(int j=1;j<data.length;j++)//求出N个数的最大值{if(data[j]>max)max=data[j];}for(int j=1;j<data.length;j++)//求出N个数的最小值{if(data[j]<min)min=data[j];}int gcd=0;//最大公约数int m;for(int j=min;j>0;j--)//穷举法{m=0;//记录可以被j整除的数的个数for(int k=0;k<data.length;k++)if(data[k]%j==0){m++;}if(m==data.length)//可以整除j的个数与总数相等,则证明每一个数都整除j,则j为最大公约数{gcd=j;System.out.println("最大公约数为:"+gcd);break;}}//求N个数的最小公倍数的方法与求最大公约数的方法一样,使用穷举法int lcm=0;//最大公倍数for(int l=max;;l++){m=0;for(int k=0;k<data.length;k++)if(l%data[k]==0){m++;//记录能整除的个数}if(m==data.length){lcm=l;System.out.println("最大公倍数为:"+lcm);break;}}
}
}
四.调试、测试、及运行结果
调试:
一开始由于没有考虑到静态变量的关系,直接给max和min变量的初值设置成0,所以在求最大公约数的那个循环里,直接跳出了循环,没有执行这个循环

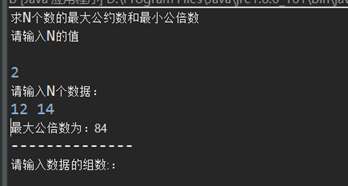
最后将max和min的初值设置成输入N数中第一个数值,就避免了该错误。
测试:
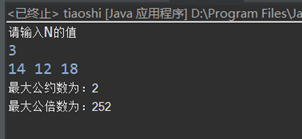
测试求N个数的最大公约数和最小公倍数


结果:
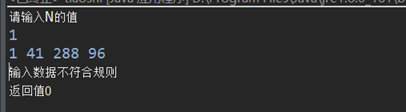
测试输入数据的正确性

结果:
测试求满足x的条件的个数


结果:
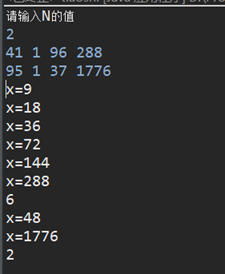
运行结果:

五。经验归纳
1.在写程序的时候,尽可能将一些比较长的代码放到一个方法中,使用的时候进行调用,这样所写的程序看起来不会太过繁琐。
2.写完程序以后,可以在网上看看其他人所写的程序。对比一下自己与别人的区别,总结一下各自代码的优缺点。
3.写完程序以后,及时的对一些代码进行注释,方便自己和别人理解。