题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=6222

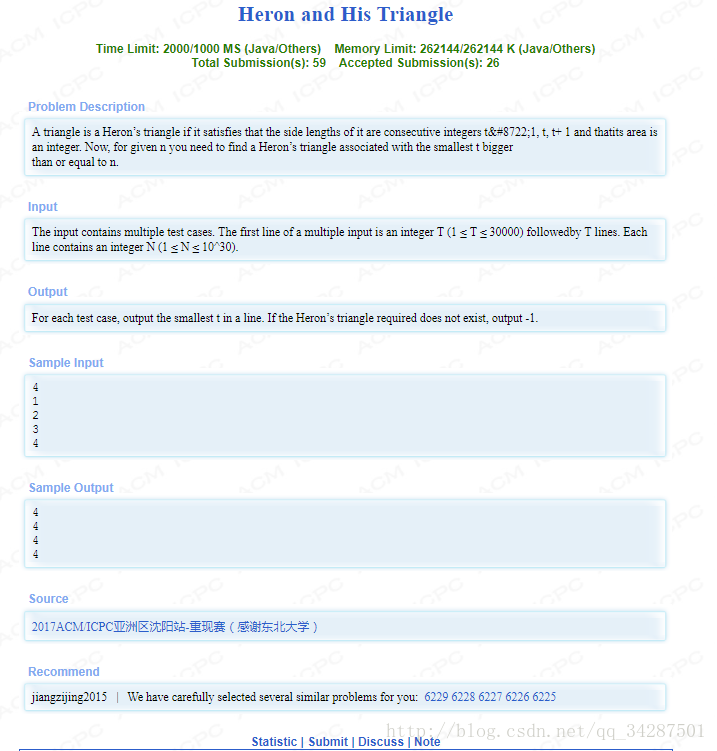
题目大意:

寻找大于n的最小数t

使得t-1，t，t+1这三个数构成的三角形为整数

n<10^30

思路：

看到n这么大，显然是瞎jiba找规律然后打表？

1.首先打表，打出所有的满足条件的t；

2.然后我们美滋滋的发现了规律；

3.按得出的递推式构造出10^30以内所有满足条件的数t；

4.对于每个n，在t的表里面顺序查找即可；

打表代码：

利用海伦公式

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
using namespace std;int i,t,s,pd,delta;int main()
{for (t=1; t<=100000; t++){int delta=3*(t*t-4);int pd=floor(sqrt(delta));if (pd*pd!=delta) continue;delta=pd;if ((t*delta)%4!=0) continue;s=(t/4)*delta;if (s==0) continue; cout<<t<<' '<<s<<endl;}
}

打表后看前面几个数（t和面积）

4 6
14 72
52 1170
194 16128
724 226974
2702 3159000
10084 44031786

然后发现 f[i]=4*f[i-1]+f[i-2]

主代码：

#include<cstdio>
#include<string>
#include<iostream>
#include<cstring>
using namespace std;int a[1000],b[1000],c[1000];
string st[1000];
char S[1000];
int T,i,la,lb,j,L;
string sta,stb;int main()
{scanf("%d\n",&T);st[1]="4";st[2]="14";for (i=3; i<=100; i++){sta=st[i-2];   stb=st[i-1];la=sta.size(); lb=stb.size();memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(c,0,sizeof(c));for (j=0; j<la; j++) a[la-j]=sta[j]-'0';for (j=0; j<lb; j++) b[lb-j]=stb[j]-'0';for (j=1; j<=lb; j++) b[j]*=4;for (j=1; j<=lb; j++) b[j+1]+=b[j]/10,b[j]=b[j]%10;while (b[lb+1]!=0) lb++;L=lb;for (j=1; j<=L; j++) c[j]=b[j]-a[j];for (j=1; j<=L; j++) if (c[j]<0) {  c[j]=c[j]+10; c[j+1]--; }while (c[L]==0) L--;string temp="";for (j=L; j>=1; j--) temp+='0'+c[j];st[i]=temp;}
//	利用公式做高精度运算，然后制表 for (i=1; i<=T; i++){gets(S);int p=1;string temp="";for (j=0; j<strlen(S); j++) temp+=S[j];bool have=0;for (j=1; j<=100; j++) if (st[j].size()>temp.size() || (st[j].size()==temp.size() && st[j]>=temp))  { have=1; break; }if (have==0) cout<<-1<<endl; else cout<<st[j]<<endl;	}
//   顺序查找即可 }