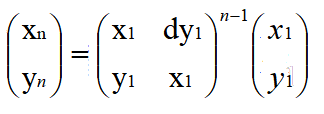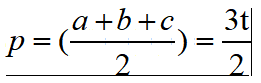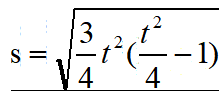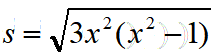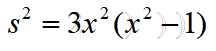背景介绍

佩尔方程，是一种不定二次方程。Pell方程，古希腊和印度的数学家对此类方程的研究做了最早的贡献，由费马首先进行了深入研究，拉格朗日给出了解决方案，但后此类方程来却被欧拉误记为佩尔提出，并写入他的著作中。后人多称佩尔方程。沿续至今。

内容简介

佩尔方程是一种不定二次方程。就是如下形式的方程
x² - dy² = 1;
1)，如果d为平方数，则方程变为了(x-√dy)(x+√dy) = 1,此时只有x = 1或-1，y=0，这两组特定解。
2)，当d不为平方数时，方程有无穷多组整数解。

求解最小整数解

已知x²-dy² = 1,
假设(x₁, y₁), (x₂, y₂)，满足上面的式子，带入后得到

$x_1^2$ - d * $y_1^2$ = 1
$x_2^2$ - d * $y_2^2$ = 1

将上面两个式子相乘后得到
$x_1^2$ * $x_2^2$ - d$x_1^2$$y_2^2$ -d$y_1^2$$x_2^2$ +d²$y_1^2$$y_2^2$ = 1

整理后得到
[(x₁x₂)² + (dy₁y₂)²] - d[(x₁y₂)² + (x₂y₁)²] = 1

对左边和右边同时加上 2dx₁y₁x₁y₂后变为了如下形式
(x₁x₂ + dy₁y₂)² - d(x₁y₂ + x₂y₁)² = 1

神奇的发现它还是一个佩尔方程这个时候
x = x₁x₂ + dy₁y₂
y = x₁y₂ + x₂y₁

所以也就得到了一个递推式
x_n = x_n-1x₁ + dy₁y_n-1
y_n = x₁y_n-1 + x_n-1y₁

进一步变换后就能变为了下面这个矩阵，所以再求某个特解的时候可以用矩阵快速幂

所以我们只要求得最小解后，就能求得所有的解。
求最小解有两种方法，连分数和暴力，我现在还没太看懂连分数，后期看懂再补。

#include <iostream>
#include <cmath>using namespace std;int main()
{int d;int y = 1, x = 0;cin >> d;while (1){x = sqrt(1+d*pow(y, 2));if (x*x - d*y*y == 1){break;}y++;}cout << x << " " << y << endl;return 0;
} 

hdu6222

接下来就到了例题了
题目地址：
http://acm.hdu.edu.cn/showproblem.php?pid=6222

题目大意：
一个三角形三边满足t-1, t, t+1，就称为什么什么的，现在他给你一个最小的n，让你找到大于等于这个n的t。

解题思路：

求三角形面积用海伦公式来求：

我们设a = t-1, b = t, c = t+1

所以

带入海伦公式后得到

令x = t/2，得到

对两边同时平方后得到

因为s为整数，所以我们能知道x²-1=3*y²，整理后正好是我们今天的佩尔方程。
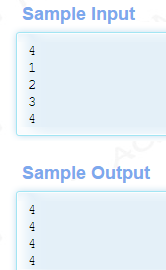
在看题目给的数据

当题目n等于1时，我们很轻松就得到了最小的t就是4，我们又知道x = t/2，所以最小的t对应最小的解，即x = 2，接着得出y=1 这便是上面佩尔方程的最小解。通过打表就能看到，当n在大于100的时候，就已经比10³⁰次方大了，所以可以把这些解存下来，也可以每次使用矩阵快速幂。
因为数据比较大，所以使用_ _int128来做题。

#include <iostream>using namespace std;typedef __int128 _int;_int num[105][2];void read(_int &x)
{char ch;int flag = 1;x = 0;while (ch = getchar()){if (ch == '-'){flag = -1;}else if (ch>='0' && ch<='9'){break;}}x = ch - '0';while ((ch = getchar())>='0' && ch <= '9'){x = x*10 + ch-'0';}x*=flag;
}void out(_int x)
{if (x<0){x = -x;putchar('-');}if (x>=10){out(x/10);}putchar(x%10+'0');
}int main()
{num[1][0] = 2, num[1][1] = 1;for (int i=2; i<=100; i++){num[i][0] = num[i-1][0]*num[1][0] + 3*num[i-1][1]*num[1][1];num[i][1] = num[i-1][1]*num[1][0] + num[1][1]*num[i-1][0];} int n;cin >> n;while (n--){_int temp = 0;read(temp);for (int i=1; i<=100; i++){if (num[i][0] * 2 >= temp){out(num[i][0]*2);puts("");break;}}}return 0;
}