引入

之前在b站上看到了一些介绍FFT的视频

《快速傅里叶变换(FFT)——有史以来最巧妙的算法？》
《这个算法改变了世界》

于是打算写一篇记录一下qwq（本博客中的截图基本上来源于第一个视频）

Fast Fourier Transform 是一种能在 $O (n l o g n)$ 的时间内将一个用系数表示的多项式转化成点值表示。

$P(x)=p_0+p_1x+p_2x^2+...+p_dx^d$

系数表示法： $p_0,p_1,p_2,...,p_d]$
点值表示法： ${(x_0,P(x_0),(x_1,P(x_1),...,(x_d,P(x_d))}$

(n+1个不同点可以确定一个n次的多项式：可以用矩阵列式求解）

当我们试图算两个多项式相乘的结果：

$A(x)=a_0+a_1x+...+a_dx^d$
$B(x)=b_0+b_1x+...+b_dx^d$

传统的做法需要 $O(n^2)$ ，而如果我们先求出若干个点的坐标（多少个点根据最后算出的会是几次多项式而定，比如A是三次多项式，B是五次多项式，算出来的C会是八次多项式，那么就需要找九个点），最后再根据这些点把多项式还原成系数表示，但是对于每个点，知道一个横坐标，需要(d+1)次计算才能知道这个点的纵坐标，总复杂度还是会达到 $O(n^2)$ ，达咩。

主要过程

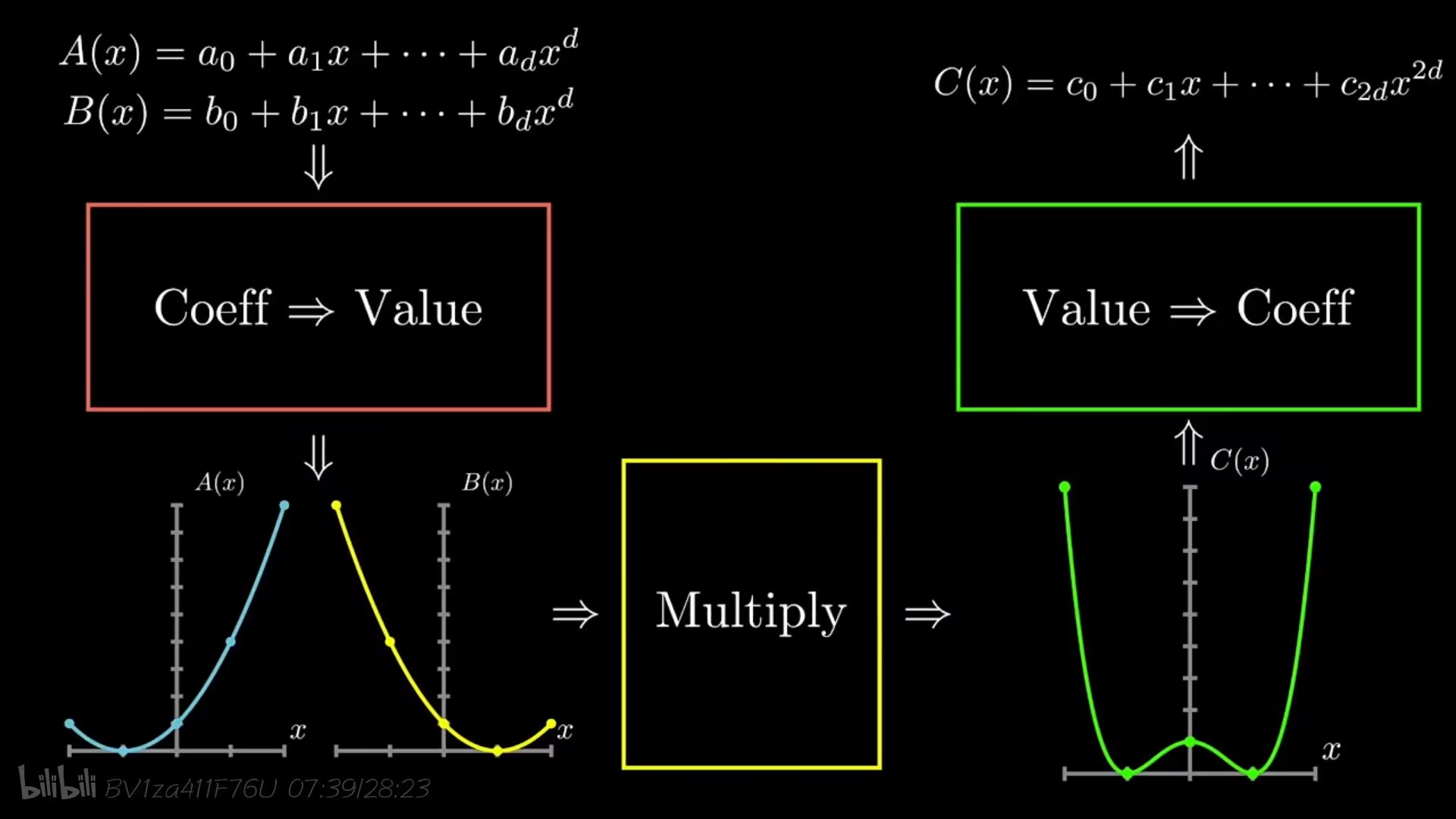
可不可以通过选取一些巧妙的点来减少我们的计算次数？

我们可以每次将多项式分成奇项和偶项，通过这样的划分可以便捷地算出横坐标互为相反数的一对点对的坐标，此时我们需要求出 $x^2$ 分别代入 $P_e(x^2)$ 和 $P_o(x^2)$ 算出来的值，原问题变成了两个子问题，每个子问题的次数是原问题的 $1/2$ 。我们想着能不能一直这么递归下去，直到分到底层（次数为1），再自底向上，层层归并求出答案？

实际上在递归步骤，我们假设了每个多项式我们都使用相反数对来求值，然而对两个子问题而言，每个求值点都是平方数，没办法继续了（悲.jpg）于是我们希望把新的求值点也弄成相反数对QAQ

（P.S.为了方便讨论，下文的n均为2的整数次幂，如果题目的n不是2的整数次幂，我们可以加一波操作~）

于是——复数大法好！

单位根

四次方根
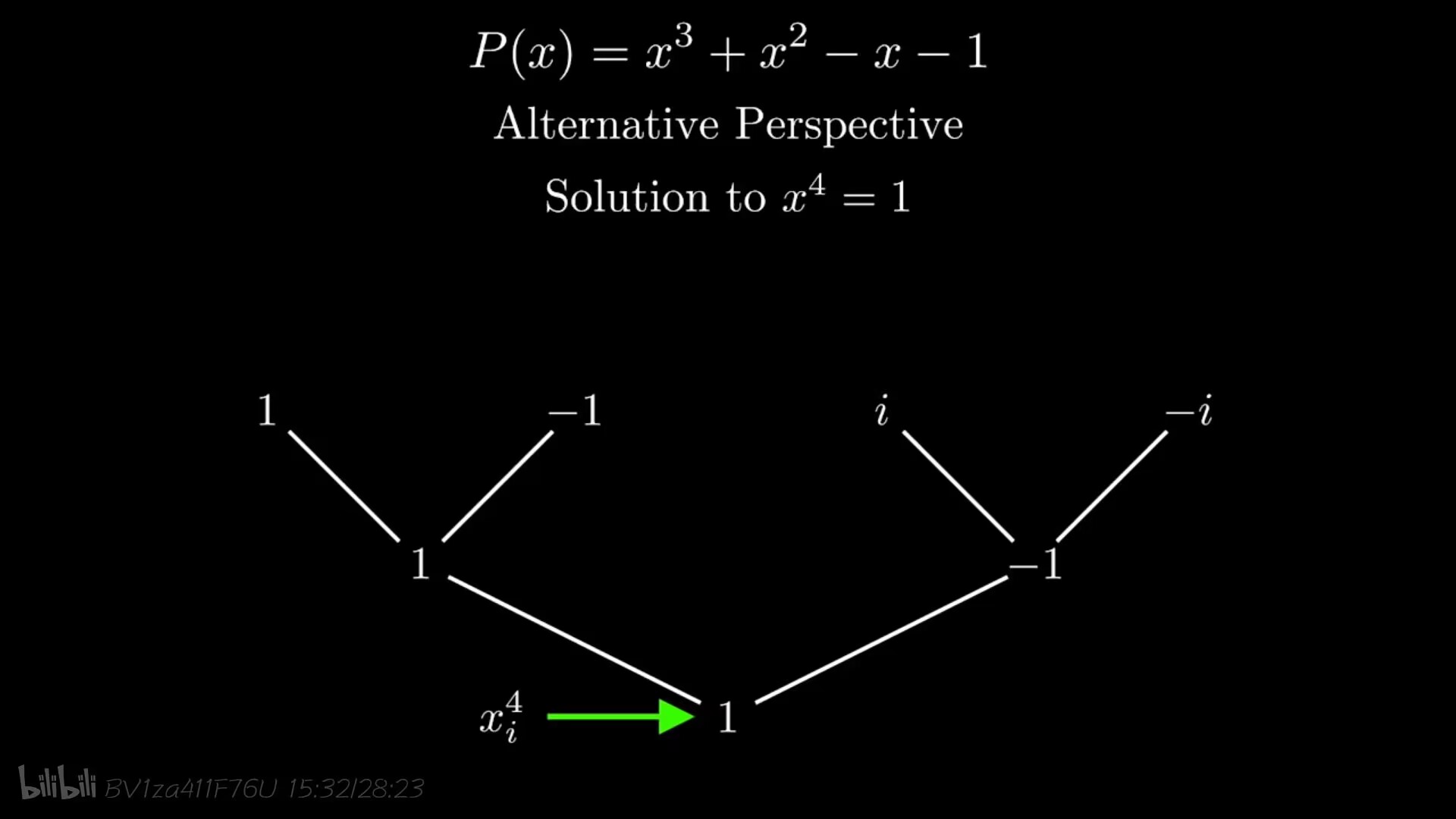
按照上面的逻辑推演，再向下递归一层我们需要两个相反点对，即要求出 $x^4=1$ 的四个解；
八次方根
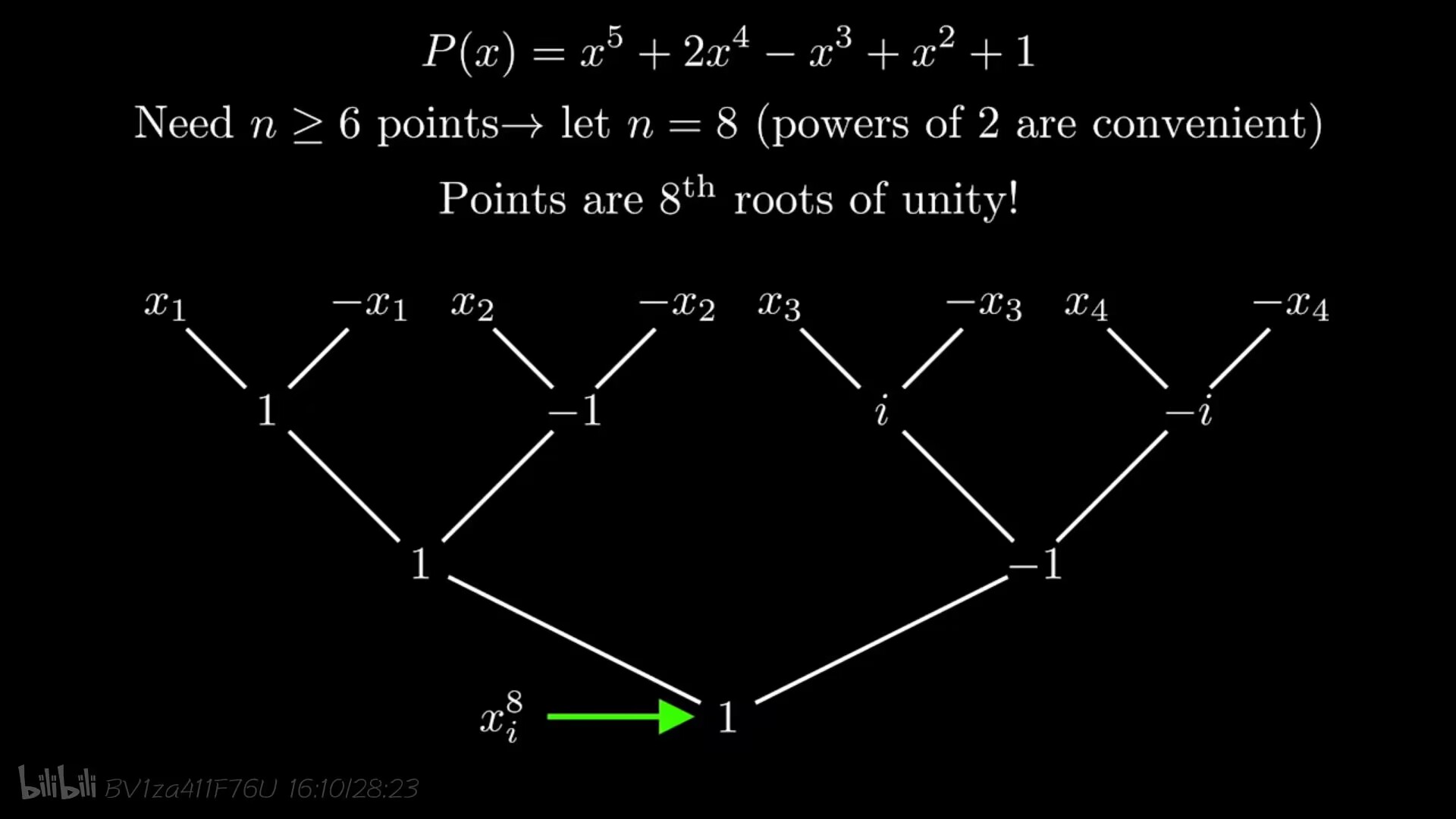
再向下递归一层我们需要四个相反点对，即要求出 $x^8=1$ 的八个解；
现在推广到d阶多项式，我们要先取n>d个点，（并且n等于2的整数次幂），我们为求解多项式乘积所选取的点就是1的n个n次方根。
单位根
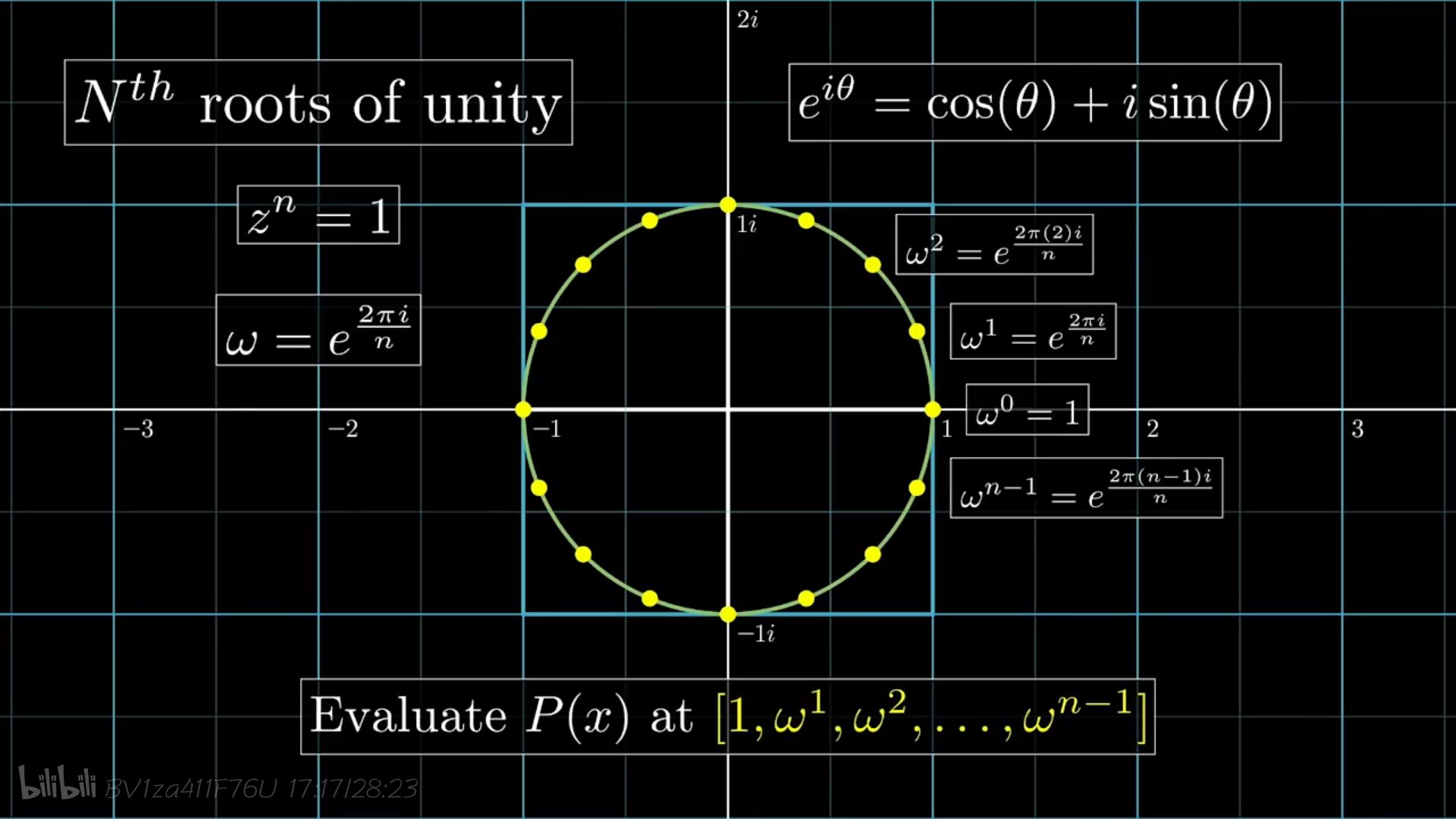
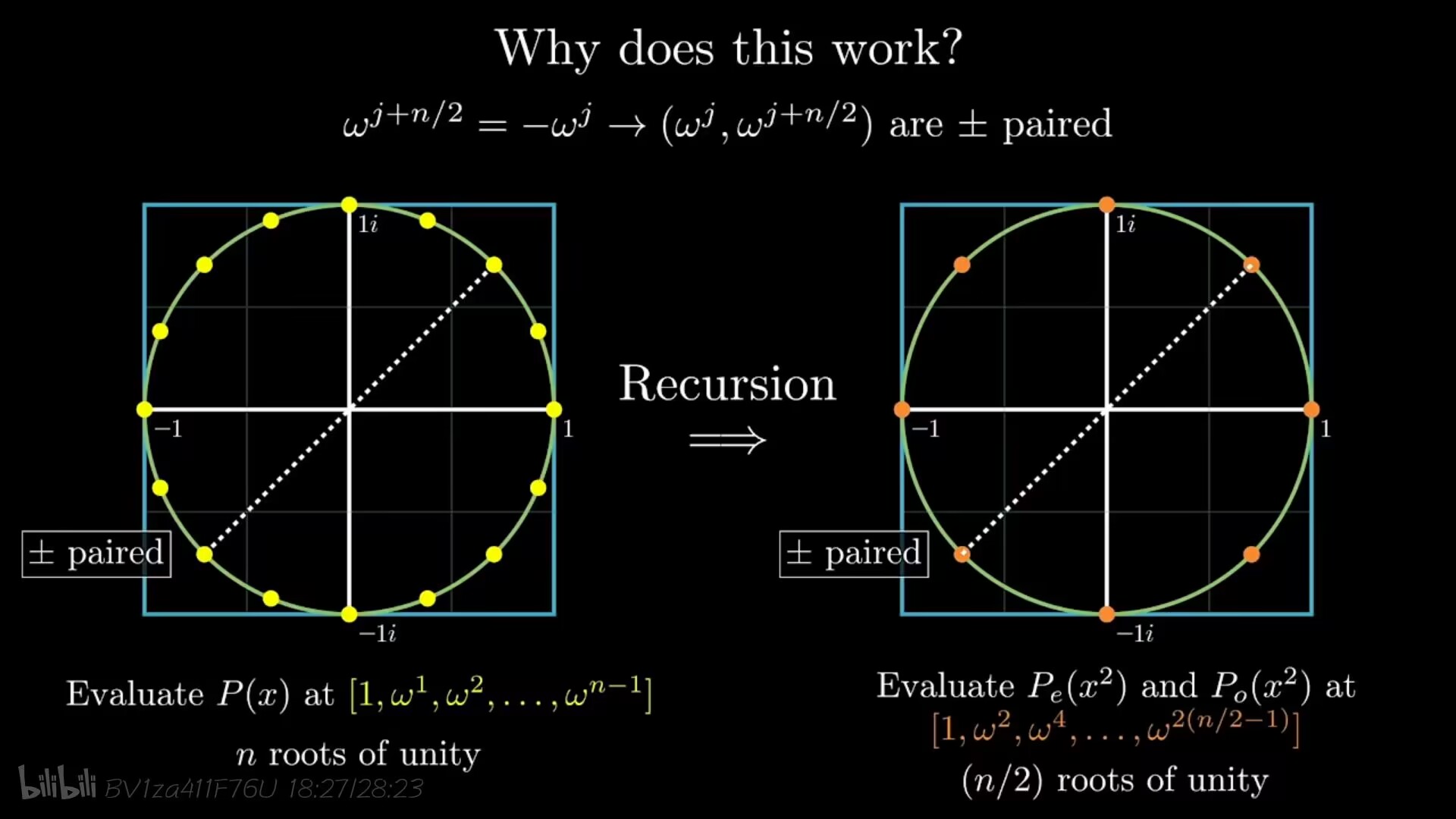
在这里插入图片描述

单位根的性质：

性质一： $ω2n2k=ωnkω^{2k}_{2n}=ω^{k}_n$

性质二： $ωnk+n/2=−ωnkω^{k+n/2}_n=−ω^k_n$ （对应的点关于原点对称）

快速傅里叶变换的数学证明

设 $A(x) = a_0 + a_1x + a_2x^2 +...+a_{n-1}x^{n-1}$ ，为求离散傅里叶变换，要把一个 $\omega_n^k$ 代入。

考虑将 $A (x)$ 的每一项按照下标的奇偶分成两部分：

$A(x) = (a_0 + a_2x^2 + ... + a_{n - 2}x^{n - 2}) + (a_1x + a_3x^3 + ... + a_{n-1}x^{n-1})$

设两个多项式：
$A1(x)=a0+a2x+...+an−2xn2−1A_1(x) = a_0 + a_2x + ... + a_{n - 2}x^{\frac{n}{2} - 1}$
$A2(x)=a1+a3x+...+an−1xn2−1A_2(x) = a_1 + a_3x + ... + a_{n - 1}x^{\frac{n}{2} - 1}$
则： $A(x) = A_1(x^2) + xA_2(x^2)$

假设 $\frac{n}{2}$ ，现要把 $\omega_n^k$ 代入，

$A(ωnk)=A1(ωn2k)+ωnkA2(ωn2k)=A1(ωn2k)+ωnkA2(ωn2k)\begin{align*} A(\omega_n^k) &= A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\ &= A_1(\omega_{\frac{n}{2}}^{k}) + \omega_n^kA_2(\omega_{\frac{n}{2}}^{k}) \end{align*}$
那么对于 $A(ωnk+n2)A(\omega_n^{k + \frac{n}{2}})$ :
$A(ωnk+n2)=A1(ωn2k+n)+ωnk+n2A2(ωn2k+n)=A1(ωn2k×ωnn)+ωnk+n2A2(ωn2k×ωnn)=A1(ωn2k)−ωnkA2(ωn2k)\begin{align*} A(\omega_n^{k + \frac{n}{2}}) &= A_1(\omega_n^{2k + n}) + \omega_n^{k + \frac{n}{2}}A_2(\omega_n^{2k + n}) \\ &= A_1(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) + \omega_n^{k + \frac{n}{2}} A_2(\omega_{\frac{n}{2}}^{k} \times \omega_n^n) \\ &= A_1(\omega_{\frac{n}{2}}^{k}) - \omega_n^kA_2(\omega_{\frac{n}{2}}^{k}) \end{align*}$

所以，如果我们知道两个多项式 $A_1(x)$ 和 $A_2(x)$ 分别在 $(ωn20,ωn21,ωn22,...,ωn2n2−1)(\omega_{\frac{n}{2}}^{0}, \omega_{\frac{n}{2}}^{1}, \omega_{\frac{n}{2}}^{2}, ... , \omega_{\frac{n}{2}}^{\frac{n}{2} - 1})$ 的值，就可以求出 $A (x)$ 在 $ωn0,ωn1,ωn2,...,ωnn−1\omega_n^0, \omega_n^1, \omega_n^2, ..., \omega_n^{n-1}$ 处的值了， $A_1(x)$ 和 $A_2(x)$ 是规模缩小一半的子问题，分治边界 $n = 1$ .
在这里插入图片描述

IFFT

现在我们有了这若干个点的纵坐标，问题来到如何根据这些点的坐标还原答案多项式的系数，这需要用到IFFT(Inverse Fast Fourier Transform)

结论：把多项式 $A (x)$ 的离散傅里叶变换结果作为另一个多项式 $B (x)$ 的系数，取单位根的倒数即 $ωn0,ωn−1,ωn−2,...,ωn−(n−1)\omega_{n}^{0}, \omega_{n}^{-1}, \omega_{n}^{-2}, ..., \omega_{n}^{-(n - 1)}$ 作为 $x$ 代入 $B (x)$ ，得到的每个数再除以 $n$ ，得到的是 $A (x)$ 的各项系数。
（FFT的过程是求y矩阵，IFFT的过程是反过来求a矩阵，求出 $ω\omega$ 矩阵的逆矩阵即可）
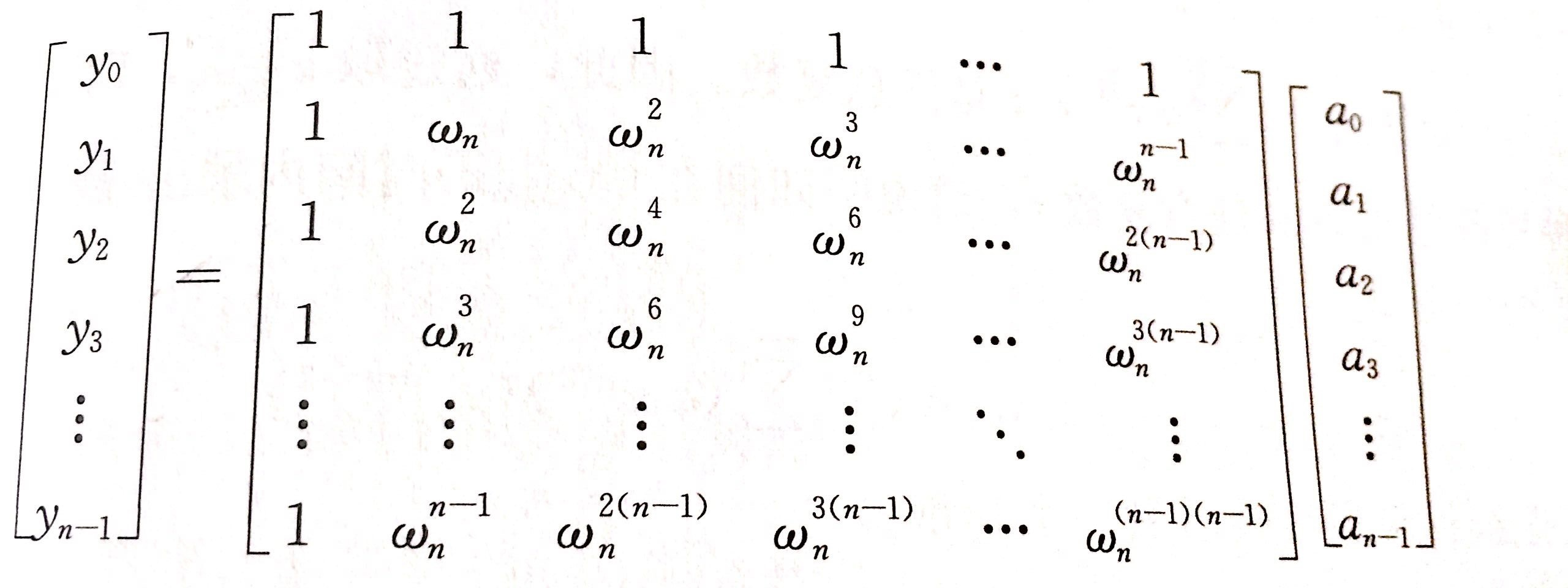
在这里插入图片描述

在这里插入图片描述

朴素版FFT函数代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;const ll N=1000010;
const double pi=acos(-1);
complex<double> a[N],b[N];
ll n,m;inline ll read(){ll x=0,tmp=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') tmp=-1;ch=getchar();}while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}return tmp*x;
}void fft(complex<double> *a,ll n,ll op)
{if(!n) return;complex<double> a0[n],a1[n];for(ll i=0; i<n; i++){a0[i]=a[i<<1];a1[i]=a[i<<1|1];}fft(a0,n>>1,op); fft(a1,n>>1,op);complex<double> W(cos(pi/n),sin(pi/n)*op),w(1,0);for(ll i=0;i<n;i++,w*=W){a[i]=a0[i]+w*a1[i];a[i+n]=a0[i]-w*a1[i];}
}int main()
{n=read(); m=read();for(ll i=0; i<=n; i++) a[i]=read();for(ll i=0; i<=m; i++) b[i]=read();for(m+=n,n=1; n<=m; n<<=1);fft(a,n>>1,1); fft(b,n>>1,1);for(ll i=0;i<n;i++) a[i]*=b[i];fft(a,n>>1,-1);for(ll i=0; i<=m; i++) printf("%.0lf ",fabs(a[i].real()/n));return 0;
}

优化FFT

在进行FFT时，我们要把各个系数不断分组并放到两侧，那么一个系数原来的位置和最终的位置有什么规律呢？

初始位置：0 1 2 3 4 5 6 7
第一轮后：0 2 4 6|1 3 5 7
第二轮后：0 4|2 6|1 5|3 7
第三轮后：0|4|2|6|1|5|3|7

“|”代表分组界限。一个位置a上的数，最后所在的位置是“a二进制翻转得到的数”，例如6(011)最后到了3(110)，1(001)最后到了4(100)。

那么我们可以据此写出非递归版本FFT：先把每个数放到最后的位置上，然后不断向上还原，同时求出点值表示。

void fft(cp *a,int n,int inv)
{int bit=0;while((1<<bit)<n) bit++;for(int i=0;i<n;i++){rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));if(i<rev[i]) swap(a[i],a[rev[i]]);}for(int len=1;len<n;len*=2)//len是准备合并序列的长度的二分之一{cp temp(cos(pi/len),inv*sin(pi/len));for(int i=0;i<n;i+=len*2)//len*2是准备合并序列的长度，i是合并到了哪一位{cp omega(1,0);for(int j=0;j<len;j++,omega*=temp)//只扫左半部分，得到右半部分的答案{cp x=a[i+j],y=omega*a[i+j+len];a[i+j]=x+y,a[i+j+mid]=x-y;}}}
}

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;const ll N=10000010;
const double pi=acos(-1);
ll n,m,limit;
complex<double> a[N],b[N];
ll c[N];inline ll read()
{ll x=0,tmp=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-') tmp=-1;ch=getchar();}while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}return tmp*x;
}inline void write(ll x)
{if(x<0) putchar('-'), x=-x;ll y=10,len=1;while(y<=x) y=(y<<3)+(y<<1), len++;while(len--) y/=10, putchar(x/y+48),x%=y;
}void FFT(complex<double> *a,ll op)
{for(ll i=0; i<limit; i++)if(i<c[i]) swap(a[i],a[c[i]]);for(ll mid=1; mid<limit; mid<<=1){complex<double> W(cos(pi/mid),op*sin(pi/mid));for(ll r=mid<<1,j=0; j<limit; j+=r){complex<double> w(1,0);for(ll l=0; l<mid; l++,w*=W){complex<double> x=a[j+l],y=w*a[j+mid+l];a[j+l]=x+y; a[j+mid+l]=x-y;}}}
}int main()
{n=read(); m=read();for(ll i=0; i<=n; i++) a[i]=read();for(ll i=0; i<=m; i++) b[i]=read();limit=1; ll l=0;while(limit<=n+m)limit<<=1,l++;for(ll i=0;i<limit i++) c[i]=(c[i>>1]>>1)|((i&1)<<(l-1));FFT(a,1); FFT(b,1);for(ll i=0; i<=limit; i++) a[i]*=b[i];FFT(a,-1);for(ll i=0; i<=n+m; i++){write(a[i].real()/limit+0.5);putchar(' ');}return 0;
}