一个很有趣的知识点。
AB=O时:将B进行列分块,B=(β1,β2,…,βn)
AB=A (β1,β2,…,βn)=(O,O,O,O,…,O)
从而,Aβi=O, i=1,2,…,n
即βi是方程组Ax=0的解
则,向量组β1,β2,…,βn可由Ax=0的基础解系线性表出。所以r( (β1,β2,…,βn))≤n-r(A)
即:基础解系的向量个数大于等于βi的总个数。
即:r(A)+r(B) ≤ n
所以,只要有AB=O这个条件,立马用上这个结论。
同时,B的列向量是Ax=0的解,如果B的列向量线性无关,且数目恰好是n-r(A),那么B的列向量就是方程的基础解系了。
AB=0
news/2024/11/28 7:21:06/
相关文章
【NVMe2.0b 3】NVM 控制器架构模型
NVM 控制器架构模型 3.1.1控制器模型3.1.2Controller Types3.1.2.1I/O Controller3.1.2.1.1Command Support3.1.2.1.2Log Page Support3.1.2.1.3Features Support 3.1.2.2Administrative Controller3.1.2.2.1Command Support3.1.2.2.2Log Page Support 3.1.2.3Discovery Contro…
000000000000000000000000
xplatform: 选择交叉编译时的目标 mkspec
prefix :指定 make install 的位置
./configure -release -opensource -confirm-license -xplatform aarch64-linux-gnu-gcc -prefix /opt/aarch64—qt5 -nomake examples -nomake tools -nomake tests -no-op…
【NVMe2.0b 2】NVMe 结构理论
2操作理论
NVM Express 可扩展接口旨在满足使用基于 PCI Express 的固态驱动器或光纤连接设备的存储系统的需求。该接口提供了优化的命令提交和完成路径。它通过支持多达 65,535 个 I/O 队列和每个 I/O 队列多达 64 Ki - 1 个未完成的命令来支持并行操作。此外,还添…
【NVMe2.0b 5】NVM Subsystem
NVM Subsystem 3.2NVM子系统实体3.2.1命名空间3.2.1.1命名空间概述3.2.1.2Valid and Invalid NSIDs3.2.1.3Allocated and Unallocated NSID Types3.2.1.4Active and Inactive NSID Types3.2.1.5NSID and Namespace Relationships3.2.1.7I/O Command Set Associations 3.2.2NVM …
大数据(0b)离线数据仓库
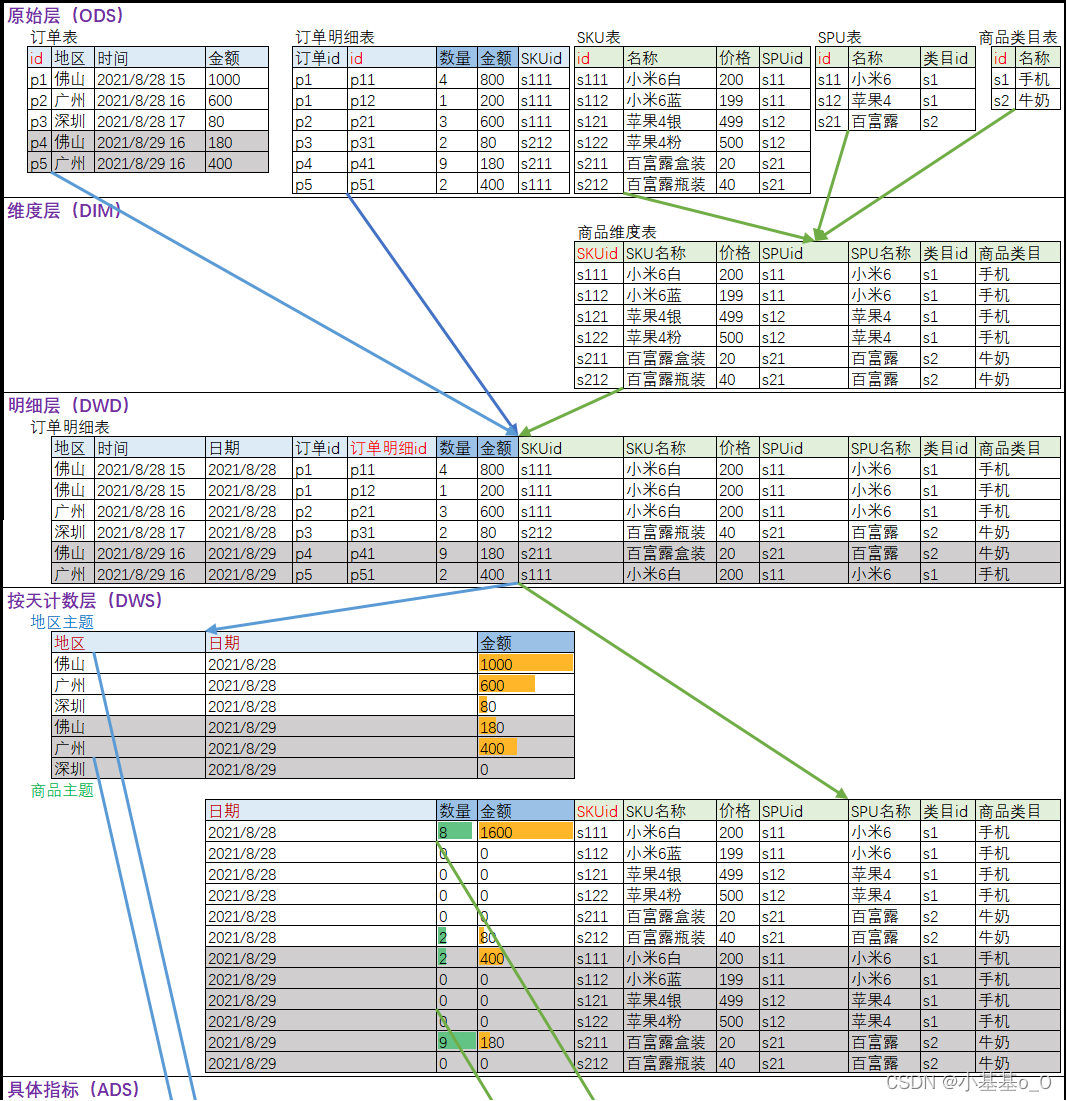
文章目录 1、数据库 & 数据仓库2、OLTP & OLAP3、范式理论4、维度表 & 事实表4.1、维度表4.2、事实表 5、星型模型、雪花模型、星座模型6、数仓分层6.1、命名规范6.2、合并维度表 and 维度缩减(ODS>DIM)6.3、数据处理(ODS>…
【NVMe2.0b 14-8】Set Features(下篇)
Set Features 5.27.1.13Host Controlled Thermal Management (Feature Identifier 10h), (可选)5.27.1.14Non-Operational Power State Config (Feature Identifier 11h), (可选)5.27.1.15Read Recovery Level Config (Feature Identifier 12h)5.27.1.16Predictable Latency Mo…
【NVMe2.0b 13】NVMe 标准数据结构
NVMe 标准数据结构 4数据结构4.1数据布局4.1.1Physical Region Page Entry and List4.1.2Scatter Gather List (SGL)4.1.2.1SGL示例 4.1.3Metadata Region (MR) 4.2Feature值4.3Identifier的格式与布局4.3.1PCI Vendor ID (VID) 和 PCI Subsystem Vendor ID (SSVID)4.3.2Serial…
【NVMe2.0b 9】控制器初始化过程
控制器初始化过程 3.5控制器初始化3.5.1基于内存传输的控制器初始化3.5.2基于消息传输的控制器初始化3.5.3Controller Ready Modes During Initialization3.5.4初始化过程中的Controller Ready Timeouts3.5.4.1Handling Errors During Initialization 3.5控制器初始化
本节介绍…