（一）、树型结构

1.树的定义:

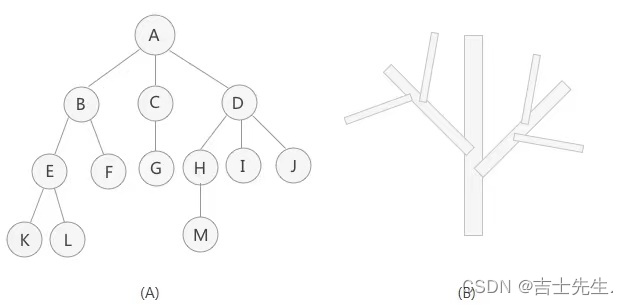
树是一种数据结构，它是由n(n≥0)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：
每个结点有零个或多个子结点(n>=0)；没有父结点的结点称为根节点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树。（一对多的关系，。没有节点这一说）

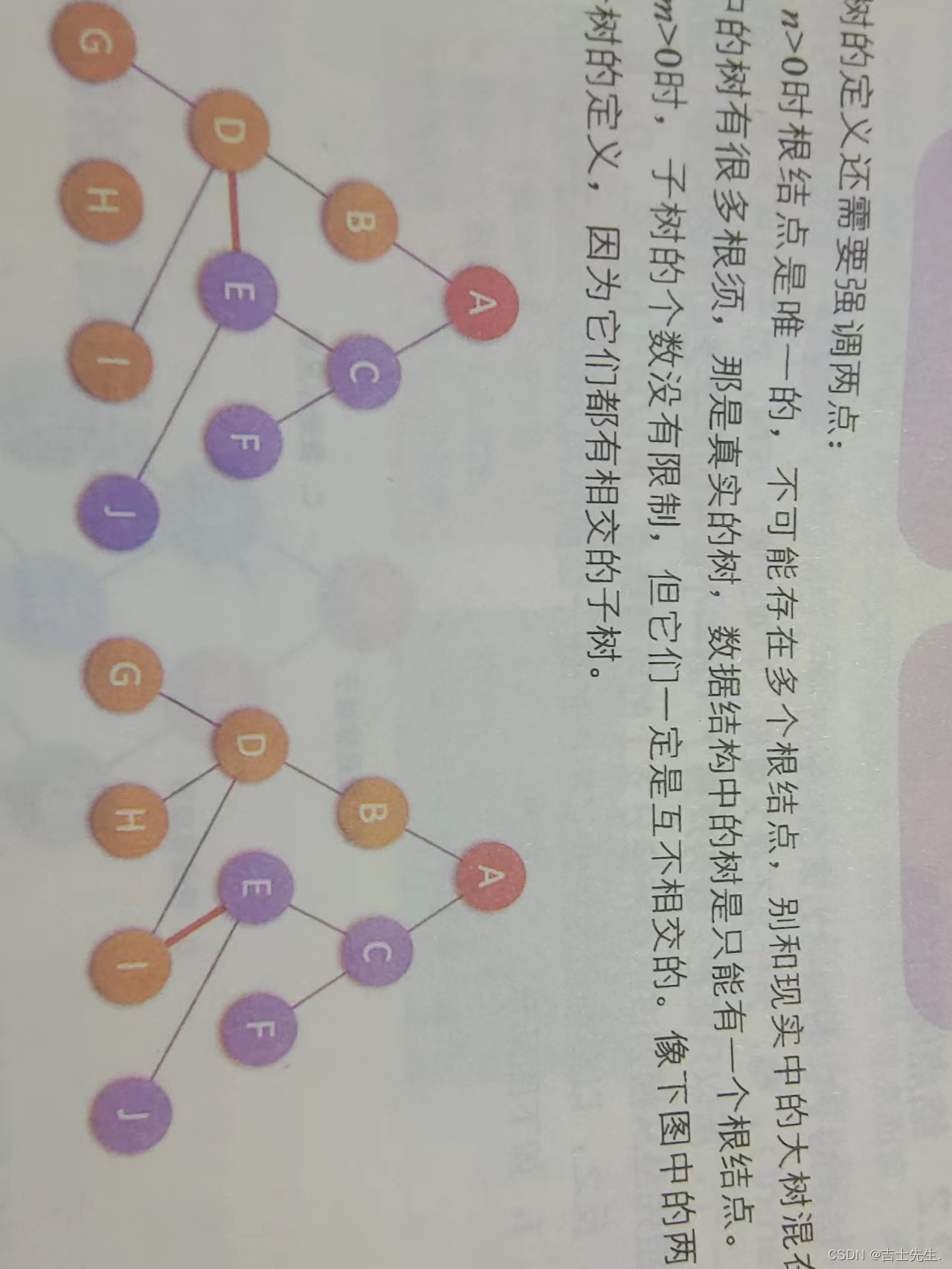
2.树需要注意的地方

1.一个树只能有一个根结点，但可以有多个子结点。
2.子结点的个数没有限制，但是子结点一定不能相交互。

3.结点的分类:（树的度 节点的度）

树的结点包含一个数据元素及若干个指向其子树的分支。结点拥有的子树数称为结点的度（Degree）。度为0的结点称为叶结点（Leaf）或终端结点；度不为0的结点称为非终端结点或分支支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。

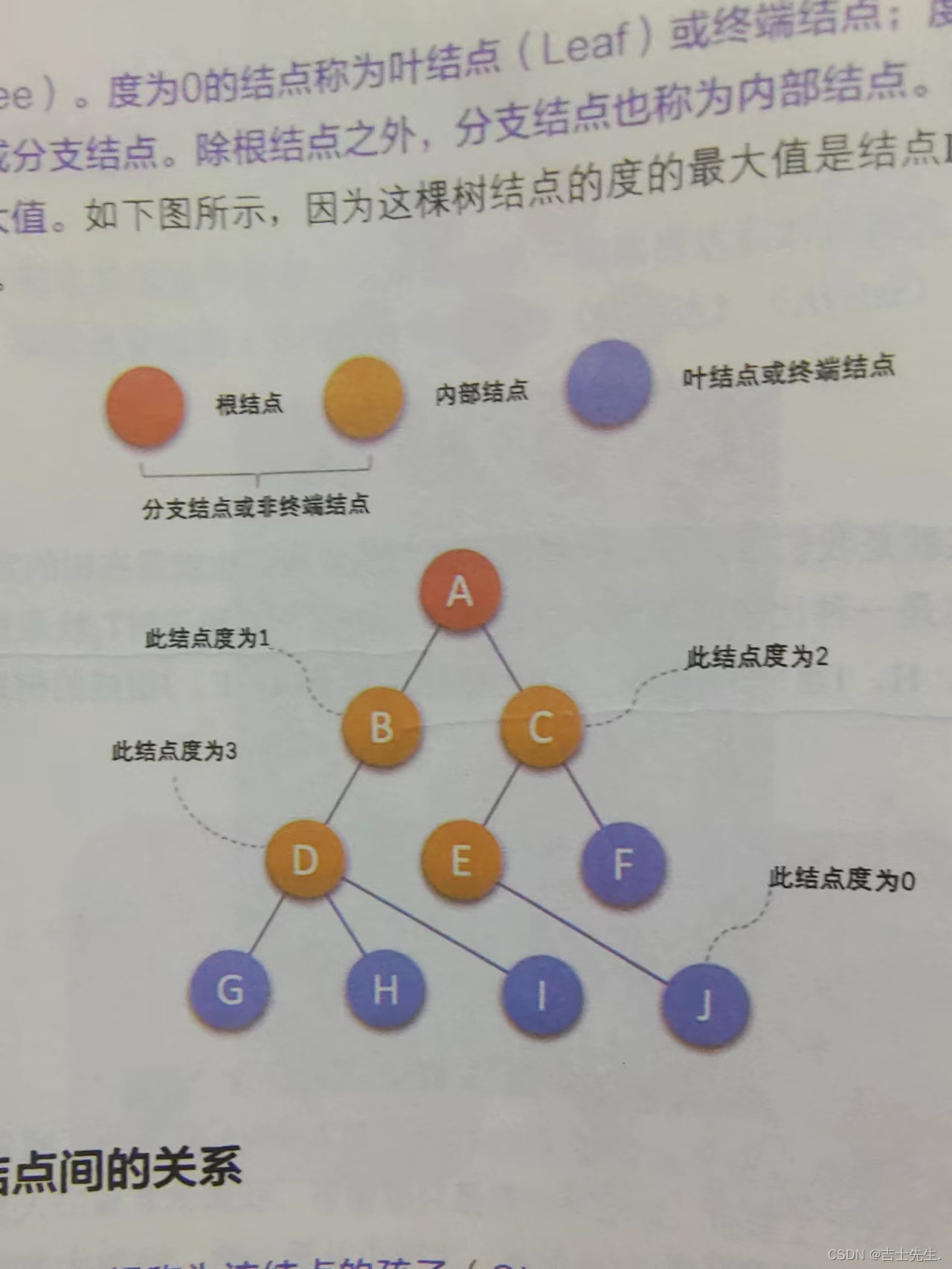
4.结点间的关系:

结点的子树的根称为该结点的孩子（Child），相应的，该结点称为孩子的双亲（Parent）（注意是双亲，不是单亲）。同一个双亲的孩子之间互称兄弟（Sibling）。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中的任一结点都称为该结点的子孙。

5.树的其他相关概念:

结点的层次（Level）从根开始定义起，根为第一层，根的孩子为第二层。双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的深度（Depth）或高度。

如果将树中结点的各子树看成从左至右是有次序的，不能互换，则称该树为有序树，否则为无序树。
森林（Forest）是m（m>=0）棵互不相交的树的集合。

根结点没有父结点，其他的结点都有一个父结点，
子结点 ：父结点的下一层。
叶子结点：没有子结点的结点。
结点的度：结点的子结点数。
树的度：最多的叶结点的度。
结点的层：根结点为1，依次类推。
高度 ：树的最大层。
森林：

(二)、二叉树

二叉树的定义:
二叉树的每个结点的子结点最多只有两个子树的树结构。也就是说树的度为2
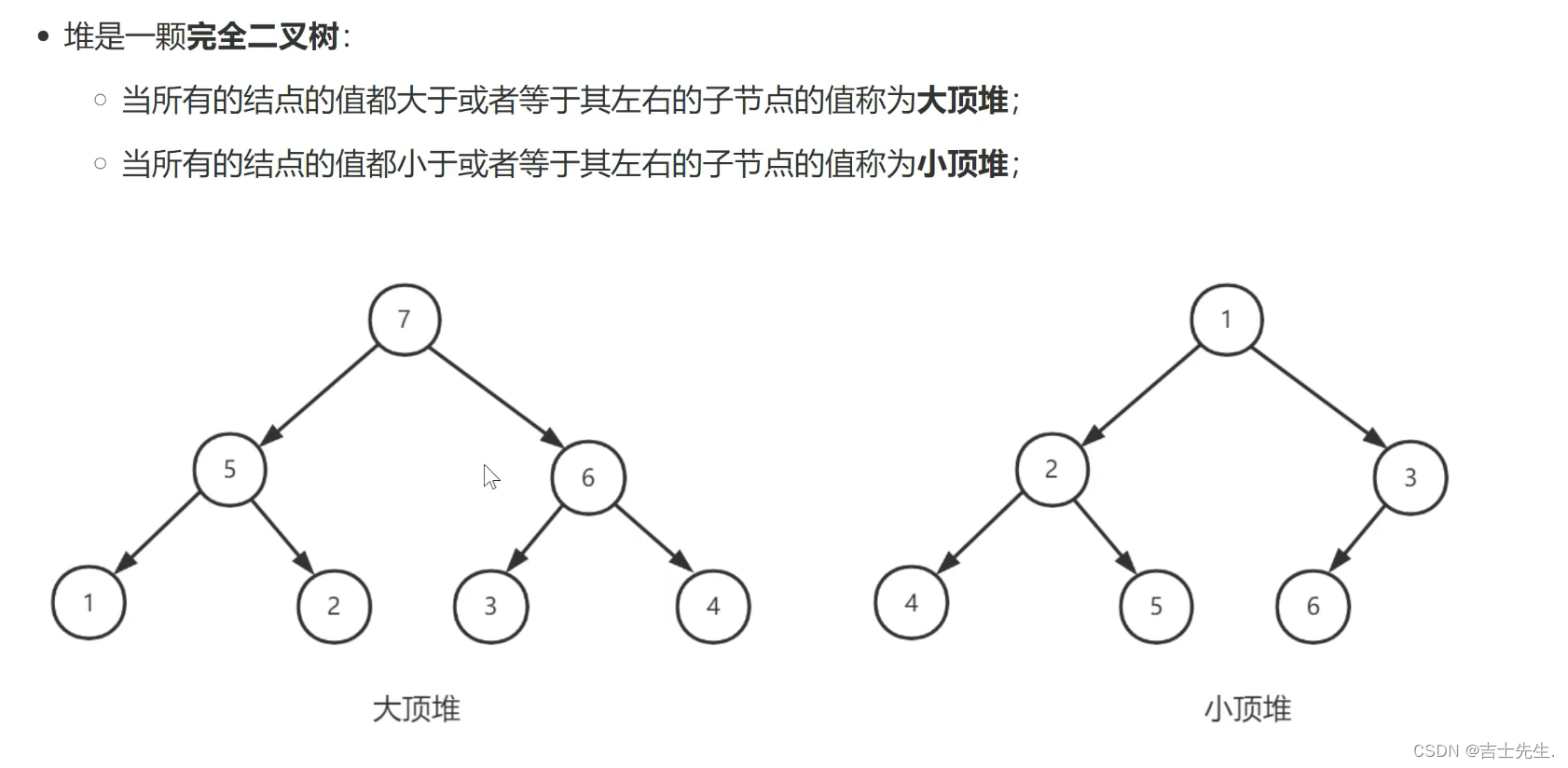
满二叉树的定义:
每一层的结点树都达到最大值。
完全二叉树的定义:
设二叉树的深度为k,除第k层外，其他各层(1~（k-1）)的结点数都达到最大值。第k层所有的结点都连续集中在最左边，这就是完全二叉树。

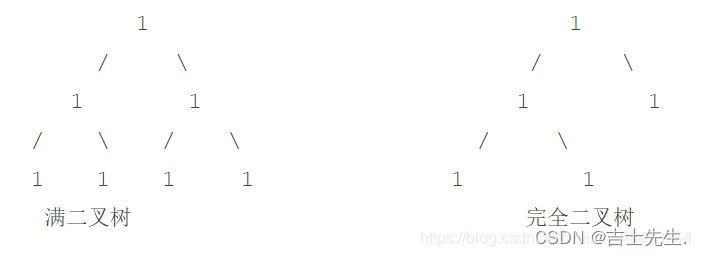
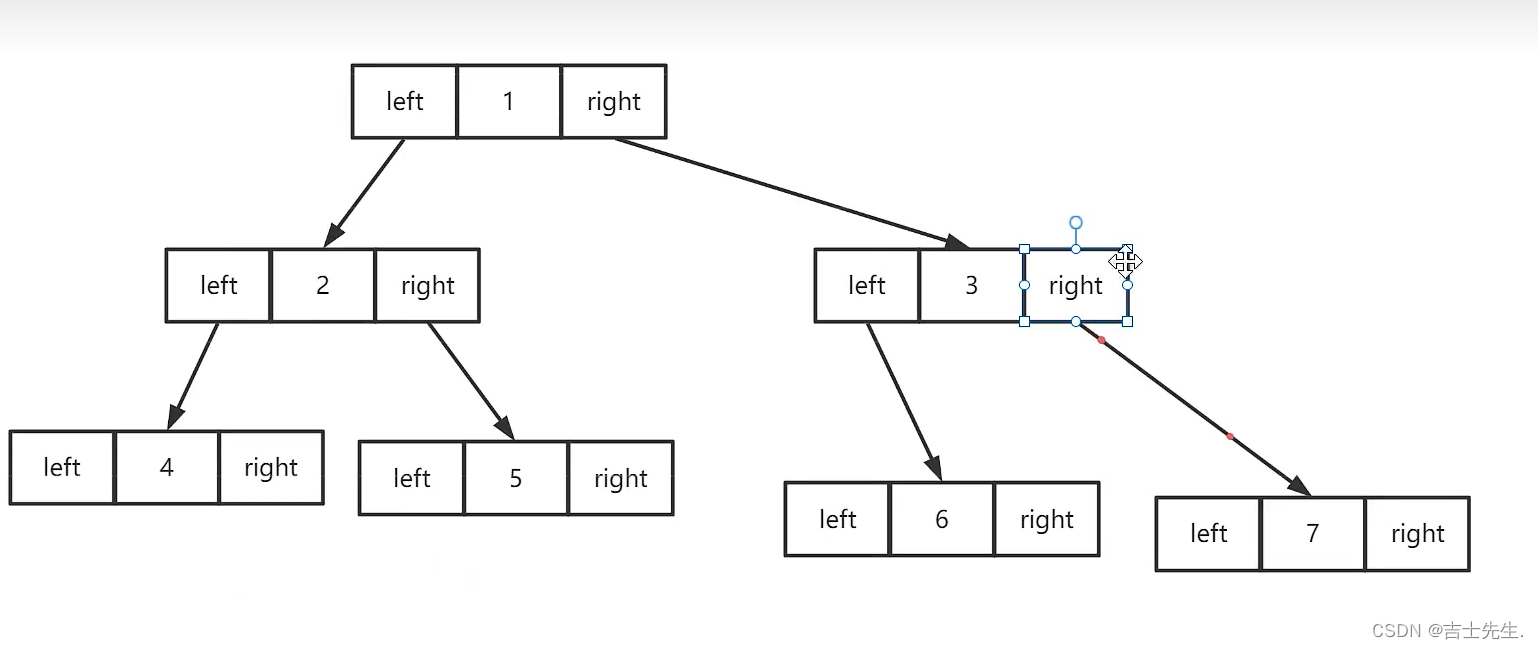
1.二叉树的创建:

创建结点:

 public class Node{//数值Object item;//左右子结点Node left;Node right;public Node(Object item){this.item=item;}}

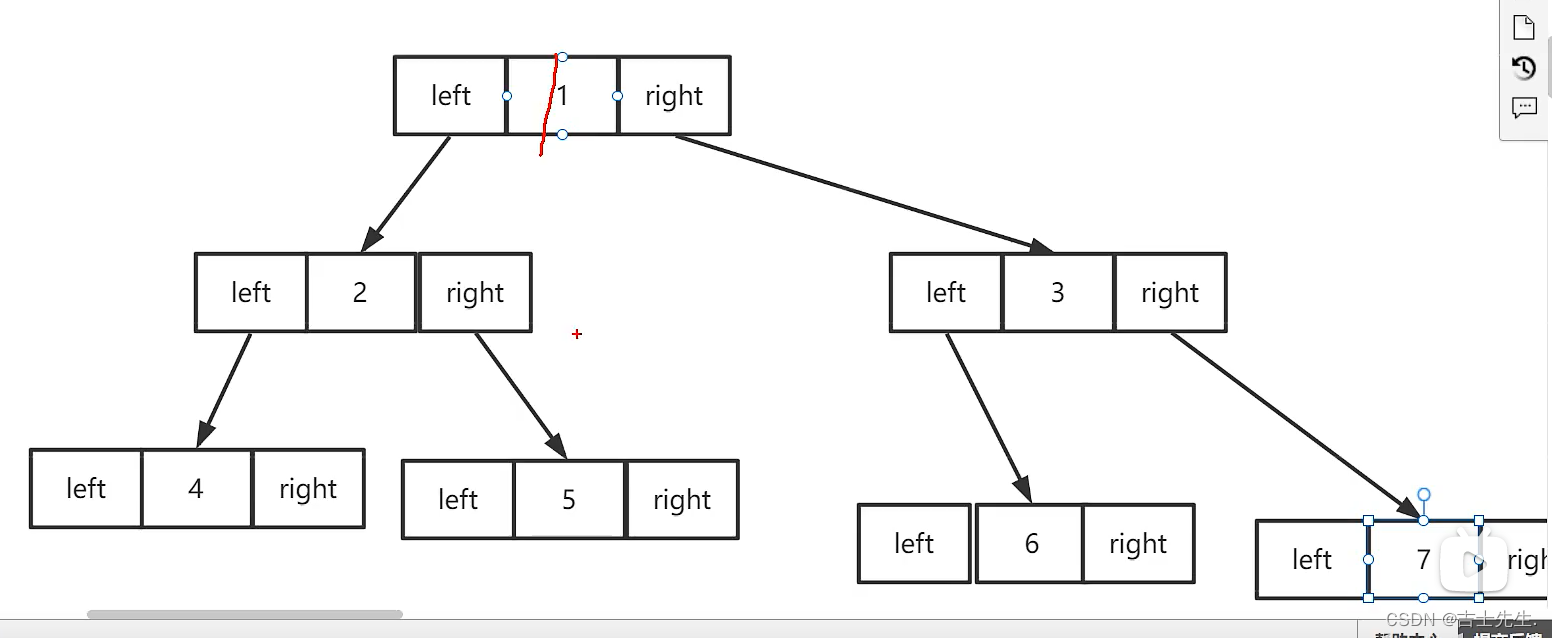
创建树:

 public void CreateTree() {//创建根节点root=new Node(1);//第二层//创建左子结点Node Left=new Node(2);//创建右子结点Node Right=new Node(3);//进行关联root.left=Left;root.right=Right;//第三层Node Left2=new Node(4);//创建右子结点Node Right2=new Node(5);//进行关联root.left.left=Left2;root.left.right=Right2;//第三层Node Left3=new Node(6);//创建右子结点Node Right3=new Node(7);//进行关联root.right.left=Left3;root.right.right=Right3;}

前序遍历:

  public void ShowTree(Node node){if(node==null){return;}//遍历根节点System.out.println(node.item);//遍历左子树ShowTree(node.left);//遍历右子树ShowTree(node.right);}

中序遍历:

  public void MidShowTree(Node node){if(node==null){return;}//遍历左子树MidShowTree(node.left);//遍历根节点System.out.println(node.item);//遍历右子树MidShowTree(node.right);}

后序遍历:

 public void FinShowTree(Node node){if(node==null){return;}//遍历左子树FinShowTree(node.left);//遍历右子树FinShowTree(node.right);//遍历根节点System.out.println(node.item);}

层次:

   public void LeveTree(Node node){//创建队列;ArrayDeque <Node> ad=new ArrayDeque<>(10);//加入根节点ad.add(node);while (!ad.isEmpty()) {Node n=ad.poll();System.out.println(n.item);//左子树放到队列if(n.left!=null){ad.add(n.left);}//将右子树放到队列中去if(n.right!=null){ad.add(n.right);}}}

全部代码:

1.1.全部代码:

import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {public static void main(String []avgs){Tree t=new Tree();t.CreateTree();t.ShowTree(t.root);System.out.println("==============");t.MidShowTree(t.root);System.out.println("==============");t.FinShowTree(t.root);System.out.println("==============");t.LeveTree(t.root);System.out.println("==============");Tree.Node result=t.Select(t.root,13);if(result==null){System.out.println("无相等的结果");}else{System.out.println("有相等的结果为:"+result.item);}System.out.println("===========");t.Delete(t.root,1);t.LeveTree(t.root);}
}

import java.util.ArrayDeque;public class Tree{//定义一个根节点Node root;//创建结点public static class Node{//数值Object item;//左右子结点Node left;Node right;//判断当前左右指针是否线索化boolean isLeftLine=false;boolean isRightLine=false;public Node(Object item){this.item=item;}}//创建一棵树public void CreateTree() {//创建根节点root=new Node(1);//第二层//创建左子结点Node Left=new Node(2);//创建右子结点Node Right=new Node(3);//进行关联root.left=Left;root.right=Right;//第三层Node Left2=new Node(4);//创建右子结点Node Right2=new Node(5);//进行关联root.left.left=Left2;root.left.right=Right2;//第三层Node Left3=new Node(6);//创建右子结点Node Right3=new Node(7);//进行关联root.right.left=Left3;root.right.right=Right3;}//前序遍历public void ShowTree(Node node){if(node==null){return;}//遍历根节点System.out.print(node.item+" ");//遍历左子树ShowTree(node.left);//遍历右子树ShowTree(node.right);}//中序public void MidShowTree(Node node){if(node==null){return;}//遍历左子树MidShowTree(node.left);//遍历根节点System.out.print(node.item+" ");//遍历右子树MidShowTree(node.right);}//后序遍历public void FinShowTree(Node node){if(node==null){return;}//遍历左子树FinShowTree(node.left);//遍历右子树FinShowTree(node.right);//遍历根节点System.out.print(node.item+" ");}//层次遍历:public void LeveTree(Node node){//创建队列;ArrayDeque <Node> ad=new ArrayDeque<>(10);if(node==null){System.out.println("树里面已经没有结点了");return;}//加入根节点ad.add(node);while (!ad.isEmpty()) {Node n=ad.poll();System.out.print(n.item+" ");//左子树放到队列if(n.left!=null){ad.add(n.left);}//将右子树放到队列中去if(n.right!=null){ad.add(n.right);}}}//查找元素:public Node Select(Node node,Object t){Node target=null;if(node==null){return null;}else{if(node.item==t){return node;}else{//从左子树进行遍历target=Select(node.left,t);//判断是否找到了结果if(target!=null){return target;}//从右子树进行遍历target=Select(node.right,t);//判断是否找到了结果if(target!=null){return target;}return null;}}}//删除元素:public void Delete(Node node,Object t){if(node==null){return;}//判断根节点if(node==root&&root.item==t){this.root=null;}//判断子结点是否为nullif(node.left!=null){if(node.left.item==t){//删除左子结点node.left=null;return;}else{Delete(node.left,t);}}//判断右子结点if(node.right!=null){if(node.right.item==t){//删除右子结点node.right=null;return;}else{Delete(node.right,t);}}}//二叉树的深度public int MaxDelth(Node node){if(node==null){return 0;}int leftDeth=0;int rightDeth=0;//获取左子树的高度if(node.left!=null){leftDeth=MaxDelth(node.left);}//获取右子树的高度if(node.right!=null){rightDeth=MaxDelth(node.right);}//判断最大层次关系if(leftDeth>rightDeth){return leftDeth+1;}else{return rightDeth+1;}}}

2.二叉树的遍历规则：

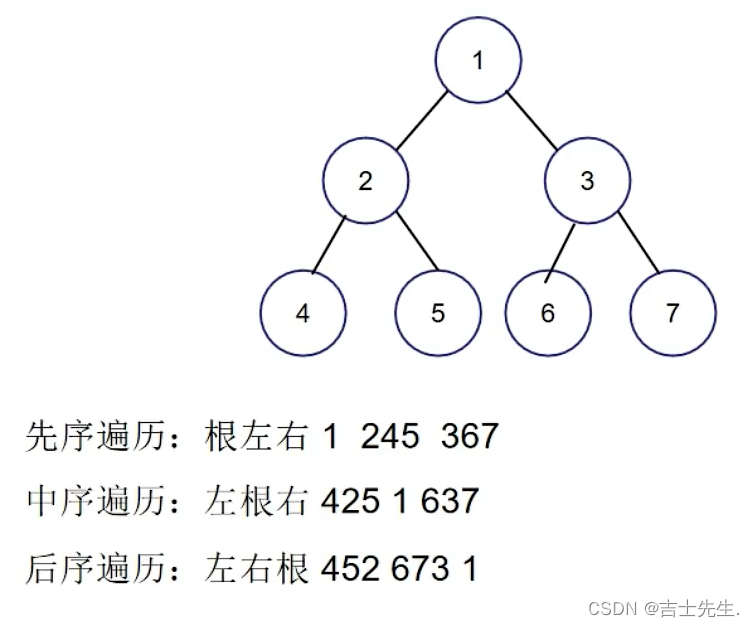
前序遍历: 根结点-左子树-右子树；
中序遍历:左子树-根结点-右子树;
后序遍历:左子树-右子树-根节点；

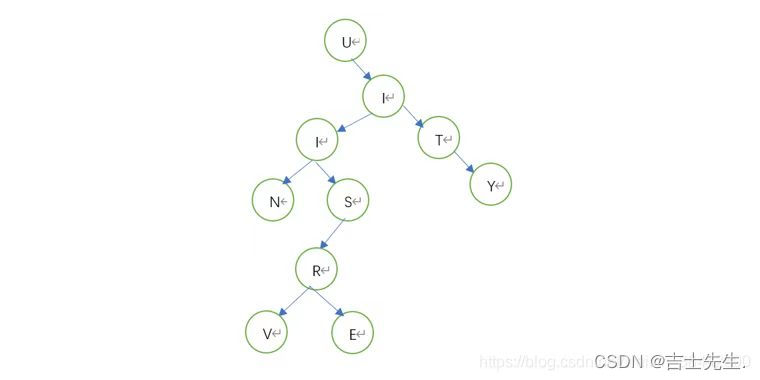
前序遍历:

前序遍历的遍历顺序是根左右。
我们首先从根节点U出发，由于它是根节点因此U排在首位，得到顺序U。
然后去找U的左节点，发现U没有左节点，于是去找U的右分支，得到顺序UI。
发现I有左节点I，得到顺序UII。
发现I有左节点N，得到顺序UIIN。
发现I有右节点S，得到顺序UIINS。
发现S有左节点R，得到顺序UIINSR。
发现R有左节点V，得到顺序UIINSRV。
发现R有右节点E，得到顺序UIINSRVE。
发现I有右节点T，得到顺序UIINSRVET。
发现I有右节点Y，得到顺序UIINSRVETY。
前序遍历从根节点出发，然后去找他的左节点，再找右节点，深度优先。

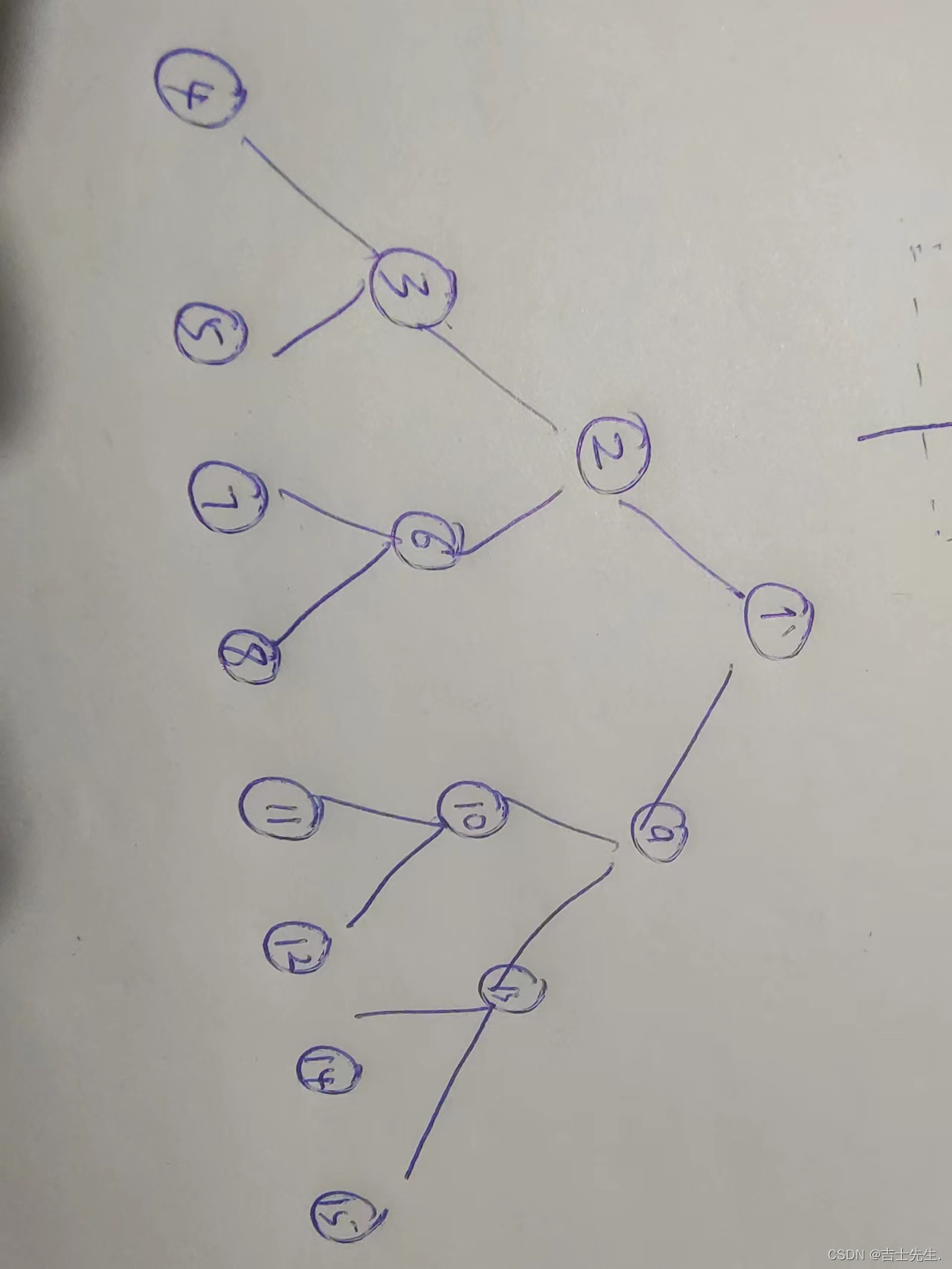
（三）、数组实现二叉树

n是下标不是数字哈
1.必须是完全二叉树.
2.左子节点是2n+1;
3.右子节点是2n+2;
4.父类子结点是(n-1)/2;
5.n代表从第几个(n初始化为0)；

1.数组二叉树数组的遍历

public class array {int []elem;public array(int []s){this.elem=s;}//实现先序遍历public void preT(int idex){if(idex>=elem.length){return;}//遍历当前结点System.out.print(elem[idex]+" ");//遍历左节点preT(2*idex+1);//遍历右节点preT(2*idex+2);}//遍历中序public void midT(int idex){if(idex>=elem.length){return;}//遍历左节点midT(2*idex+1);//遍历当前结点System.out.print(elem[idex]+" ");//遍历右节点midT(2*idex+2);}//遍历后序public void laterT(int idex){if(idex>=elem.length){return;}//遍历左节点laterT(2*idex+1);//遍历右节点laterT(2*idex+2);//遍历当前结点System.out.print(elem[idex]+" ");}}

import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {public static void main(String []avgs){array s1=new array(new int[]{1,2,3,4,5,6,7});s1.preT(0);System.out.println("===========");s1.midT(0);System.out.println("===========");s1.laterT(0);}
}

2.大堆顶的实现及其排序

import org.jetbrains.annotations.NotNull;import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {public static void main(String []avgs){int []arr=new int[]{9,19,3,2,18,7,8,25,29,4,20};//构造二叉树的guize//左结点 2*n+1;//右节点 2*n+2;//最后一个非叶子结点 :(arr.length-1)/2//展现大顶堆for (int i = (arr.length-1)/2; i >=0; i--) {Dui(arr,i);}for (int i = 0; i <arr.length; i++) {System.out.print(arr[i]+" ");}//实现大顶堆的排序      错错错//        for (int i = (arr.length-1)/2; i >=0; i--) {
//            PaiDui(arr,i,arr.length);
//        }
//        //从数组的最后元素开始排序遍历
//
//        for (int last=arr.length-1; last >=0 ; last--) {
//            int temp=arr[0];
//            arr[0]=arr[last];
//            arr[last]=temp;
//            //调用大堆顶排序的方法
//            PaiDui(arr,0,last);
//        }
//        for (int i = 0; i <arr.length; i++) {
//            System.out.print(arr[i]+" ");
//        }}//构造大顶堆public static void Dui(int @NotNull []arr, int idex){//计算左子树的位置int left=2*idex+1;//计算右子树的位置int right=2*idex+2;//假如说子结点超过数组的位置，那么就退出if(left>arr.length||right>arr.length){return;}//比较大小int max=idex;if(arr[left]>arr[max]){max=left;}if(arr[right]>arr[max]){max=right;}if(max!=idex){int temp;temp=arr[idex];arr[idex]=arr[max];arr[max]=temp;//还要向下进行比较Dui(arr,max);}}//构造大顶堆且进行排序public static void PaiDui(int []arr,int idex,int size){//计算左子树的位置int left=2*idex+1;//计算右子树的位置int right=2*idex+2;//假如说子结点超过数组的位置，那么就退出if(left>size||right>size){return;}//比较大小int max=idex;if(arr[left]>arr[max]){max=left;}if(arr[right]>arr[max]){max=right;}if(max!=idex){int temp;temp=arr[idex];arr[idex]=arr[max];arr[max]=temp;//还要向下进行比较PaiDui(arr,max,size);}}
}

(四).二叉查询树

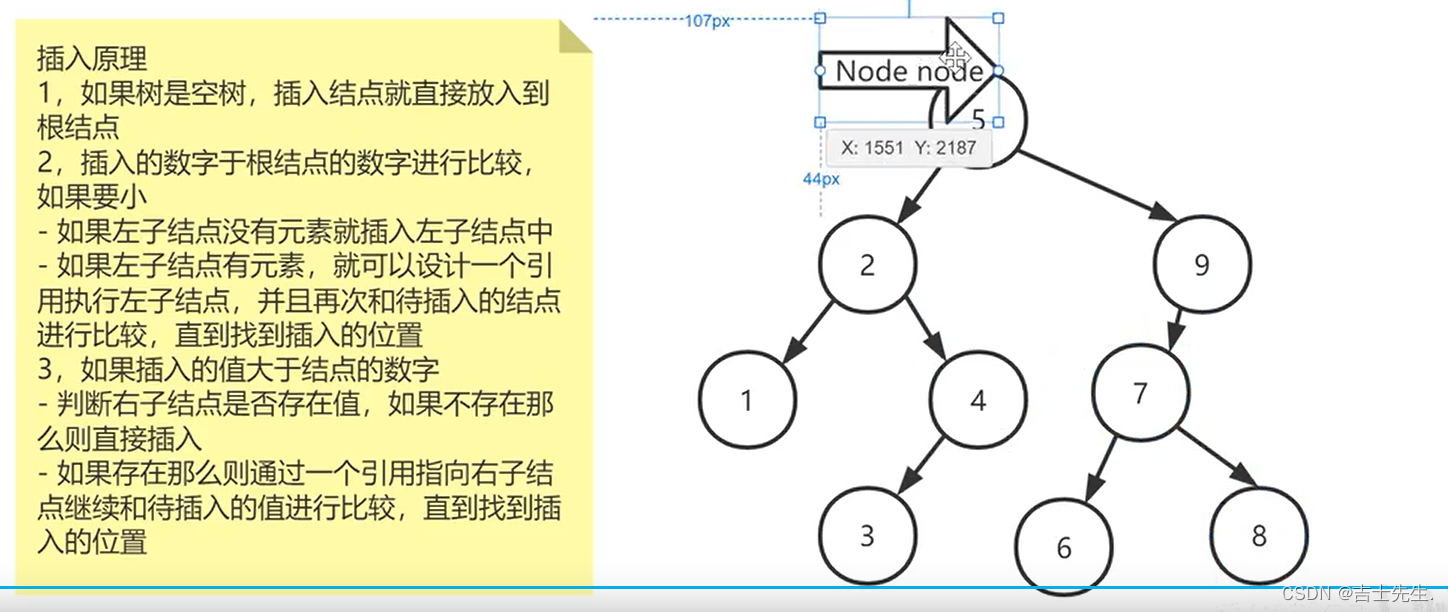
1.二叉查找树的插入原理

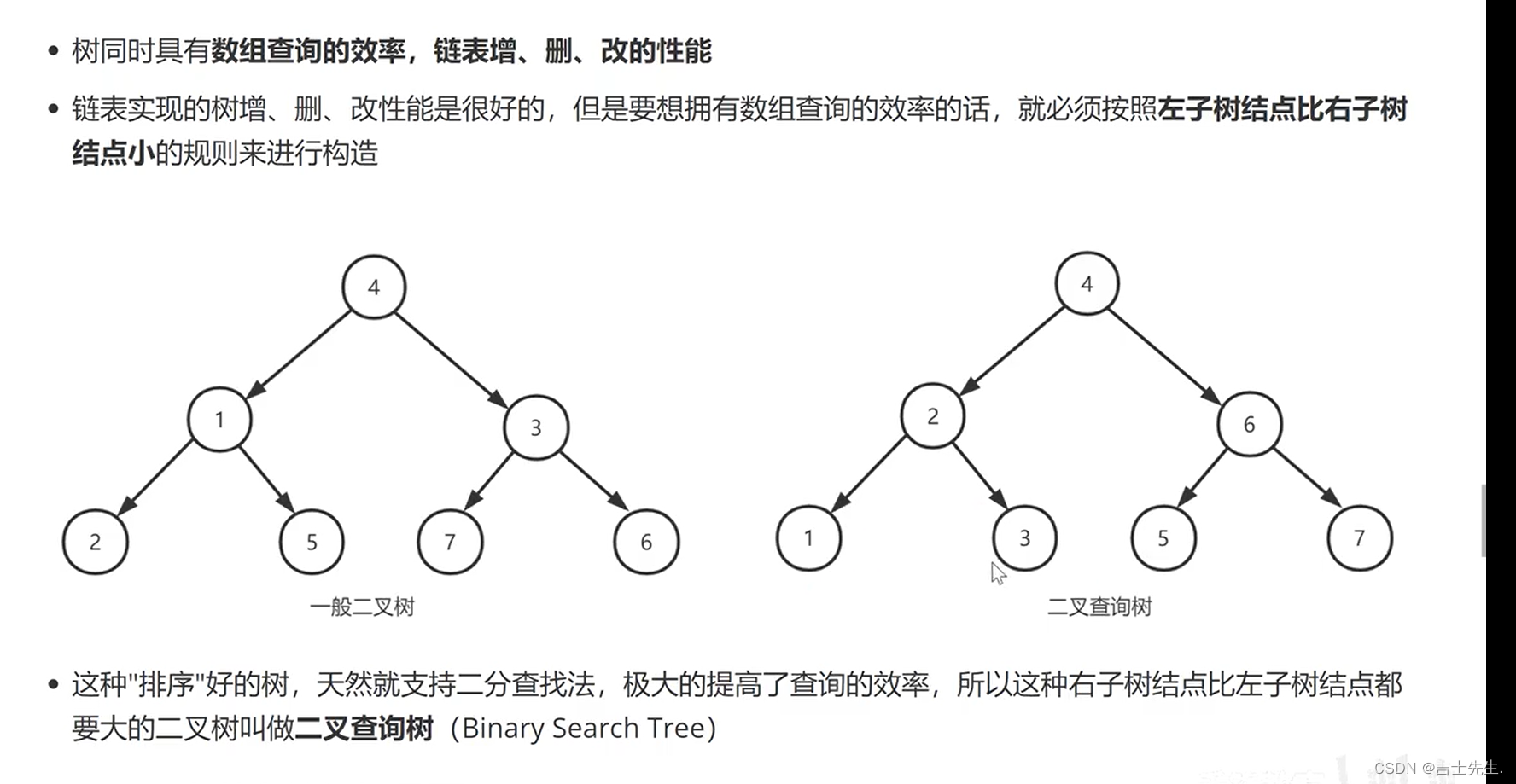
二叉树的插入原理:
假如说是空树。

1.那么插入的结点直接放到根节点的位置

假如说插入的数比父节点要小。

  1.如果左字节点没有元素，那么就插入左子树。2.如果左子结点有元素。那么就设计一个引用执行左结点，

并且再次和待插入的结点进行比较，直到找到插入的位置。

如果插入的数比父节点要大。

1.如果右边不存在元素，那么就插入右子树。
2.如果右结点有元素那么 就引用一个执行右结点，并且再次和待插入的结点进行比较，直到找到插入的位置。

2.二叉查询树的顺序遍历:

使用树的中序遍历，即可达到二叉查询树的顺序遍历

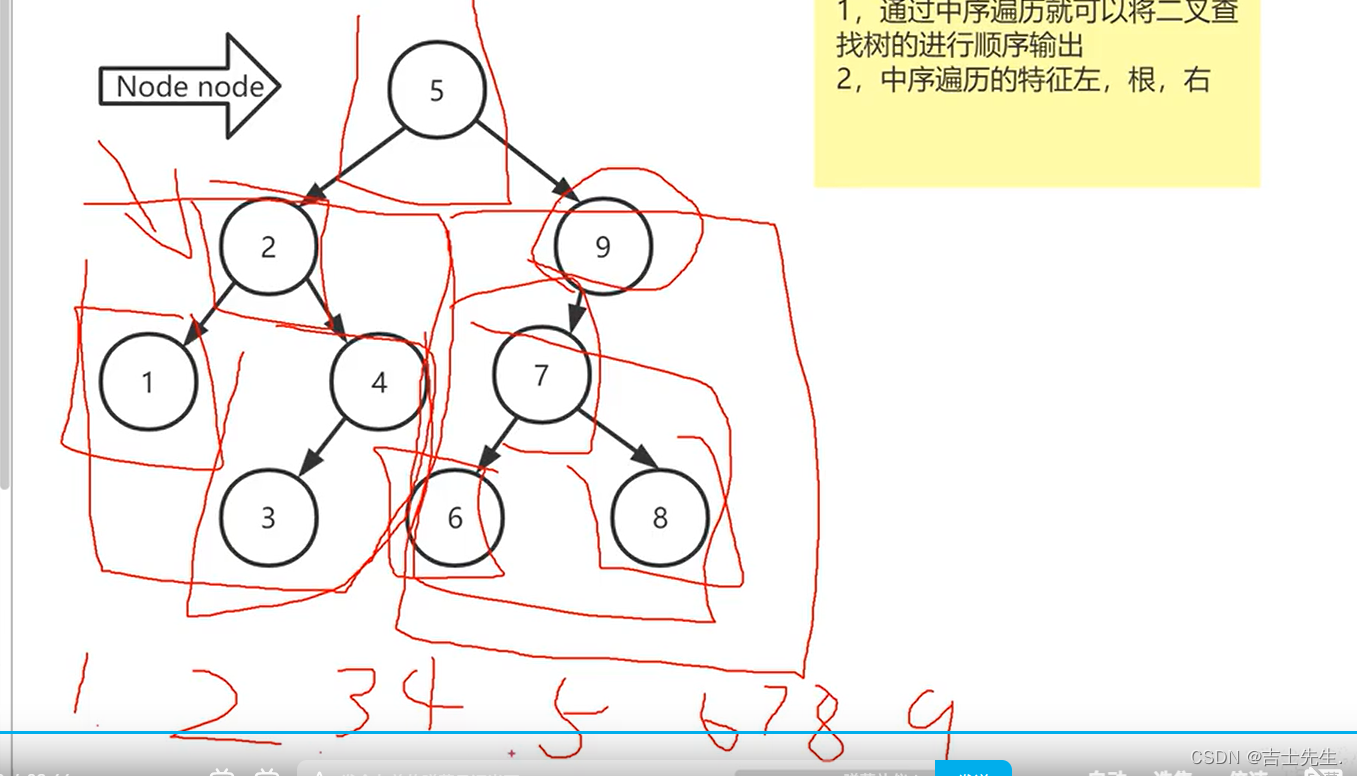
3.二叉查询树的查找原理

1.提供一个你要查找的值。
2.假如说查找的值比结点大，那么就走右子树，假如说比结点小，那么就走左子树。

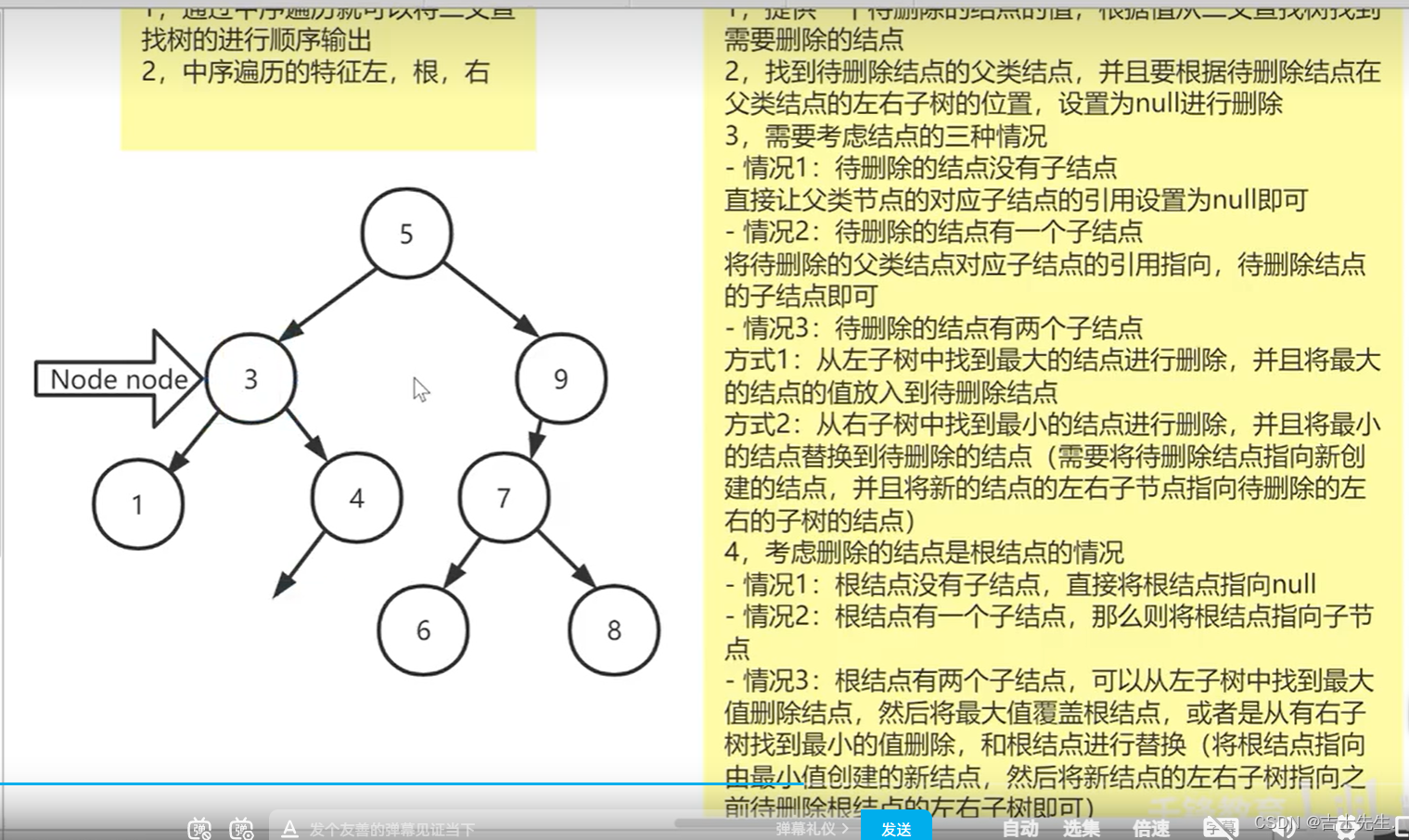
4.二叉查询树的删除原理

1.提供一个待删除结点的值，根据值从二叉树找到需要删除的值的结点。
2.找到待删除结点的父类结点，并且要根据待删除的点在父类的左右子树的位置，设置为null进行删除，
3.需要考虑结点的三种情况:

情况一：待删除的结点没有子结点直接让父类结点的对应子结点的引用设置为null情况二:待删除的结点有一个子结点将待删除的父类结点对应的子结点的引用指向，待删除的结点的子结点即可。情况三：待删除的结点有两个子结点   1.从左子树中找到最小的结点进行删除，并且将最大的结点的值覆盖到待删除结点。
2.从右子树找到最小的结点进行删除，并且将最小的结点替换到待删除的结点（需要将待删除的结点指向新创建的结点）	情况四:考虑删除的结点是根节点:1.根结点没有子结点，直接将根节点指向null
2.根结点有一个子结点，直接将根节点指向子结点。
3.跟结点有两个子结点，可以从左子树中找到最大值删除结点，然后然后将最大值覆盖根节点。或则从右节点找到最小值和跟根节点进行替换（需要将跟结点指向新创建的结点，然后将新结点分别指向左右子树即可）	

5.增删改查（全部代码）

import java.awt.*;public class TreeSelect {//创建树结点public static class Node {Node left;Node right;int value;public Node(int value) {this.value = value;}}//设置根结点；Node root;//构造查询二叉树public void insert(int value) {//假如说根结点为空，那么直接把值给根节点if (root == null) {root = new Node(value);} else {//声明一个游标结点，开始指向根节点Node idex = root;while (true) {//假如说插入的值小于游标的值if (value < idex.value) {//假如说游标左子结点没有值了,那么就把该值给游标的左边if (idex.left == null) {idex.left = new Node(value);break;} else {//假如说游标左子节点有值的话，那么就把游标指向游标的左子节点idex = idex.left;}} else {//如果游标右子节点没有值的话if (idex.right == null) {idex.right = new Node(value);break;} else {//如果不为空，那么就游标指向游标的右节点idex = idex.right;}}}}}//实现中序遍历public void MidTraversal(Node node) {if (node == null) {return;}//遍历左结点MidTraversal(node.left);//输出中结点System.out.print(node.value + " ");//输出右结点MidTraversal(node.right);}//二叉树的删除public static int LEFT = 0;public static int RIGHT = 1;public void deleteNdde(int value) {//定义游标从根结点开始查询Node idex = root;//定义目标结点.Node target = null;//定义目标结点的父类结点Node parent = null;//定义目标结点的类型int nodeType = 0; //0代表左子结点，1代表右子结点//==========查值while (idex != null) {//假如说游标的值等于删除的值if (idex.value == value) {//找到了结点target = idex;break;} else if (value < idex.value) {//假如说删除的值小于游标的值//保存父节点parent = idex;//将游标节点指向左子节点idex = idex.left;nodeType = LEFT;} else {//保存父节点parent = idex;//将游标节点指向右子节点idex = idex.right;nodeType = RIGHT;}}if(target==null){System.out.println("没有找到要删除的结点");}//==========删除结点的三种情况//情况一：没有子结点if (target.left == null && target.right == null) {if(parent==null){  //假如跟结点//直接将rroot为空root=null;return;}//判断目标值的结点是左子节点还是右子节点if (nodeType == LEFT) {//将父类的左子节点设置为nullparent.left = null;} else {parent.right = null;}} else if (target.left != null && target.right != null) { //假如说有两个子结点//从目标值的右子树方法中查找最小值的方法Node min=target.right;//遍历左子树while (min.left!=null){min=min.left;}//将最小的结点进行删除deleteNdde(min.value);//将待删除的结点与最小值进行替换target.value=min.value;} else {//假如只有一个子结点的情况if(parent==null){ //加入删除根节点if(target.left!=null){root=target.left;}else{root=target.right;}return;}if (nodeType == LEFT) {if (target.left != null) {//将父类的子结点指向待删除结点的左子节点parent.left = target.left;} else {//将父类的子节点指向待删除结点的右子结点parent.left = target.right;}} else {if (target.left != null) {//将父类的子结点指向待删除结点的左子节点parent.right = target.left;} else {//将父类的子节点指向待删除结点的右子结点parent.right = target.right;}}}}
}

import org.jetbrains.annotations.NotNull;import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.sql.SQLOutput;
import java.util.*;
import java.awt.*;
import java.lang.Math;
public class hello {public static void main(String []avgs){int []arr=new int[]{5,2,1,4,3,9,7,6,8};TreeSelect ts=new TreeSelect();//将二叉树构造成查询二叉树for(int i=0;i<arr.length;i++){ts.insert(arr[i]);}ts.deleteNdde(11 );//对查询二叉树进行遍历ts.MidTraversal(ts.root);}
}