描述
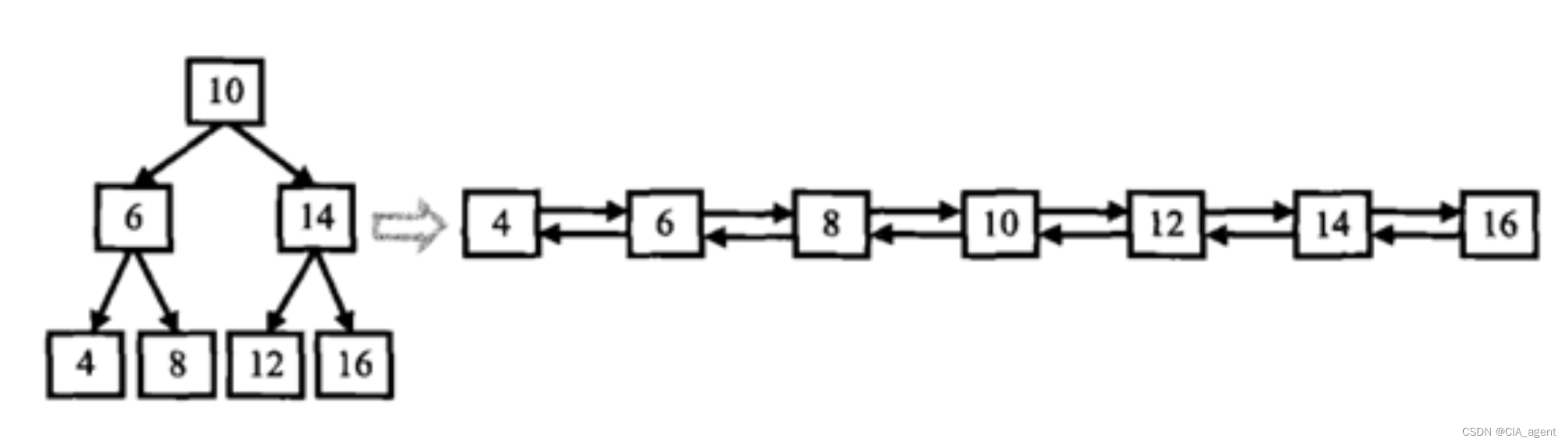
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

数据范围：输入二叉树的节点数 0≤n≤1000，二叉树中每个节点的值 0≤val≤1000，要求：空间复杂度 O(1)（即在原树上操作），时间复杂度 O(n)

注意:
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构
4.你不用输出双向链表，程序会根据你的返回值自动打印输出
输入描述：
二叉树的根节点
返回值描述：
双向链表的其中一个头节点。

示例1
输入：
{10,6,14,4,8,12,16}
返回值：
From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;
说明：
输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。

示例2
输入：
{5,4,#,3,#,2,#,1}
返回值：
From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;
说明：
5
/
4
/
3
/
2
/
1
树的形状如上图

思路：最常规的思路就是中序遍历，对于BST 数，中序遍历就是一个有序的列表，然后把列表转成一个双向队列就ok，由于题目要求空间复杂度 O(1), 我们可以在中序遍历的时候对原有的树做一些变换，在数的基础上进行调整，这样就不用再申请额外的空间了。

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None#
# 
# @param pRootOfTree TreeNode类 
# @return TreeNode类
#
class Solution:def __init__(self):self.prevNode = Nonedef convert2LinkList(self, root):if root == None:returnself.convert2LinkList(root.left)if self.prevNode != None:self.prevNode.right = rootroot.left = self.prevNodeself.prevNode = rootself.convert2LinkList(root.right)def Convert(self , pRootOfTree ):# write code hereif pRootOfTree == None:return Nonehead = pRootOfTreewhile head.left != None:head = head.leftself.convert2LinkList(pRootOfTree)return head