张量的代数操作
张量的性质
张量迹 Tensor Trace
定义 e ^ i ⨂ e ^ j \hat e_i \bigotimes \hat e_j e^i⨂e^j的迹:
T r ( e ^ i ⨂ e ^ j ) = e ^ i ⋅ e ^ j = δ i j Tr(\hat e_i \bigotimes \hat e_j) = \hat e_i \cdot \hat e_j = \delta_{ij} Tr(e^i⨂e^j)=e^i⋅e^j=δij
所以,可以定义二阶张量的迹为:对角线元素加和
T r ( A ) = T r ( A i j e ^ i ⨂ e ^ j ) = A i j T r ( e ^ i ⨂ e ^ j ) = A i j δ i j = A i i Tr(A) = Tr(A_{ij}\hat e_i \bigotimes \hat e_j) = A_{ij}Tr(\hat e_i \bigotimes \hat e_j) = A_{ij}\delta_{ij} = A_{ii} Tr(A)=Tr(Aije^i⨂e^j)=AijTr(e^i⨂e^j)=Aijδij=Aii
并矢的迹为:
T r ( u ⃗ ⨂ v ⃗ ) = u ⃗ i v ⃗ j T r ( e ^ i ⨂ e ^ j ) = u ⃗ i v ⃗ j δ i j = u ⃗ i v ⃗ i = u ⃗ ⋅ v ⃗ Tr(\vec u \bigotimes \vec v) = \vec u_i \vec v_jTr(\hat e_i \bigotimes \hat e_j)= \vec u_i \vec v_j\delta_{ij} = \vec u_i \vec v_i = \vec u \cdot \vec v Tr(u⨂v)=uivjTr(e^i⨂e^j)=uivjδij=uivi=u⋅v
NOTE: 张量的迹是一个不变量,是独立于坐标系的
张量的迹的性质:
- 张量转置的迹等于张量的迹: T r ( A T ) = T r ( A ) Tr(A^T) = Tr(A) Tr(AT)=Tr(A)
- 加法: T r ( A + B ) = T r ( A ) + T r ( B ) Tr(A +B) = Tr(A) + Tr(B) Tr(A+B)=Tr(A)+Tr(B)
- 点积:
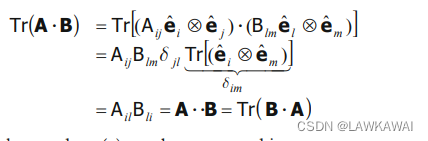
对于另一个双收缩( : ) , 有
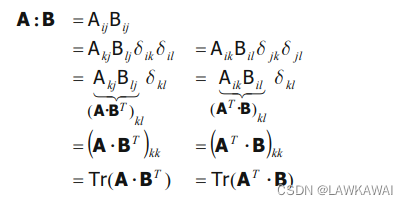
所以, 两个张量进行双收缩( ⋅ ⋅ \cdot \cdot ⋅⋅)操作,等价于求两个张量点积后的迹
两个张量进行双收缩(:)操作,等价于求一个张量与另一个张量转置点积后的迹
同样地,可以验证:
- T r ( A ⋅ B ⋅ C ) = T r ( B ⋅ C ⋅ A ) = T r ( C ⋅ A ⋅ B ) = A i j B j k C k i Tr(A \cdot B \cdot C) = Tr(B \cdot C \cdot A) =Tr(C \cdot A \cdot B) = A_{ij}B_{jk}C_{ki} Tr(A⋅B⋅C)=Tr(B⋅C⋅A)=Tr(C⋅A⋅B)=AijBjkCki
- T r ( A ) = A i i Tr(A) = A_{ii} Tr(A)=Aii
- KaTeX parse error: Expected '}', got 'EOF' at end of input: …A)=A_{ii}A_{jj]
- T r ( A ⋅ A ) = T r ( A 2 ) = A i l A l i Tr(A\cdot A) =Tr(A^2)=A_{il}A_{li} Tr(A⋅A)=Tr(A2)=AilAli
- T r ( A ⋅ A ⋅ A ) = T r ( A 3 ) = A i j A j k A k i Tr(A\cdot A \cdot A)=Tr(A^3) = A_{ij}A_{jk}A_{ki} Tr(A⋅A⋅A)=Tr(A3)=AijAjkAki
问题1.19 证明: ( T m ) T = ( T T ) m (T^m)^T=(T^T)^m (Tm)T=(TT)m 以及 T r ( T T ) m = T r ( T m ) Tr(T^T)^m=Tr(T^m) Tr(TT)m=Tr(Tm)

特殊张量
单位张量:
1 = δ i j e ^ i ⨂ e ^ j = e ^ i ⨂ e ^ i = 1 e ^ i ⨂ e ^ j 1 = \delta_{ij}\hat e_i \bigotimes \hat e_j = \hat e_i \bigotimes \hat e_i = 1 \hat e_i \bigotimes \hat e_j 1=δije^i⨂e^j=e^i⨂e^i=1e^i⨂e^j
四阶单位张量的定义:
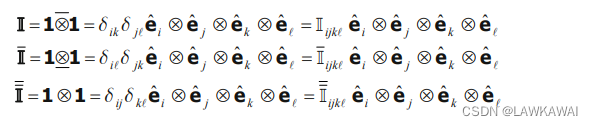
可以计算:
I : A = ( δ i k δ j l e ^ i ⨂ e ^ j ⨂ e ^ k ⨂ e ^ l ) : ( A p q e ^ p ⨂ e ^ q ) = δ i k δ j l A p q δ k p δ l q e ^ i ⨂ e ^ j = δ i k δ j l A k l e ^ i ⨂ e ^ j = A i j e ^ i ⨂ e ^ j = A I:A = (\delta_{ik}\delta_{jl}\hat e_i \bigotimes \hat e_j \bigotimes \hat e_k\bigotimes\hat e_l ): (A_{pq}\hat e_p \bigotimes \hat e_q) \\ =\delta_{ik}\delta_{jl}A_{pq} \delta_{kp} \delta_{lq} \hat e_i \bigotimes \hat e_j \\ =\delta_{ik}\delta_{jl}A_{kl} \hat e_i \bigotimes \hat e_j \\ =A_{ij} \hat e_i \bigotimes \hat e_j \\= A I:A=(δikδjle^i⨂e^j⨂e^k⨂e^l):(Apqe^p⨂e^q)=δikδjlApqδkpδlqe^i⨂e^j=δikδjlAkle^i⨂e^j=Aije^i⨂e^j=A
I ˉ : A = ( δ i l δ j k e ^ i ⨂ e ^ j ⨂ e ^ k ⨂ e ^ l ) : ( A p q e ^ p ⨂ e ^ q ) = δ i l δ j k A p q δ k p δ l q e ^ i ⨂ e ^ j = δ i l δ j k A k l e ^ i ⨂ e ^ j = A j i e ^ i ⨂ e ^ j = A T \bar I:A = (\delta_{il}\delta_{jk}\hat e_i \bigotimes \hat e_j \bigotimes \hat e_k\bigotimes\hat e_l ): (A_{pq}\hat e_p \bigotimes \hat e_q) \\ =\delta_{il}\delta_{jk}A_{pq} \delta_{kp} \delta_{lq} \hat e_i \bigotimes \hat e_j \\ =\delta_{il}\delta_{jk}A_{kl} \hat e_i \bigotimes \hat e_j \\ =A_{ji} \hat e_i \bigotimes \hat e_j \\= A^T Iˉ:A=(δilδjke^i⨂e^j⨂e^k⨂e^l):(Apqe^p⨂e^q)=δilδjkApqδkpδlqe^i⨂e^j=δilδjkAkle^i⨂e^j=Ajie^i⨂e^j=AT
I ‾ ‾ : A = ( δ i j δ k l e ^ i ⨂ e ^ j ⨂ e ^ k ⨂ e ^ l ) : ( A p q e ^ p ⨂ e ^ q ) = δ i j δ k l A p q δ k p δ l q e ^ i ⨂ e ^ j = δ i j δ k l A k l e ^ i ⨂ e ^ j = A k k δ i j e ^ i ⨂ e ^ j = T r ( A ) 1 \overline{\overline{I}} :A = (\delta_{ij}\delta_{kl}\hat e_i \bigotimes \hat e_j \bigotimes \hat e_k\bigotimes\hat e_l ): (A_{pq}\hat e_p \bigotimes \hat e_q) \\ =\delta_{ij}\delta_{kl}A_{pq} \delta_{kp} \delta_{lq} \hat e_i \bigotimes \hat e_j \\ =\delta_{ij}\delta_{kl}A_{kl} \hat e_i \bigotimes \hat e_j \\ =A_{kk}\delta_{ij}\hat e_i \bigotimes \hat e_j \\= Tr(A) 1 I:A=(δijδkle^i⨂e^j⨂e^k⨂e^l):(Apqe^p⨂e^q)=δijδklApqδkpδlqe^i⨂e^j=δijδklAkle^i⨂e^j=Akkδije^i⨂e^j=Tr(A)1
四阶单位张量的对称部分:
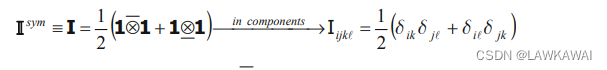
张量乘积符号 ⨂ ‾ \overline{\bigotimes} ⨂ 的定义如下:
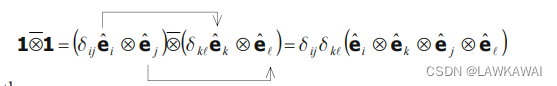
与以下是一样的:
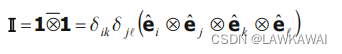
张量乘积符号 ⨂ ‾ \underline{\bigotimes} ⨂ 的定义如下:
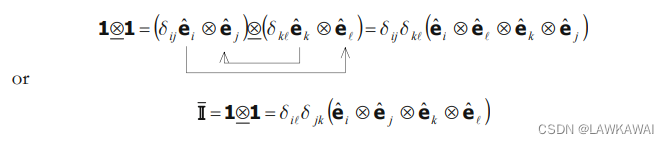
四阶单位张量的反对称部分:

以下等式成立:
b ⃗ ⋅ 1 = b ⃗ \vec b \cdot 1 = \vec b b⋅1=b
I : A = A I:A = A I:A=A
I s y m : A = A s y m I^{sym}:A = A^{sym} Isym:A=Asym
A : 1 = T r ( A ) = A i i A:1 = Tr(A) =A_{ii} A:1=Tr(A)=Aii
A 2 : 1 = T r ( A 2 ) = T r ( A ⋅ A ) = A i l A l i A^2:1 = Tr(A^2)=Tr(A\cdot A) = A_{il}A_{li} A2:1=Tr(A2)=Tr(A⋅A)=AilAli
A 3 : 1 = T r ( A 3 ) = T r ( A ⋅ A ⋅ A ) = A i j A j k A k l A^3:1 = Tr(A^3)=Tr(A\cdot A \cdot A)=A_{ij}A_{jk}A_{kl} A3:1=Tr(A3)=Tr(A⋅A⋅A)=AijAjkAkl
问题1.20 证明: T : 1 = T r ( T ) T:1 = Tr(T) T:1=Tr(T)

Levi-Civita 伪张量(置换张量):
是一个三阶伪张量:
ϵ = ϵ i j k e ^ i ⨂ e ^ j ⨂ e ^ k \epsilon = \epsilon_{ijk} \hat e_i \bigotimes \hat e_j \bigotimes \hat e_k ϵ=ϵijke^i⨂e^j⨂e^k
张量的行列式:
det ( A ) ≡ ∣ A ∣ = ϵ i j k A 1 i A 2 j A 3 k = ϵ i j k A i 1 A j 2 A k 3 \det (A) \equiv|A| = \epsilon_{ijk}A_{1i}A_{2j}A_{3k} = \epsilon_{ijk}A_{i1}A_{j2}A_{k3} det(A)≡∣A∣=ϵijkA1iA2jA3k=ϵijkAi1Aj2Ak3
张量的行列式也是一个不变量(独立于坐标系)
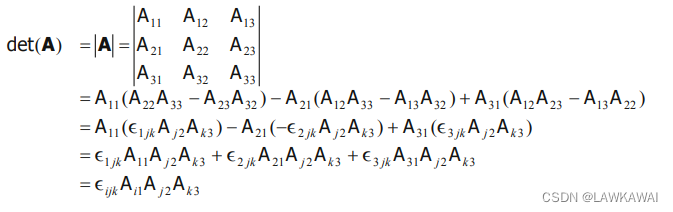
行列式的性质:
det 1 = 1 \det 1 = 1 det1=1
det A T = det A \det A^T = \det A detAT=detA
det ( A ⋅ B ) = det A ⋅ det B \det (A \cdot B) =\det A \cdot \det B det(A⋅B)=detA⋅detB
det ( α A ) = α 3 det A \det (\alpha A) = \alpha^3 \det A det(αA)=α3detA
如果 det A = 0 \det A = 0 detA=0,则A是奇异的
如果交换两行或两列,则行列式的符号改变
如果某一行或某一列的所有元素为0, 则行列式为0
如果对某一行或某一列所有元素乘以c,则行列式变为 c ∣ A ∣ c|A| c∣A∣
如果两行(列)或以上是线性相关的,则行列式为0
问题1.21 证明 ∣ A ∣ ϵ t p q = ϵ r j k A r t A j p A k q |A|\epsilon_{tpq} = \epsilon_{rjk}A_{rt}A_{jp}A_{kq} ∣A∣ϵtpq=ϵrjkArtAjpAkq

以上用到:
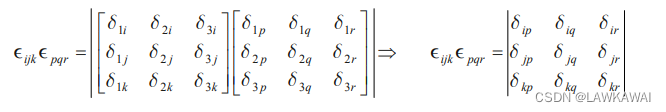
问题1.22 证明: ∣ A ∣ = 1 6 ϵ r j k ϵ t p q A r t A j p A k q |A| = \frac{1}{6}\epsilon_{rjk}\epsilon_{tpq}A_{rt}A_{jp}A_{kq} ∣A∣=61ϵrjkϵtpqArtAjpAkq
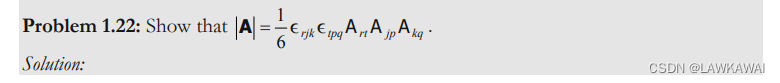

其中用到:
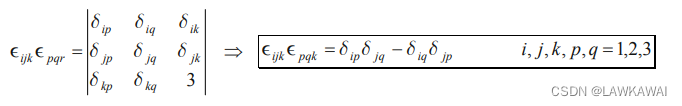
问题1.23 证明: det ( μ 1 + α a ⃗ ⨂ b ⃗ ) = μ 3 + μ 2 α a ⃗ ⋅ b ⃗ \det (\mu 1 + \alpha \vec a \bigotimes \vec b) = \mu^3 + \mu^2 \alpha \vec a \cdot \vec b det(μ1+αa⨂b)=μ3+μ2αa⋅b

由于以下等式也成立:
det [ 1 + α ( a ⃗ ⨂ b ⃗ ) + β ( b ⃗ ⨂ a ⃗ ) ] = 1 + α ( a ⃗ ⋅ b ⃗ ) + β ( a ⃗ ⋅ b ⃗ ) + α β [ ( a ⃗ ⋅ b ⃗ ) 2 − ( a ⃗ ⋅ a ⃗ ) ( b ⃗ ⋅ b ⃗ ) ] \det [1 + \alpha (\vec a \bigotimes \vec b) + \beta (\vec b \bigotimes \vec a)] = 1 + \alpha (\vec a \cdot \vec b) +\beta (\vec a \cdot \vec b) + \alpha \beta [(\vec a \cdot \vec b)^2 - (\vec a \cdot \vec a)(\vec b \cdot \vec b)] det[1+α(a⨂b)+β(b⨂a)]=1+α(a⋅b)+β(a⋅b)+αβ[(a⋅b)2−(a⋅a)(b⋅b)]
令 β = 0 \beta = 0 β=0, 也可以得到 det ( μ 1 + α a ⃗ ⨂ b ⃗ ) = μ 3 + μ 2 α a ⃗ ⋅ b ⃗ \det (\mu 1 + \alpha \vec a \bigotimes \vec b) = \mu^3 + \mu^2 \alpha \vec a \cdot \vec b det(μ1+αa⨂b)=μ3+μ2αa⋅b
如果 α = β \alpha = \beta α=β, 有:
det [ 1 + α ( a ⃗ ⨂ b ⃗ ) + α ( b ⃗ ⨂ a ⃗ ) ] = 1 + α ( a ⃗ ⋅ b ⃗ ) + α ( a ⃗ ⋅ b ⃗ ) + α 2 [ ( a ⃗ ⋅ b ⃗ ) 2 − ( a ⃗ ⋅ a ⃗ ) ( b ⃗ ⋅ b ⃗ ) ] = 1 + α [ 2 ( a ⃗ ⋅ b ⃗ ) − α ( a ⃗ ∧ b ⃗ ) 2 ] \det [1 + \alpha (\vec a \bigotimes \vec b) + \alpha (\vec b \bigotimes \vec a)] \\= 1 + \alpha (\vec a \cdot \vec b) +\alpha (\vec a \cdot \vec b) + \alpha^2 [(\vec a \cdot \vec b)^2 - (\vec a \cdot \vec a)(\vec b \cdot \vec b)] \\ = 1 + \alpha [2(\vec a \cdot \vec b) - \alpha (\vec a \wedge \vec b)^2] det[1+α(a⨂b)+α(b⨂a)]=1+α(a⋅b)+α(a⋅b)+α2[(a⋅b)2−(a⋅a)(b⋅b)]=1+α[2(a⋅b)−α(a∧b)2]
其中,用到:
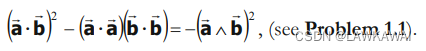
以下等式成立:
det ( α A + β B ) = α 3 det A + α 2 β T r ( B ⋅ a d j ( A ) ) + α β 2 [ A ⋅ a d j ( B ) ] + β 3 det B \det (\alpha A + \beta B) \\ =\alpha^3\det A + \alpha^2 \beta Tr(B \cdot adj(A))+ \alpha \beta^2 [A \cdot adj(B)] + \beta^3 \det B det(αA+βB)=α3detA+α2βTr(B⋅adj(A))+αβ2[A⋅adj(B)]+β3detB
当 α = 1 , A = 1 , B = a ⃗ ⨂ b ⃗ \alpha = 1, A = 1, B = \vec a \bigotimes \vec b α=1,A=1,B=a⨂b, 且由于 det ( a ⃗ ⨂ b ⃗ ) = 0 \det (\vec a \bigotimes \vec b) = 0 det(a⨂b)=0 以及 c o f ( a ⃗ ⨂ b ⃗ ) = 0 cof(\vec a \bigotimes \vec b) = 0 cof(a⨂b)=0, 有
det ( 1 + β a ⃗ ⨂ b ⃗ ) = det 1 + β T r [ a ⃗ ⨂ b ⃗ ⋅ 1 ] = 1 + β T r [ a i b j ] = 1 + β a ⃗ ⋅ b ⃗ \det (1 + \beta \vec a \bigotimes \vec b) = \det 1 + \beta Tr[\vec a \bigotimes \vec b \cdot 1] = 1+\beta Tr[a_ib_j] = 1+ \beta \vec a \cdot \vec b det(1+βa⨂b)=det1+βTr[a⨂b⋅1]=1+βTr[aibj]=1+βa⋅b
性质:
( A ⋅ a ⃗ ) ⋅ [ ( A ⋅ b ⃗ ) ∧ ( A ⋅ c ⃗ ) ] = det ( A ) [ a ⃗ ⋅ b ⃗ ∧ c ⃗ ] \boxed{(A \cdot \vec a) \cdot [(A \cdot \vec b) \wedge (A \cdot \vec c)] = \det (A)[\vec a \cdot \vec b \wedge \vec c]} (A⋅a)⋅[(A⋅b)∧(A⋅c)]=det(A)[a⋅b∧c]
证明:
由于 a ⃗ ⋅ ( b ⃗ ∧ c ⃗ ) = ϵ i j k a i b j c k \vec a \cdot (\vec b \wedge \vec c) = \epsilon_{ijk} a_i b_j c_k a⋅(b∧c)=ϵijkaibjck
两边同乘 ∣ A ∣ |A| ∣A∣:
a ⃗ ⋅ ( b ⃗ ∧ c ⃗ ) ∣ A ∣ = ϵ i j k a i b j c k ∣ A ∣ \vec a \cdot (\vec b \wedge \vec c) |A| = \epsilon_{ijk} a_i b_j c_k |A| a⋅(b∧c)∣A∣=ϵijkaibjck∣A∣
又由于 ∣ A ∣ ϵ i j k = ϵ p q r A p i A q j A r k |A|\epsilon_{ijk} = \epsilon_{pqr} A_{pi}A_{qj}A_{rk} ∣A∣ϵijk=ϵpqrApiAqjArk, 因此:
a ⃗ ⋅ ( b ⃗ ∧ c ⃗ ) ∣ A ∣ = ϵ i j k a i b j c k ∣ A ∣ = ϵ p q r A p i A q j A r k a i b j c k = ϵ p q r A p i a i A q j b j A r k c k = ( A ⋅ a ⃗ ) ⋅ [ ( A ⋅ b ⃗ ) ∧ ( A ⋅ c ⃗ ) ] = [ ( A ⋅ b ⃗ ) ∧ ( A ⋅ c ⃗ ) ] ⋅ ( A ⋅ a ⃗ ) \vec a \cdot (\vec b \wedge \vec c) |A| = \epsilon_{ijk} a_i b_j c_k |A| \\=\epsilon_{pqr} A_{pi}A_{qj}A_{rk} a_i b_j c_k \\=\epsilon_{pqr} A_{pi}a_iA_{qj}b_jA_{rk}c_k \\ =(A \cdot \vec a) \cdot [(A \cdot \vec b) \wedge (A \cdot \vec c)] \\= [(A \cdot \vec b) \wedge (A \cdot \vec c)]\cdot (A \cdot \vec a) a⋅(b∧c)∣A∣=ϵijkaibjck∣A∣=ϵpqrApiAqjArkaibjck=ϵpqrApiaiAqjbjArkck=(A⋅a)⋅[(A⋅b)∧(A⋅c)]=[(A⋅b)∧(A⋅c)]⋅(A⋅a)
张量的逆
张量的逆: A − 1 A^{-1} A−1
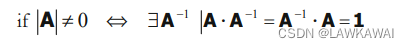
指标形式:
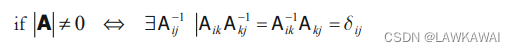
为了计算张量的逆,我们从伴随张量(Adjugate Tensor)开始:
a d j ( A T ) ⋅ ( a ⃗ ∧ b ⃗ ) = ( A ⋅ a ⃗ ) ∧ ( A ⋅ b ⃗ ) adj(A^T)\cdot (\vec a \wedge \vec b)=(A \cdot \vec a)\wedge (A \cdot \vec b) adj(AT)⋅(a∧b)=(A⋅a)∧(A⋅b)
两边同乘以一个任意的向量 d ⃗ \vec d d
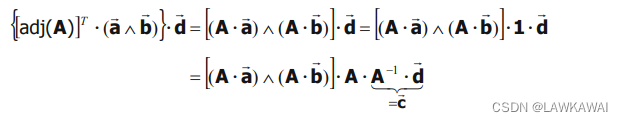
上一节,证明了:
a ⃗ ⋅ ( b ⃗ ∧ c ⃗ ) ∣ A ∣ = [ ( A ⋅ b ⃗ ) ∧ ( A ⋅ c ⃗ ) ] ⋅ ( A ⋅ a ⃗ ) \vec a \cdot (\vec b \wedge \vec c) |A| = [(A \cdot \vec b) \wedge (A \cdot \vec c)]\cdot (A \cdot \vec a) a⋅(b∧c)∣A∣=[(A⋅b)∧(A⋅c)]⋅(A⋅a)
所以有:
c ⃗ ⋅ ( a ⃗ ∧ b ⃗ ) ∣ A ∣ = [ ( A ⋅ a ⃗ ) ∧ ( A ⋅ b ⃗ ) ] ⋅ ( A ⋅ c ⃗ ) \vec c \cdot (\vec a \wedge \vec b) |A| = [(A \cdot \vec a) \wedge (A \cdot \vec b)]\cdot (A \cdot \vec c) c⋅(a∧b)∣A∣=[(A⋅a)∧(A⋅b)]⋅(A⋅c)
因此:
[ ( a d j ( A ) ) T ⋅ ( a ⃗ ∧ b ⃗ ) ] ⋅ d ⃗ = [ ( A ⋅ a ⃗ ) ∧ ( A ⋅ b ⃗ ) ] ⋅ ( A ⋅ A − 1 ⋅ d ⃗ ) = A − 1 ⋅ d ⃗ ⋅ ( a ⃗ ∧ b ⃗ ) ∣ A ∣ = ∣ A ∣ ( a ⃗ ∧ b ⃗ ) ⋅ A − 1 ⋅ d ⃗ [ (adj(A))^T\cdot (\vec a \wedge \vec b) ] \cdot \vec d =[(A \cdot \vec a) \wedge (A \cdot \vec b)]\cdot (A \cdot A^{-1} \cdot \vec d) \\=A^{-1} \cdot \vec d \cdot (\vec a \wedge \vec b) |A| \\ =|A| (\vec a \wedge \vec b)\cdot A^{-1} \cdot \vec d [(adj(A))T⋅(a∧b)]⋅d=[(A⋅a)∧(A⋅b)]⋅(A⋅A−1⋅d)=A−1⋅d⋅(a∧b)∣A∣=∣A∣(a∧b)⋅A−1⋅d
令 p ⃗ = a ⃗ ∧ b ⃗ \vec p = \vec a \wedge \vec b p=a∧b, 上式可以重写为:
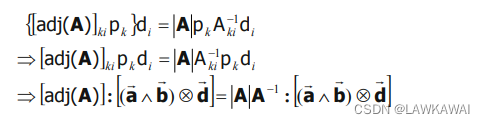
因此: [ a d j ( A ) ] = ∣ A ∣ A − 1 [adj(A)] = |A| A^{-1} [adj(A)]=∣A∣A−1
所以, 张量的逆, A − 1 = 1 ∣ A ∣ [ a d j ( A ) ] = 1 ∣ A ∣ [ c o f ( A ) ] T \boxed{A^{-1} = \frac{1}{|A|}[adj(A)] = \frac{1}{|A|}[cof(A)]^T} A−1=∣A∣1[adj(A)]=∣A∣1[cof(A)]T
可逆张量,有以下性质:
( A ⋅ B ) − 1 = B − 1 ⋅ A − 1 (A \cdot B)^{-1} = B^{-1} \cdot A^{-1} (A⋅B)−1=B−1⋅A−1
( A − 1 ) − 1 = A (A^{-1})^{-1} = A (A−1)−1=A
( β A ) − 1 = 1 β A − 1 (\beta A)^{-1} = \frac{1}{\beta}A^{-1} (βA)−1=β1A−1
det ( A − 1 = [ det A ] − 1 ) \det (A^{-1} = [\det A]^{-1}) det(A−1=[detA]−1)
可逆转置:
A − T ≡ ( A − 1 ) T ≡ ( A T ) − 1 A^{-T} \equiv (A^{-1})^T \equiv (A^T)^{-1} A−T≡(A−1)T≡(AT)−1
证明 a d j ( A ⋅ B ) = a d j ( A ) ⋅ a d j ( B ) adj(A \cdot B) = adj(A) \cdot adj(B) adj(A⋅B)=adj(A)⋅adj(B):
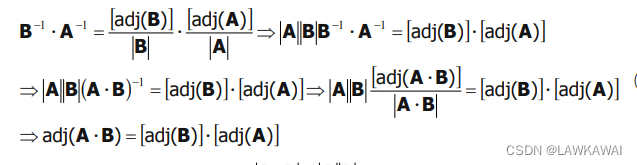
其中,用到了性质: ∣ A ⋅ B ∣ = ∣ A ∣ ∣ B ∣ |A \cdot B| = |A| |B| ∣A⋅B∣=∣A∣∣B∣
同样的, 可以证明: c o f ( A ⋅ B ) = [ c o f ( A ) ] ⋅ [ c o f ( B ) ] cof(A \cdot B) = [cof(A)] \cdot [cof(B)] cof(A⋅B)=[cof(A)]⋅[cof(B)]
计算矩阵A的逆的步骤:
-
计算矩阵的余子式: cof(A)
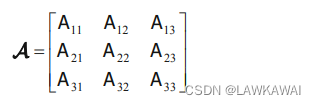
定义一个矩阵M, 其元素 M i j M_{ij} Mij为矩阵A消去第i行第j列之后的行列式:

所以,定义矩阵A的余子式为:
c o f ( A ) = ( − 1 ) i + j M i j cof (A) = (-1)^{i+j}M_{ij} cof(A)=(−1)i+jMij -
计算伴随矩阵, adj(A),
a d j ( A ) = [ c o f ( A ) ] T adj(A) = [cof(A)]^T adj(A)=[cof(A)]T -
计算矩阵的逆:
A − 1 = a d j ( A ) ∣ A ∣ A^{-1} = \frac{adj(A)}{|A|} A−1=∣A∣adj(A)
由于:
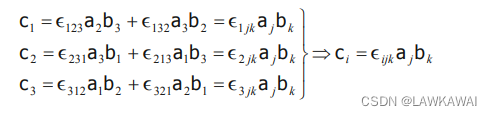
可以将矩阵的余子式的每一行写成:
M 1 i = ϵ i j k A 2 j A 3 k M_{1i} = \epsilon_{ijk}A_{2j}A_{3k} M1i=ϵijkA2jA3k
M 2 i = ϵ i j k A 1 j A 3 k M_{2i} = \epsilon_{ijk}A_{1j}A_{3k} M2i=ϵijkA1jA3k
M 3 i = ϵ i j k A 1 j A 2 k M_{3i} = \epsilon_{ijk}A_{1j}A_{2k} M3i=ϵijkA1jA2k
问题1.24 证明:当且仅当 det A = 0 \det A = 0 detA=0, 存在非零向量 n ⃗ ≠ 0 ⃗ \vec n \neq \vec 0 n=0使得 A ⋅ n ⃗ = 0 ⃗ A\cdot \vec n = \vec 0 A⋅n=0


正交张量
在连续介质力学,正交张量发挥了很重要的角色
若二阶张量 Q Q Q满足其转置与其逆相等: Q T = Q − 1 Q^T = Q^{-1} QT=Q−1,则称 Q Q Q 是正交张量
Q ⋅ Q T = Q T ⋅ Q = 1 Q \cdot Q^T = Q^T \cdot Q = 1 Q⋅QT=QT⋅Q=1
Q i k Q j k = Q k i Q k j = δ i j Q_{ik}Q_{jk} = Q_{ki}Q_{kj}= \delta_{ij} QikQjk=QkiQkj=δij
性质:
- Q的逆等于Q的转置,正交性: Q − 1 = Q T Q^{-1}=Q^T Q−1=QT
- Q是旋转张量, 如果: det Q ≡ ∣ Q ∣ = + 1 \det Q \equiv |Q| = +1 detQ≡∣Q∣=+1
如果 ∣ Q ∣ = − 1 |Q| = -1 ∣Q∣=−1正交张量为反射张量
两个正交张量点积得到的张量也是正交的:
C − 1 = ( A ⋅ B ) − 1 = B − 1 ⋅ A − 1 = B T ⋅ A T = ( A ⋅ B ) T = C T C^{-1} = (A \cdot B)^{-1}= B^{-1} \cdot A^{-1} = B^T \cdot A^T= (A\cdot B)^T=C^T C−1=(A⋅B)−1=B−1⋅A−1=BT⋅AT=(A⋅B)T=CT
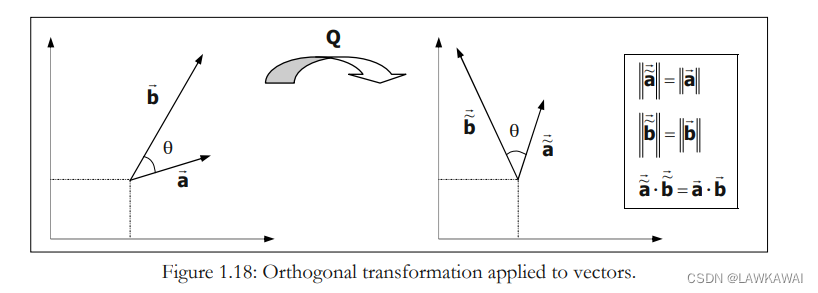
正交变换:
a ~ ⃗ = Q ⋅ a ⃗ \vec{\tilde a}=Q \cdot \vec a a~=Q⋅a
b ~ ⃗ = Q ⋅ b ⃗ \vec{\tilde b}=Q \cdot \vec b b~=Q⋅b
以上向量点积:
a ~ ⃗ ⋅ b ~ ⃗ = ( Q ⋅ a ⃗ ) ⋅ ( Q ⋅ b ⃗ ) = a ⃗ ⋅ Q T ⋅ Q ⋅ b ⃗ = a ⃗ ⋅ 1 ⋅ b ⃗ = a ⃗ ⋅ b ⃗ \vec{\tilde a} \cdot \vec{\tilde b}=(Q \cdot \vec a) \cdot (Q \cdot \vec b)=\vec a\cdot Q^T\cdot Q\cdot \vec b=\vec a\cdot1\cdot \vec b = \vec a \cdot \vec b a~⋅b~=(Q⋅a)⋅(Q⋅b)=a⋅QT⋅Q⋅b=a⋅1⋅b=a⋅b
a ~ i b ~ i = ( Q i k a k ) ( Q i j b j ) = a k ( Q i k Q i j ) b j = a k δ k j b j = a k b k \tilde a_i \tilde b_i=(Q_{ik}a_k) (Q_{ij}b_j)=a_k(Q_{ik}Q_{ij})b_j=a_k\delta_{kj}b_j=a_kb_k a~ib~i=(Qikak)(Qijbj)=ak(QikQij)bj=akδkjbj=akbk
同样的,对于 a ~ ⃗ = b ~ ⃗ \vec{\tilde a} = \vec{\tilde b} a~=b~,,有: a ~ ⃗ ⋅ a ~ ⃗ = ∣ ∣ a ~ ⃗ ∣ ∣ 2 = a ⃗ ⋅ a ⃗ = ∣ ∣ a ⃗ ∣ ∣ 2 \vec{\tilde a} \cdot \vec{\tilde a}=||\vec{\tilde a}||^2=\vec a \cdot \vec a=||\vec a||^2 a~⋅a~=∣∣a~∣∣2=a⋅a=∣∣a∣∣2
因此,在一个正交变换中,向量的大小和它们之间的角度不会改变。
正定张量、负定张量和半正定张量
正定的 positive definite: 对于所有 x ^ ≠ 0 ⃗ \hat x \neq \vec 0 x^=0
张量表示: x ^ ⋅ T ⋅ x ^ > 0 \hat x \cdot T \cdot \hat x >0 x^⋅T⋅x^>0
指标表示: x i T i j x j > 0 x_i T_{ij}x_j > 0 xiTijxj>0
负定的 negative definite: 对于所有 x ^ ≠ 0 ⃗ \hat x \neq \vec 0 x^=0
张量表示: x ^ ⋅ T ⋅ x ^ < 0 \hat x \cdot T \cdot \hat x <0 x^⋅T⋅x^<0
指标表示: x i T i j x j < 0 x_i T_{ij}x_j < 0 xiTijxj<0
半正定的 semi-positive definite: 对于所有 x ^ ≠ 0 ⃗ \hat x \neq \vec 0 x^=0
张量表示: x ^ ⋅ T ⋅ x ^ ≥ 0 \hat x \cdot T \cdot \hat x \geq 0 x^⋅T⋅x^≥0
指标表示: x i T i j x j ≥ 0 x_i T_{ij}x_j \geq 0 xiTijxj≥0
负定的 negative definite: 对于所有 x ^ ≠ 0 ⃗ \hat x \neq \vec 0 x^=0
张量表示: x ^ ⋅ T ⋅ x ^ ≤ 0 \hat x \cdot T \cdot \hat x \leq 0 x^⋅T⋅x^≤0
指标表示: x i T i j x j ≤ 0 x_i T_{ij}x_j \leq 0 xiTijxj≤0
若 α = x ^ ⋅ T ⋅ x ^ = T : ( x ^ ⨂ x ^ ) = T i j x i x j \alpha =\hat x \cdot T \cdot \hat x = T:(\hat x \bigotimes \hat x) = T_{ij}x_ix_j α=x^⋅T⋅x^=T:(x^⨂x^)=Tijxixj,则 α \alpha α关于 x ^ \hat x x^的导数为:
∂ α ∂ x k = T i j ∂ x i ∂ x k x j + T i j x i ∂ x j ∂ x k = T i j δ i k x j + T i j x i δ j k = T k j x j + T i k x j = ( T k i + T i k ) x i \frac{\partial \alpha}{\partial x_k} = T_{ij}\frac{\partial x_i}{\partial x_k}x_j+T_{ij}x_i\frac{\partial x_j}{\partial x_k}\\= T_{ij}\delta_{ik}x_j+T_{ij}x_i\delta_{jk} \\ =T_{kj}x_j+T_{ik}x_j \\ =(T_{ki}+T_{ik})x_i ∂xk∂α=Tij∂xk∂xixj+Tijxi∂xk∂xj=Tijδikxj+Tijxiδjk=Tkjxj+Tikxj=(Tki+Tik)xi
所以:
∂ α ∂ x ^ = 2 T s y m ⋅ x ^ ⟹ ∂ 2 α ∂ x ^ ⨂ ∂ x ^ = 2 T s y m \frac{\partial \alpha}{\partial \hat x}=2T^{sym}\cdot \hat x \implies \frac{\partial^2\alpha}{\partial \hat x \bigotimes \partial \hat x} = 2T^{sym} ∂x^∂α=2Tsym⋅x^⟹∂x^⨂∂x^∂2α=2Tsym
同样的,以下等式成立:
x ^ ⋅ T ⋅ x ^ = x ^ ⋅ T s y m ⋅ x ^ \hat x \cdot T \cdot \hat x = \hat x \cdot T^{sym} \cdot \hat x x^⋅T⋅x^=x^⋅Tsym⋅x^
因为如果张量的对称部分是正定的,那么该张量也是正定的
NOTE: T的特征值必须为正,T才能为正定的
问题1.25 证明: C = F T ⋅ F C = F^T \cdot F C=FT⋅F和 b = F ⋅ F T b = F \cdot F^T b=F⋅FT都是对称半正定张量。并确定什么条件下 C 和 b C和b C和b是正定张量


张量的加性分解
任意两个张量 S , T ≠ 0 S, T\neq 0 S,T=0,将 S S S表示成张量的加性分解:
S = α T + U ,其中 U = S − α T S = \alpha T + U, 其中 U = S - \alpha T S=αT+U,其中U=S−αT
所以, S S S由 α \alpha α决定,有无穷多种分解方式
然而,当 T r ( T ⋅ U T ) = T r ( U ⋅ T T ) = 0 Tr(T \cdot U^T) = Tr(U \cdot T^T)=0 Tr(T⋅UT)=Tr(U⋅TT)=0, 则加性分解是唯一的
S ⋅ T T = α T ⋅ T T + U ⋅ T T ⟹ T r ( S ⋅ T T ) = α T r ( T ⋅ T T ) + T r ( U ⋅ T T ) = α T r ( T ⋅ T T ) S\cdot T^T =\alpha T \cdot T^T+U\cdot T^T \\ \implies Tr(S\cdot T^T ) = \alpha Tr(T \cdot T^T) +Tr(U \cdot T^T)=\alpha Tr(T\cdot T^T) S⋅TT=αT⋅TT+U⋅TT⟹Tr(S⋅TT)=αTr(T⋅TT)+Tr(U⋅TT)=αTr(T⋅TT)
⟹ α = T r ( S ⋅ T T ) T r ( T ⋅ T T ) \implies\alpha = \frac{Tr(S\cdot T^T ) }{Tr(T\cdot T^T)} ⟹α=Tr(T⋅TT)Tr(S⋅TT)
假设 T = 1 T = 1 T=1
α = T r ( S ⋅ 1 ) T r ( 1 ⋅ 1 ) = T r ( S ) T r ( 1 ) = T r ( S ) 3 \alpha = \frac{Tr(S\cdot 1 ) }{Tr(1\cdot 1)} =\frac{Tr(S ) }{Tr(1)} = \frac{Tr(S ) }{3} α=Tr(1⋅1)Tr(S⋅1)=Tr(1)Tr(S)=3Tr(S)
U = S − α T = S − T r ( S ) 3 1 ≡ S d e v U = S - \alpha T=S - \frac{Tr(S ) }{3} 1 \equiv S^{dev} U=S−αT=S−3Tr(S)1≡Sdev
所以:
S = T r ( S ) 3 1 + S d e v = S s p h + S d e v S = \frac{Tr(S ) }{3} 1 + S^{dev} =S^{sph} + S^{dev} S=3Tr(S)1+Sdev=Ssph+Sdev
NOTE:
S s p h = T r ( S ) 3 1 S^{sph} = \frac{Tr(S ) }{3} 1 Ssph=3Tr(S)1是球形张量;
S d e v = S − T r ( S ) 3 1 S^{dev} = S - \frac{Tr(S ) }{3} 1 Sdev=S−3Tr(S)1是偏张量
如果 T = 1 2 ( S + S T ) T = \frac{1}{2}(S + S^T) T=21(S+ST),则
α = = T r ( S ⋅ T T ) T r ( T ⋅ T T ) = 1 2 T r ( S ⋅ ( S + S T ) T ) 1 4 T r ( ( S + S T ) ⋅ ( S + S T ) T ) = 1 \alpha = \frac{}{} = \frac{Tr(S\cdot T^T ) }{Tr(T\cdot T^T)} = \frac{\frac{1}{2}Tr(S\cdot (S + S^T)^T ) }{\frac{1}{4}Tr((S + S^T)\cdot (S + S^T)^T)}=1 α==Tr(T⋅TT)Tr(S⋅TT)=41Tr((S+ST)⋅(S+ST)T)21Tr(S⋅(S+ST)T)=1
可以定义 U = S − α T = S − T = S − 1 2 ( S + S T ) = 1 2 ( S − S T ) U = S - \alpha T=S-T=S-\frac{1}{2}(S + S^T)=\frac{1}{2}(S-S^T) U=S−αT=S−T=S−21(S+ST)=21(S−ST)
所以可以得到 S S S的加性分解为:
S = 1 2 ( S + S T ) + 1 2 ( S − S T ) = S s y m + S s k e w S = \frac{1}{2}(S + S^T)+\frac{1}{2}(S - S^T) = S^{sym} + S^{skew} S=21(S+ST)+21(S−ST)=Ssym+Sskew
问题1.26 求四阶张量 P P P使得 P : A = A d e v P:A=A^{dev} P:A=Adev,其中 A A A是二阶张量

其中,用到:
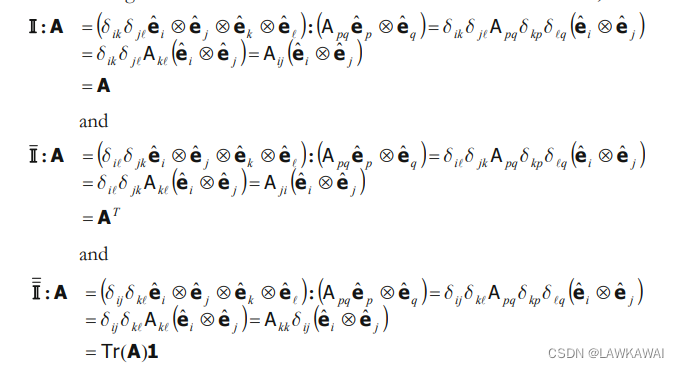
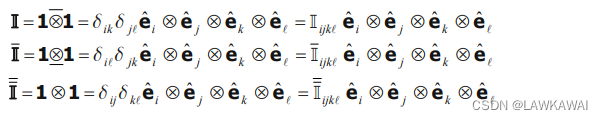
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics