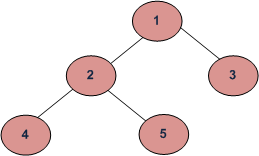
用数学归纳法证明二叉树的先序遍历序列和中序遍历序列可以唯一确定一颗二叉树。
首先说明：思想来自文都考研洪老师。包括逻辑框架的搭建，此篇文章为框架搭建完成后将细节补充完整。

首先，用到的数学的证明思想是第二类数学归纳法（完整归纳法），
其思想如下：
（1）第二类数学归纳法（完整归纳法）
1.当n=1时，形式成立（数学形式）。
2.当n<=k时，假设形式成立。
3.当n=k+1时，形式成立。
那么可以得出结论，这个数学形式可以在n等于任意自然数时，都可以使得形式成立。

给定一颗二叉树（树非空，结点个数为n）
1.当n=1时， 树的先序遍历序列为（a）
树的中序遍历序列为（a）
那么可以唯一确定一颗二叉树 a
2.假设n<=k时，
一颗树的先序遍历序列和中序遍历序列可以唯一确定一颗二叉树。
3.当n=k+1时
先序遍历序列（A1,A2,A3,A4,…,Am）
中序遍历序列（B1,B2,B3,B4,…,Bm）

a.当A1=B1时，即先序遍历的第一个遍历结点（为树的根结点）等于中序遍历的第一个结点的时候，说明中序遍历B1（B1为根结点）之前无左子树，（中序遍历若要先遍历根结点要先中序遍历左子树，若B1之前为空，说明没有中序遍历左子树，说明B1的左子树为空）
{
因为中序遍历的递归定义是
1.中序遍历左子树，
2.遍历根节点，
3.中序遍历右子树。
}
故而又说明中序遍历序列B1之后的结点即（B2,B3,B4,…,Bm）为B1的右子树
又因为m=n=k+1
所以（B2,B3,B4,…,Bm）共有m-2+1=m-1=k+1-1=k个结点。
而先序遍历序列A1之后的序列（A2,A3,A4,…,Am）
也有m-1=k+1-1=k个结点。
这时候符合假设，当n<=k时，的结论，所以根据数学归纳法，可以证明在这种情况下，一棵树的先序遍历序列和中序遍历序列可以唯一确定一颗二叉树。

b.
先序遍历序列（A1,A2,A3,A4,…,Am）
中序遍历序列（B1,B2,B3,B4,…,Bm）
当A1=Bm时，Bm无右子树，同3.a的证明思路一样，可以证明在这种情况下，一棵树的先序遍历序列和中序遍历序列可以唯一确定一颗二叉树。
c.（已经证明了A1=B1或者A1=Bm的情况，现在要证明的是A1=（B2,B3,B4,…,Bm-1）中任意一个的情况时，一棵树的先序遍历序列和中序遍历序列可以唯一确定一颗二叉树）
先序遍历序列（A1,A2,A3,A4,…,Am）
中序遍历序列（B1,B2,B3,B4,…,Bm）
当先序遍历序列（A1,A2,A3,A4,…,Am）中的A1为中序序列中的
（B2,B3,B4,…,Bm-1）时

设A1=Bj，那么这棵树的中序遍历序列为
{(B1,B2,B3,…,Bj-1)Bj (Bj+1,Bj+2,Bj+3,…,Bm )}
而因为（B1,B2,B3,B4,…,Bm）为中序遍历序列所以
Bj的左子树为(B1,B2,B3,…,Bj-1)
Bj的右子树为(Bj+1,Bj+2,Bj+3,…,Bm )
设Bj的左子树的结点个数为x个，Bj的右子树的结点个数为y个，
那么可以明确的是，
1<=x<=m-1-1(由c的条件可得，Bj不能为Bm，由c的条件可得，所以Bj的右子树最小为1个结点，而Bj本身又是一个结点，所以Bj左子树结点的个数最大为m-1-1，即总的减去Bj再减去Bj右子树最小的时候，就是Bj左子树最大的时候)
而确定y也是同理，只不过成立确定Bj右子树的结点个数的范围。
1<=y<=m-1-1
而且，x+y=m-1
(Bj的左右子树的总个数即为总的个数减去Bj本身)。

而这个时候，
Bj的左子树为(B1,B2,B3,…,Bj-1)
节点个数1<=x<=m-1-1=k-1 (m=n=k+1)
Bj的右子树为(Bj+1,Bj+2,Bj+3,…,Bm )
结点个数1<=y<=m-1-1=k-1 (m=n=k+1)
由于A1=Bj 先序遍历序列（A1,A2,A3,A4,…,Am）

又因为先序遍历的递归定义为{
遍历根节点，
先序遍历根节点的左子树，
先序遍历根节点的右子树。
}
所以先序遍历序列为（A1,A2,A3,A4,…,Am）
逻辑上为
（A1,（A1的左子树的先序遍历），（A1的右子树的先序遍历））。

又因为中序遍历的递归定义是
1.中序遍历左子树，
2.遍历根节点，
3.中序遍历右子树。

而此树的中序遍历序列为（B1,B2,B3,B4,…,Bm）
所以中序遍历序列的逻辑上为
（（Bj左子树的中序遍历序列），Bj，（Bj的右子树的中序遍历序列））

从而可以得到，
（A1,（A1的左子树的先序遍历），（A1的右子树的先序遍历））
（（Bj左子树的中序遍历序列），Bj，（Bj的右子树的中序遍历序列））

从而又得到
（A1的左子树的先序遍历序列）
（Bj的左子树的中序遍历序列）
和
（A1的右子树的先序遍历序列）
（Bj的右子树的中序遍历序列）

而且A1=Bj（此表达式说明A1、Bj标识的是树中的同一个结点）
所以得到的是同一个节点的
（Bj（或A1）的左子树的先序遍历序列）|Bj（或A1）的左子树结点
（Bj（或A1）的左子树的中序遍历序列）|个数1<=x<=m-1-1=k-1
和
（Bj（或A1）的右子树的先序遍历序列）|Bj（或A1）的右子树结点
（Bj（或A1）的右子树的中序遍历序列）|个数为1<=y<=m-1-1=k-1

所以，就将规模为n=m=k+1的问题化为了两个问题规模为
1<=n<=m-1-1=k-1的问题
又因为假设n<=k时，数学结论成立，
所以问题规模为k+1的问题化为了
两个问题规模为1<=n<=m-1-1=k-1的时候
{（（唯一左子树），根，（唯一右子树））=唯一二叉树}，
问题规模为k+1的数学结论也成立 。
从而推出n=k+1时数学结论成立。

根据第二类数学归纳法（完整归纳法）
1.因为n=1时数学结论成立，

2.而且n<=k时，假设数学结论是成立的，

3.还有可以将问题规模为k+1的问题化为两个问题规模为1<=n<=k-1的子问题，（因为假设n<=k时数学结论成立）从而推出n=k+1时数学结论成立{（（唯一左子树），根，（唯一右子树））=唯一二叉树}，

从而可以推出，当n为任何自然数时，数学结论都成立，所以，当n取任意自然数时，结点个数为n先序遍历序列和中序遍历序列可以唯一确定一个结点个数为n的二叉树

证毕。（同样的思路可以证明结点个数为n的后序遍历序列和结点个数为n中序遍历序列可以唯一确定一颗结点个数为n二叉树）

注： 1。数学归纳法只是验证经验模型或者经验式子是否足以成为规律，它并不是演绎推理得出数学规律的手段，而是验证手段
2。当n=k+1时不能直接代入n<=k的式子，而是要从n<=k的式子推出n=k+1的式子的形式与n<k+1的一样，这样才是数学归纳
3。证明的突破口在先序遍历二叉树和中序遍历二叉树的定义
注意 根节点是同一个根节点，因为同一颗二叉树只有一个根节点
根的左子树也是相同的，根的右子树也是相同的
{根节点 先序遍历左子树 先序遍历右子树}
{中序遍历右子树 根节点 中序遍历右子树}