这是前段时间做的一个课程设计,做的比较简单,没有考虑到太细,只是初步地达到了想要的效果。这次设计主要是对心电信号进行预处理,将其信号中包含的一些干扰滤除或者抑制掉。
一、心电信号
(1)心电信号的特性
①工频干扰②基线漂移③肌电干扰
心电信号具有以下几个特点:
·信号极其微弱,一般只有0.05~4mV,典型值为1mV;
·频率范围较低,频率范围为0.1~35Hz,主要集中在5~20Hz;
·存在不稳定性。人体内部各器官问的相互影响以及各人的心脏位置、呼吸、年龄、是否经常锻炼等因素,都会使心电信号发生相应变化;
·干扰噪声很强。对心电信号进行测量时,必然要与外界联系,但由于其自身的信号非常微弱,因此,各种干扰噪声非常容易影响测量。
其噪声可能来自工频(50Hz)干扰、电极接触噪点、运动伪迹、肌电噪声、呼吸引起的基线漂移和心电幅度变化以及其他电子设备的机器噪声等诸多方面。
(2)心电信号的选择
本次实验所采用的心电信号来自MIT-BIH库(心律失常数据库,关于这个库的介绍可以参考:点击打开链接),库中有48组失常的心电信号,要在其中找出符合实验要求的心电信号(即含有肌电干扰、工频干扰和基线漂移)。
(3)正常心电信号波形
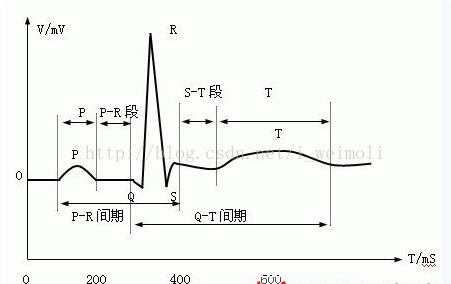
图1 正常心电信号波形
图1是正常心电信号在一个周期内的波形,由P波、QRS波群和T波组成。
P波是由心房的去极化产生的,其波形比较小,形状有些圆,幅度约为0.25mV,持续时间为0.08~0.11s。窦房结去极化发生在心房肌细胞去极化之前,因而在时间上要先于P波,只是窦房结处于心脏内部,其电活动在体表难以采集。
P-R间期是指P波起点和QRS波群起点所跨越的时间,是窦房结产生的兴奋,经过右心房、左心房、房室交接区、房室束、左右束支之后,传到到心室所需要的时间。在正常的体表心电图中,P-R间期的值为0.12~0.2s,其中大部分时间是兴奋在房室交界区内传导所需要的时间。P-R间期也称为房室传导时间。
P-R段是指P波终点和QRS波群起点之间所跨越的时间。在正常的体表心电图中,P-R段的心电信号电位值都是接近基线水平的很小点位。在P-R段期间,左右心房同时兴奋,因而两者产生的综合电场对体表心电图的影响较小。另外,此时的兴奋还处于房室交界区和房室束特殊传导系统中,没有到达心室,因而没有产生较大波动的体表心电图信号。
QRS波群是左右心室肌细胞一次发生去极化所产生的膜外负电位在体表的反应。QRS波群的持续时间为0.06~0.1s。由于心室肌细胞在兴奋过程中的综合电场向量多次发生改变,因而形成了体表心电图中大小和方向多次发生变化的心电信号,其中QRS波群中第一个向下的波为Q波,第一个向上的波为R波,R波后面的为S波。
S-T段是指QRS波群终点和T波起点之间所跨越的时间。S-T段期间,左右心室的肌细胞都处于兴奋期间,因而两者形成的综合电场向量在体表心电图中的贡献非常小,导致S-T段心电信号处于大约基线的水平。
T波由心室肌细胞的复极化产生,其幅度为0.1~0.8mV,持续时间为0.05~0.25s。由于复极化差异的存在,T波的方向和QRS波群主波的方向一致。在R波向上的情况下,T波的幅度一般都超过R波幅度的1/10。Q-T间期是指QRS波群起点和T波终点所跨越的时间段,代表心室肌细胞开始去极化到结束复极化所需要的时间,与心率呈负相关。
二、滤波器的选择
1.肌电干扰的滤除—低通滤波器
通常来说,肌电信号的频率为20~5000HZ,其主要成分的频率与肌肉的类型有关,一般在30~300HZ,而心电信号的频率主要集中在5~20HZ,所以选择低通滤波器来滤除肌电干扰。
巴特沃斯滤波器的特点是通频带内的频率响应曲线最为平坦,没有起伏,而在阻频带则逐渐下降为零。巴特沃斯滤波器的振幅对角频率单调下降,并且滤波器的阶数越高,在阻频带幅度衰减速度越快,其他滤波器高阶的振幅对角频率图和低阶数的振幅对角频率有不同的形状。
2.工频干扰的抑制—带陷滤波器
工频干由于供电网络无所不在,因此50Hz的工频干扰是最普遍的,也是心电信号的主要干扰来源。50HZ陷波器的软件设计方法多种多样,常见方法有小波变换滤波、自适应滤波、模板匹配滤波等,但都需要手工计算获得滤波器的参数,运算比较复杂。
滤波器设计中,使用IIR滤波器,可使阶数降低,运算量减少,但破坏了相位特性;使用FIR滤波器既能得到很好的滤波效果,是波形失真达到最下,而且,FIR滤波器可以做成线性相位特性,这正好是心电信号滤波所需要的。
利用MATLAB设计FIR滤波器的方法有窗函数法、频率抽样法和切比雪夫逼近法等,本次课设采用窗函数法设计50HZ陷波滤波器。窗函数方法的基本思想是:首先根据要求选择一个适当的理想低通滤波器,因为其脉冲响应是非因果且无限长的,用最优化窗结构窗函数来截取它的脉冲响应,从而得到线性相位和因果的FIR滤波器。Kaiser窗是接近最优化窗结构的窗函数,它可以根据不同的参数调整滤波器的各项指标,因此采用Kaiser窗函数进行滤波器设计扰的抑制—带陷滤波器
3.基线漂移的纠正—零相移滤波器
零相移滤波器是指一个信号序列经过该滤波器滤波后相位不发生变化,即该滤波器系统函数的相位响应为零。显然,对于因果系统来说是不可能实现零相移的,在事先无法知道信号相位谱的情况下,实现零相移是不可能的。零相移只能是对非因果系统来说的。具体而言,零相移滤波器使用了当前信号点前面和后面的信号点所包含的信息,从本质上说就是使用了“未来的信息”来消除相位失真。
三、程序及结果
1.心电信号读取
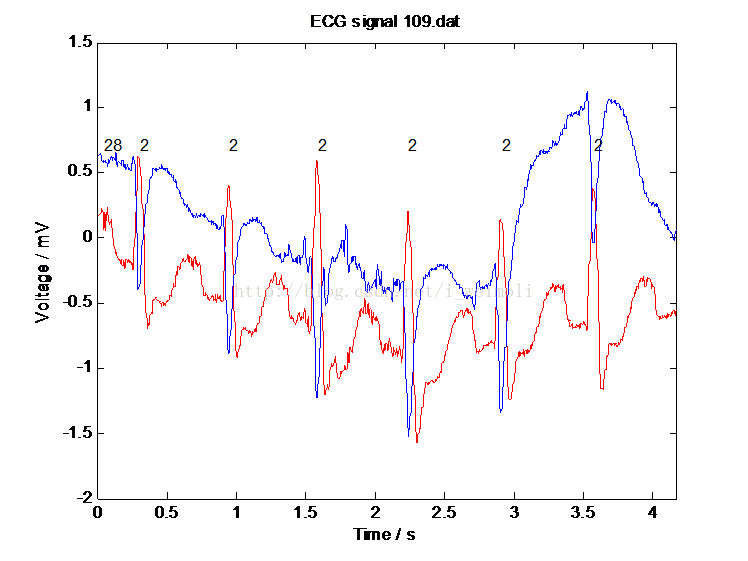
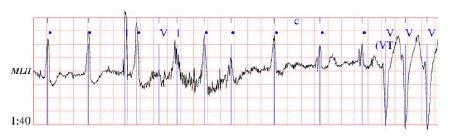
因为对MIT-BIH库不是很熟悉,在官网上看过之后,还是不懂(全英文,而且是医学方面的。。。)。所以,此处的心电信号的读取程序是来自网上的 rddata.m ,详细地可以参考点击打开链接。如果自己要用的话,在选取好要处理的心电信号后,把路径更改,并选取合适的样本数,就可以了。我选取的是MIT-BIH中的 109,样本数为1500,下图为心电信号读取后的图形:
图2 MIT-BIH库109心电信号图(双通道)
从图2红色曲线可以看到,波形上存在许多“毛刺”,并且其相位在发生变化(以波峰为例,各波峰大致不在一条水平线上,即所说的“基线漂移”),部分波形收到的干扰比较严重,比较符合对信号处理的要求。
2.心电信号的预处理
(1)肌电信号的滤除
- clc;
- %——————————低通滤波器滤除肌电信号——————————
- Fs=1500; %采样频率
- fp=80;fs=100; %通带截止频率,阻带截止频率
- rp=1.4;rs=1.6; %通带、阻带衰减
- wp=2*pi*fp;ws=2*pi*fs;
- [n,wn]=buttord(wp,ws,rp,rs,’s’); %’s’是确定巴特沃斯模拟滤波器阶次和3dB
- 截止模拟频率
- [z,P,k]=buttap(n); %设计归一化巴特沃斯模拟低通滤波器,z为极点,p为零点和k为增益
- [bp,ap]=zp2tf(z,P,k) %转换为Ha(p),bp为分子系数,ap为分母系数
- [bs,as]=lp2lp(bp,ap,wp) %Ha(p)转换为低通Ha(s)并去归一化,bs为分子系数,as为分母系数
- [hs,ws]=freqs(bs,as); %模拟滤波器的幅频响应
- [bz,az]=bilinear(bs,as,Fs); %对模拟滤波器双线性变换
- [h1,w1]=freqz(bz,az); %数字滤波器的幅频响应
- m=filter(bz,az,M(:,1));
- figure
- freqz(bz,az);title(‘巴特沃斯低通滤波器幅频曲线’);
- figure
- subplot(2,1,1);
- plot(TIME,M(:,1));
- xlabel(‘t(s)’);ylabel(‘mv’);title(‘原始心电信号波形’);grid;
- subplot(2,1,2);
- plot(TIME,m);
- xlabel(‘t(s)’);ylabel(‘mv’);title(‘低通滤波后的时域图形’);grid;
- N=512
- n=0:N-1;
- mf=fft(M(:,1),N); %进行频谱变换(傅里叶变换)
- mag=abs(mf);
- f=(0:length(mf)-1)*Fs/length(mf); %进行频率变换
- figure
- subplot(2,1,1)
- plot(f,mag);axis([0,1500,1,50]);grid; %画出频谱图
- xlabel(‘频率(HZ)’);ylabel(‘幅值’);title(‘心电信号频谱图’);
- mfa=fft(m,N); %进行频谱变换(傅里叶变换)
- maga=abs(mfa);
- fa=(0:length(mfa)-1)*Fs/length(mfa); %进行频率变换
- subplot(2,1,2)
- plot(fa,maga);axis([0,1500,1,50]);grid; %画出频谱图
- xlabel(‘频率(HZ)’);ylabel(‘幅值’);title(‘低通滤波后心电信号频谱图’);
- wn=M(:,1);
- P=10*log10(abs(fft(wn).^2)/N);
- f=(0:length(P)-1)/length(P);
- figure
- plot(f,P);grid
- xlabel(‘归一化频率’);ylabel(‘功率(dB)’);title(‘心电信号的功率谱’);
以上程序的结果如下:
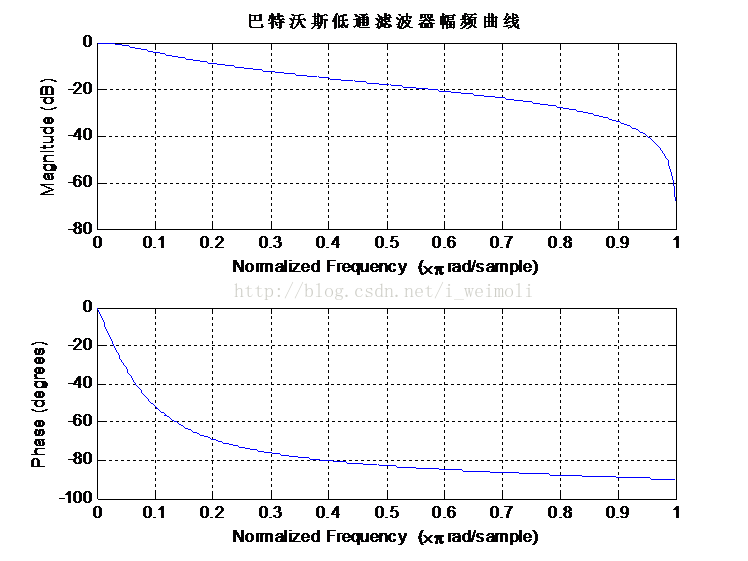
图3 图4
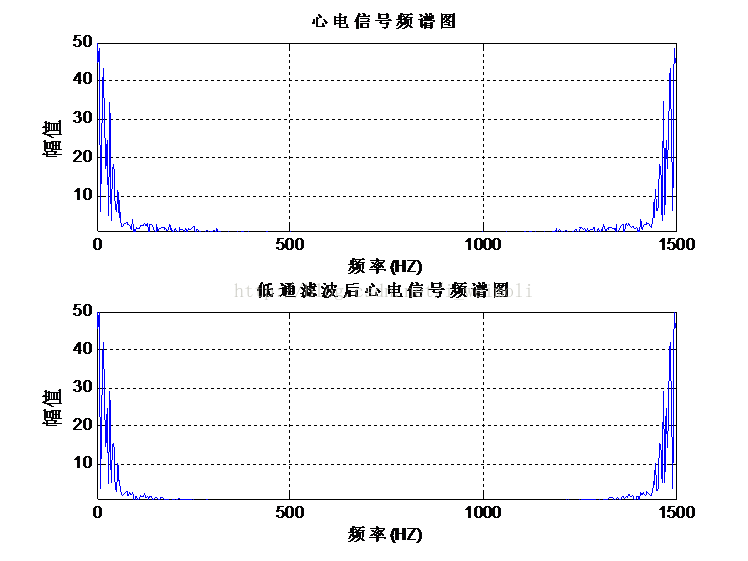
图5 图6
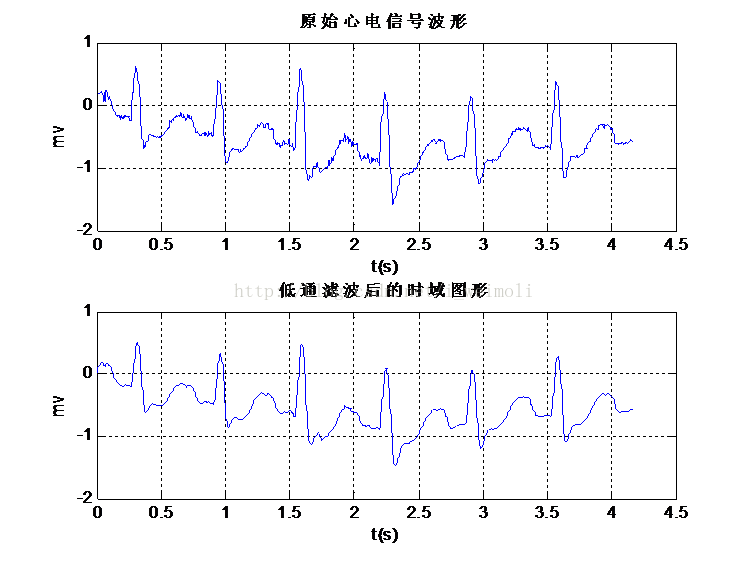
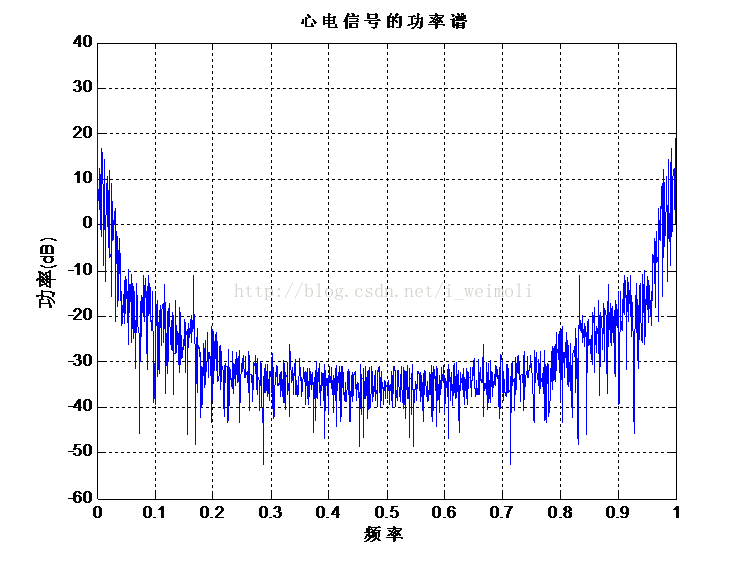
图3是所设计的巴特沃斯数字低通滤波器的幅频响应曲线,图3是在时域滤波前后心电信号的波形图,图5是在频域滤波前后心电信号的频谱图,图6是心电信号的功率谱图
(2)工频干扰的抑制
- %—————–带陷滤波器抑制工频干扰——————-
- %50Hz陷波器:由一个低通滤波器加上一个高通滤波器组成
- %而高通滤波器由一个全通滤波器减去一个低通滤波器构成
- Me=100; %滤波器阶数
- L=100; %窗口长度
- beta=100; %衰减系数
- Fs=1500;
- wc1=49/Fs*pi; %wc1为高通滤波器截止频率,对应51Hz
- wc2=51/Fs*pi ;%wc2为低通滤波器截止频率,对应49Hz
- h=ideal_lp(0.132*pi,Me)-ideal_lp(wc1,Me)+ideal_lp(wc2,Me); %h为陷波器
- 冲击响应
- w=kaiser(L,beta);
- y=h.*rot90(w); %y为50Hz陷波器冲击响应序列
- m2=filter(y,1,m);
- figure
- subplot(2,1,1);plot(abs(h));axis([0 100 0 0.2]);
- xlabel(‘频率(Hz)’);ylabel(‘幅度(mv)’);title(‘陷波器幅度谱’);grid;
- N=512;
- P=10*log10(abs(fft(y).^2)/N);
- f=(0:length(P)-1);
- subplot(2,1,2);plot(f,P);
- xlabel(‘频率(Hz)’);ylabel(‘功率(dB)’);title(‘陷波器功率谱’);grid;
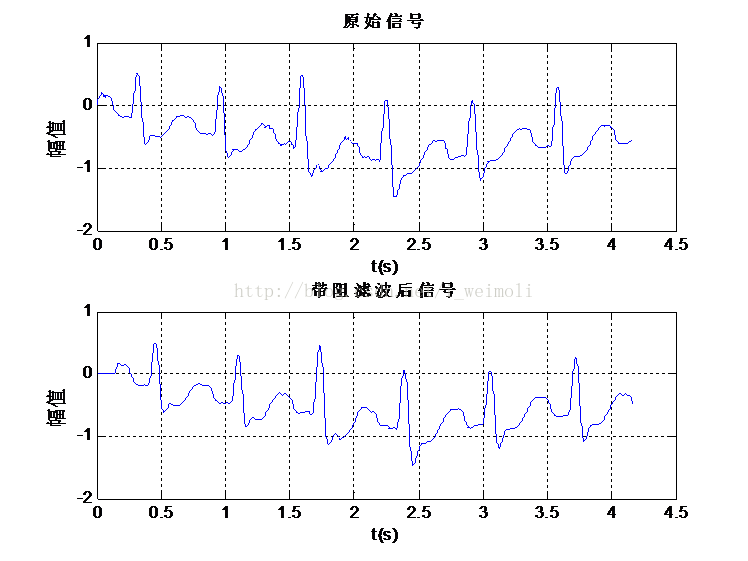
- figure
- subplot (2,1,1); plot(TIME,m);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘原始信号’);grid;
- subplot(2,1,2);plot(TIME,m2);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘带阻滤波后信号’);grid;
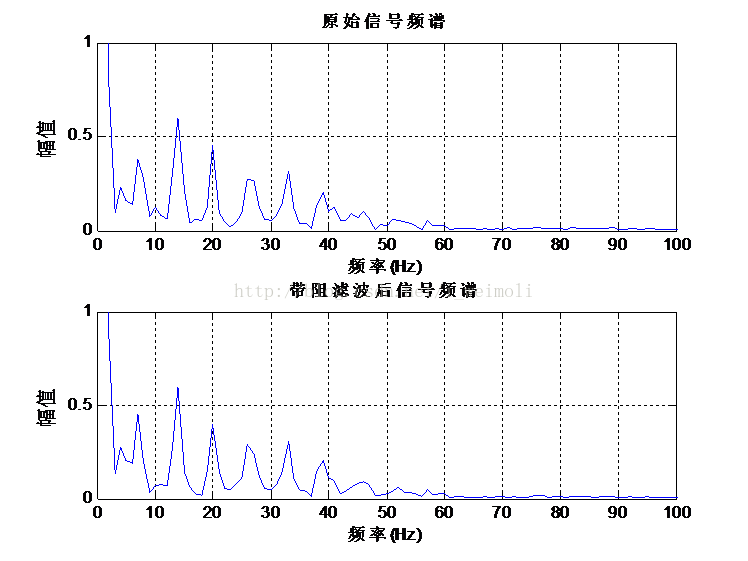
- figure
- N=512
- subplot(2,1,1);plot(abs(fft(m))*2/N);axis([0 100 0 1]);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘原始信号频谱’);grid;
- subplot(2,1,2);plot(abs(fft(m2))*2/N);axis([0 100 0 1]);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘带阻滤波后信号频谱’);grid;
- 其中,ideal_lp()函数在另一个M文件中,具体如下:
- %理想低通滤波器
- %截止角频率wc,阶数Me
- function hd=ideal_lp(wc,Me)
- alpha=(Me-1)/2;
- n=[0:Me-1];
- p=n-alpha+eps; %eps为很小的数,避免被0除
- hd=sin(wc*p)./(pi*p); %用Sin函数产生冲击响应
以上程序的结果如下:
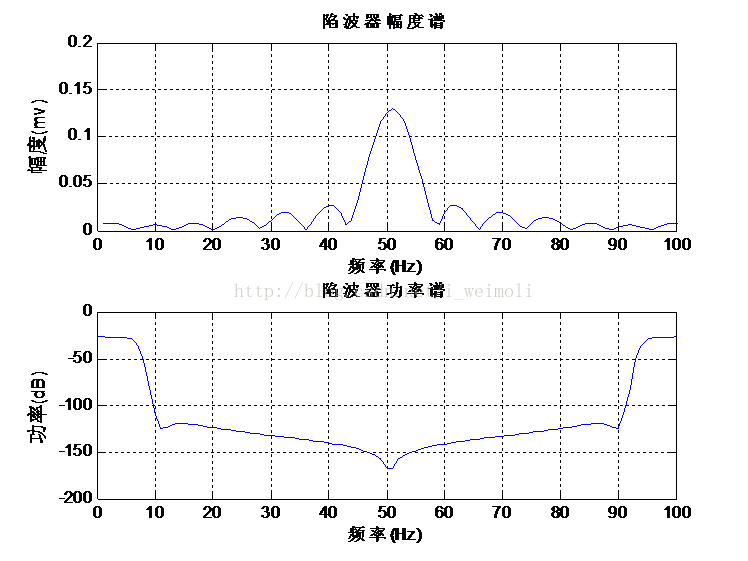
图7 图8
图9
图7是带陷滤波器的幅度谱和功率谱,从图中可以看到在50Hz处,滤波器的幅度很大,而且功率在-150以下,说明带陷性能较好。图8是在时域滤波前后的心电信号图,可以看出,滤波后波形有了略微的改善。图19是在频域滤波前后的心电信号频谱图。
(3)基线漂移的纠正
- %——————IIR零相移数字滤波器纠正基线漂移——————-
- Wp=1.4*2/Fs; %通带截止频率
- Ws=0.6*2/Fs; %阻带截止频率
- devel=0.005; %通带纹波
- Rp=20*log10((1+devel)/(1-devel)); %通带纹波系数
- Rs=20; %阻带衰减
- [N Wn]=ellipord(Wp,Ws,Rp,Rs,’s’); %求椭圆滤波器的阶次
- [b a]=ellip(N,Rp,Rs,Wn,’high’); %求椭圆滤波器的系数
- [hw,w]=freqz(b,a,512);
- result =filter(b,a,m2);
- figure
- freqz(b,a);
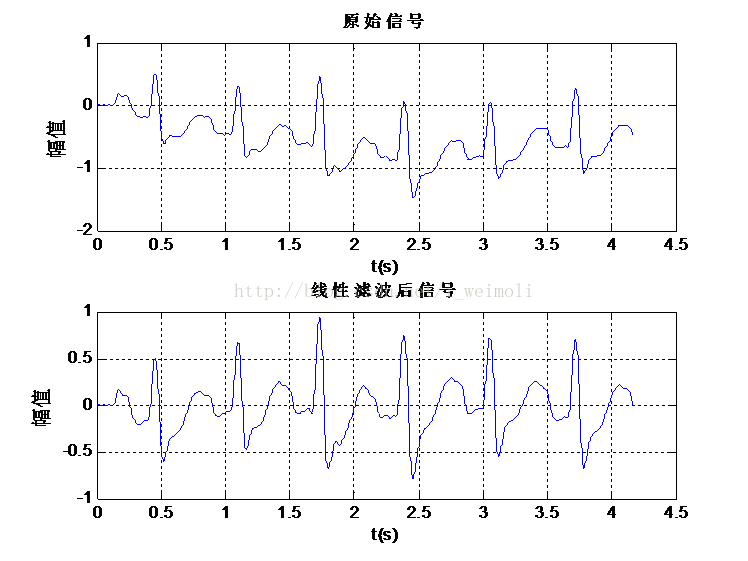
- figure
- subplot(211); plot(TIME,m2);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘原始信号’);grid
- subplot(212); plot(TIME,result);
- xlabel(‘t(s)’);ylabel(‘幅值’);title(‘线性滤波后信号’);grid
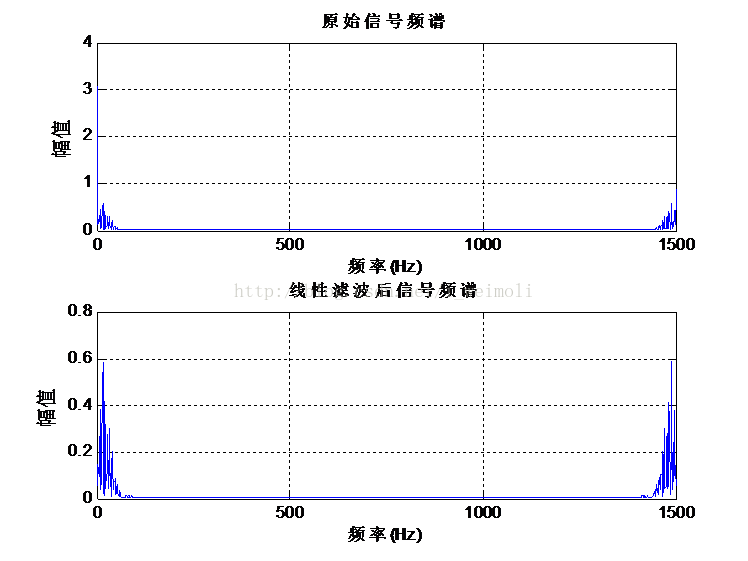
- figure
- N=512
- subplot(2,1,1);plot(abs(fft(m2))*2/N);
- xlabel(‘频率(Hz)’);ylabel(‘幅值’);title(‘原始信号频谱’);grid;
- subplot(2,1,2);plot(abs(fft(result))*2/N);
- xlabel(‘频率(Hz)’);ylabel(‘幅值’);title(‘线性滤波后’);grid;s
- ubplot(2,1,2);plot(abs(fft(result))*2/N);
- xlabel(‘线性滤波后信号频谱’);ylabel(‘幅值’);grid;
图10 图11
图10是在时域滤波前后的心电信号图,可以看出,滤波后基线漂移得到了改善,图11是在频域滤波前后的心电信号频谱图。