前言

在经典组合优化问题中的优秀算法自从上个世纪九十年代以来，分为两个突出的弹射算法，一个是LK启发式，一个是eject chain算法。前者在dismacs算法竞赛上大放异彩，经过算法的改良多种LK的分支都有不错的效果，且现在也有工业化的版本求解器，做的相当成熟。后者的弹射链算法作为主流之一，但是慢慢发展未能做起来，似乎有点停滞不前。本文对起进行较为基础的原始和理论的介绍，经过介绍可以分析得出，理论上弹射链算法是完备的，有很多改良和应用的空间，虽然现在较为没落，但是不失为一种探索的空间，也是值得学习和介绍的。

Eject Chain 算法

弹射链中 cycle and stem 的结构介绍

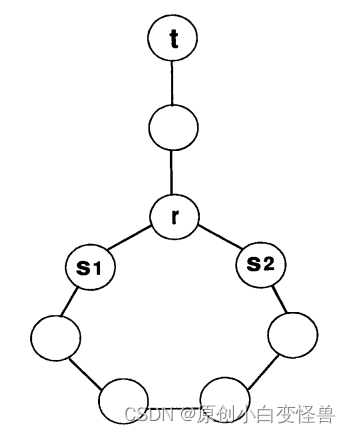
在这里插入图片描述
上图就是基本的弹射链的回路和茎的structure，r代表root根，t代表stem茎，s1和s2是子根subroot，其他没有标注的结点就是一些普通的结点。

Subpath Election Method

在这里插入图片描述
步骤①：初始设置r=t，原始集合PC和SC，PC={r}，SC为空

步骤②：在tour的一个子路径 j,…,k中，且子路径的结点都不在PC和SC中。将j’j,和kk’‘删除，j’和k’‘分别是j和k的左右两个结点，并且将旅行subpath j,k中的j和k的位置用j’和k’'来代替，弥补空洞。
在这里插入图片描述

步骤③：在②的基础上，更细t=k，茎j和k加入PC中，j‘和k’‘加入SC中，如果加入PC的结点是一个子根subroot，则它之后不能再被操作。
在这里插入图片描述

步骤④：重复以上①②③直到达到终止条件。

一些基础的 STEM-AND-CYCLE RULES

上面一part讲的是如何从子路径中删除和弹出边，现在介绍的是弹出的变之后是怎么加入茎和回路的结构当中，以生成新的可行解的过程的一些规则。
在这里插入图片描述
上面这张图说的是四条规则来生成可变路径，规则1和2是主要的，3和4是一些完善和补充。
下面让我们来看看四种规则的具体操作实例

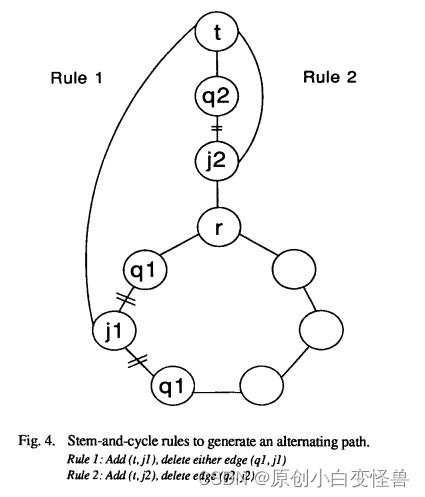
图中，下面一圈是cycle，上面是茎。规则①中，在将t和j1相连的时候，为了仍保持cycle-and-stem的结果，需要将q1和j1之间的变删除，然后q1作为新的t。
规则②中，如果t和茎中的j2相连，则需要删除t和j2之间的结点的边，图中是j2和q2之间的边，然后将q2作为新的t
下面的规则三和四是对一和二的补充，让我们也来看看
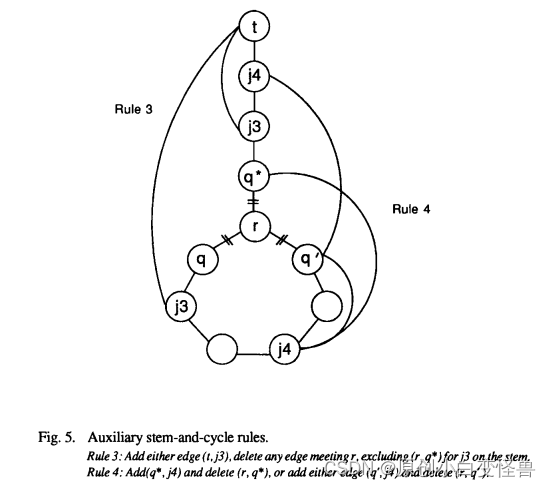
在这里插入图片描述
规则③中，如果我们将t和cycle中的j3相连，把j3和q的边删去，q成为新的t。
如果t是和茎中的j3相连，则把q和r之间的边删去，让原来的茎形成cycle，原来stem破坏成stem，q成为新的t

在规则④中有两种情况，如果q’和茎中的j4相连，我们把r和q‘之间的边断开，其余不变
如果q和cycle 中的j4相连，我们把q和r断开

结论、分析和结束语

为什么弹射链理论分析上效果会不错，因为寻优中，LK算法所能达到的case，它都能达到，LK不能演算出来的情况也能过做到，理论上探寻的空间是更大的，寻找到局部最优的可能性行是以LK算法的情况为下界的。
分享这篇文章的原因也是历史遗留问题，下载下来一直没有看，最近跑实验的过程中想着还是不能太摆烂，把这篇也补上，万一以后没有啥时间看了，不留遗憾。
其实思考来，这篇文章的思路和想法都是不错的，有很多是错的空间和探索的可能性存在，这里就不再详细展开了。
如果读者感兴趣的话，可以参看下面的参考文献。

参考文献

Glover F. New ejection chain and alternating path methods for traveling salesman problems[M]//Computer science and operations research. Pergamon, 1992: 491-509.