文章目录
- 数字三角形模型
- 摘花生(线性DP)
- 最低通行费(线性DP+曼哈顿距离 / 记忆化搜索)⚡🎈
- 方格取数(线性DP)
- 传纸条
- 最长上升子序列模型
- 怪盗基德的滑翔翼(线性DP、LIS)
- 登山(线性DP、LIS模板题)
- 合唱队形(LIS 线性DP)
- 友好城市(LIS优化版+模型转换)🔥👍
- 最大上升子序列和
- 拦截导弹(LIS/最长不上升子序列)
- 导弹防御系统(DFS+线性DP😢🔺❗)
- 最长公共上升子序列(🔺)
- 状态机模型
数字三角形模型
摘花生(线性DP)

public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 110;static int[][] dp = new int[N][N];static int[][] a = new int[N][N];static int t = 0;static int r = 0, c = 0;public static void main(String[] args) throws Exception{t = Integer.parseInt(br.readLine());while(t-- > 0) {String[] rc = br.readLine().split(" ");r = Integer.parseInt(rc[0]);c = Integer.parseInt(rc[1]);for(int i = 1; i <= r; i++) {String[] aa = br.readLine().split(" ");for(int j = 1; j <= c; j++) {a[i][j] = Integer.parseInt(aa[j - 1]);}}for(int i = 1; i <= r; i++) {for(int j = 1; j <= c; j++) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + a[i][j];}}System.out.println(dp[r][c]);}}
}
最低通行费(线性DP+曼哈顿距离 / 记忆化搜索)⚡🎈

法一:线性DP
这题目最重要的是根据必须在(2N-1)个单位时间内穿越出去,推导出此题的解题的重要性质。
曼哈顿距离:
两个点在标准坐标系上的绝对轴距总和,d=|x2−x1|+|y2−y1
此题虽然说可以向上下左右四个方向移动,但是根据2n-1个单位时间的限制结合曼哈顿距离,我们可以得到:
(1,1)->(n,n)的曼哈顿距离为2n-2,但是题目要求在2n-1的单位时间穿越出去,所以我们每次走一步必须可以使曼哈顿距离缩短1,否则是无用的,因此我们得到我们只能向下或向右走,这样才能每走一步就距离终点更近。这样的话就和最经典的上一题👆基本差不多啦~

public class Main{static Scanner sc = new Scanner(System.in);static int N = 110;static int[][] dp = new int[N][N];static int Inf = 0x3f3f3f3f;static int n = 0;static int[][] w = new int[N][N];public static void main(String[] args) {n = sc.nextInt();for(int i = 1; i <= n; i++) {for(int j = 1; j <= n; j++) {w[i][j] = sc.nextInt();}}//注意必须从0开始赋值for(int i = 0; i <= n; i++) {for(int j = 0; j <= n; j++) {dp[i][j] = Inf;}}dp[1][1] = w[1][1];for(int i = 1; i <= n; i++) {for(int j = 1; j <= n; j++) {dp[i][j] = Math.min(dp[i][j],dp[i][j - 1] + w[i][j]);dp[i][j] = Math.min(dp[i][j],dp[i - 1][j] + w[i][j]);}}System.out.println(dp[n][n]);}
}
法二:记忆化搜索
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Scanner;public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 110;static int[][] f = new int[N][N];static int Inf = 0x3f3f3f3f;static int n = 0;static int[][] w = new int[N][N];public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());for(int i = 1; i <= n; i++) {String[] ww = br.readLine().split(" ");for(int j = 1; j <= n; j++) {w[i][j] = Integer.parseInt(ww[j - 1]);}}// for(int i = 0; i < N; i++) {
// for(int j = 0; j < N; j++) {
// f[i][j] = -1;
// }
// }int ans = dfs(n,n);System.out.println(ans);}private static int dfs(int x, int y) {if(f[x][y] != 0) {return f[x][y];}if(x == 1 && y == 1) {f[x][y] = w[x][y];return f[x][y];}if(x < 1 || y < 1) {return Inf;}int t = Inf;t = Math.min(t,dfs(x - 1,y) + w[x][y]);t = Math.min(t,dfs(x, y - 1) + w[x][y]);return f[x][y] = t;}
}
方格取数(线性DP)

此题和上面的dp差不多,也是从左上角到右下角,但是需要注意点饿是我们需要找到两条路径的最大和,第一感觉是进行两次上面的操作,但是是不可以的,因为没走过一点会置为0,当我们选定了第一条路径后,第一条路径走过的地方会置为0,我们在第二次进行时,并不能保证此种选择是两条路径之和最大的。
设dp[i][j][p][q]为两条路径分别从起点到i,j和p,q的路径的最大和。
需要注意的是如果我们到达同一点的时候,会导致同一点的数被取了两遍,此时我们需要减去一次,注意我们是在所有情况中取的最大值,只有在走到同一点的时候才会重复取两次。
public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 12;static int[][][][] dp = new int[N][N][N][N];static int[][] a = new int[N][N];static int n = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());while(true) {String[] xyz = br.readLine().split(" ");int x = Integer.parseInt(xyz[0]);int y = Integer.parseInt(xyz[1]);int z = Integer.parseInt(xyz[2]);if(x == 0 && y == 0 && z == 0) {break;}a[x][y] = z;}for (int i = 1; i <= n; i ++) {for (int j = 1; j <= n; j ++) {for (int p = 1; p <= n; p ++) {for (int q = 1; q <= n; q ++) {dp[i][j][p][q] = Math.max(dp[i][j][p][q], dp[i-1][j][p-1][q]+a[i][j]+a[p][q]);dp[i][j][p][q] = Math.max(dp[i][j][p][q], dp[i-1][j][p][q-1]+a[i][j]+a[p][q]);dp[i][j][p][q] = Math.max(dp[i][j][p][q], dp[i][j-1][p-1][q]+a[i][j]+a[p][q]);dp[i][j][p][q] = Math.max(dp[i][j][p][q], dp[i][j-1][p][q-1]+a[i][j]+a[p][q]);if (i == p && j == q) {dp[i][j][p][q] -= a[i][j];
// System.out.println(111);}}}}}System.out.println(dp[n][n][n][n]);}
}
传纸条

此题目和上面的方格取数基本是一样的。
此题目描述是:从左上角传到右下角和从右下角传到左上角各一次,但是此是一个点不能重复走两次(和上面的方格取数的走完会清零不同),首先,我们可以转换为都是从左上角开始向右下角同时开始,此时和方格取数差不多了)
🌈重点需要理解的是:
方格取数是可以两次重复走到一个地方,但是最优解肯定不会走相同的地方。
本题是不可以走相同的地方。
经过转换后,所以两道题的代码基本是一样的。
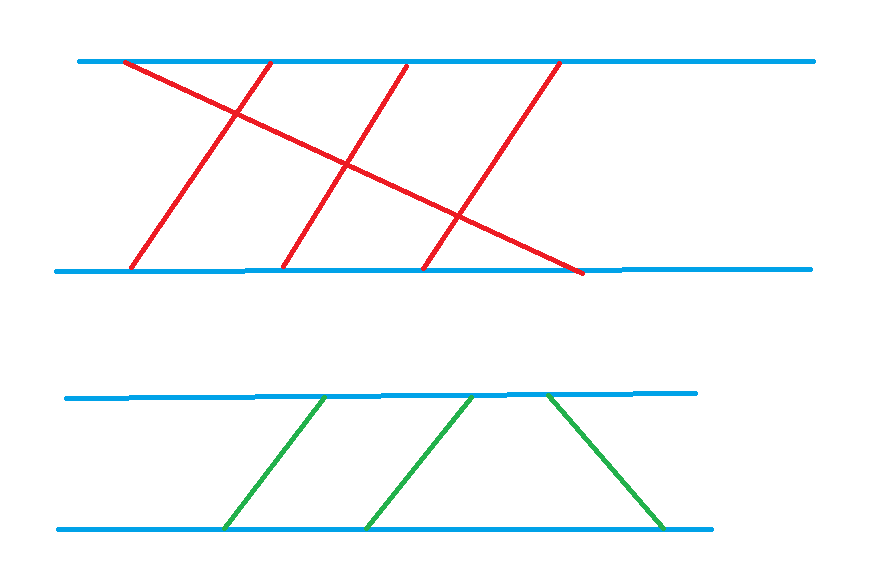
下面的证明是从大佬的题解看到的大佬题解对于没有交点的情况,我们不需要考虑。 主要是证明为什么不会取到走到同一点的情况。
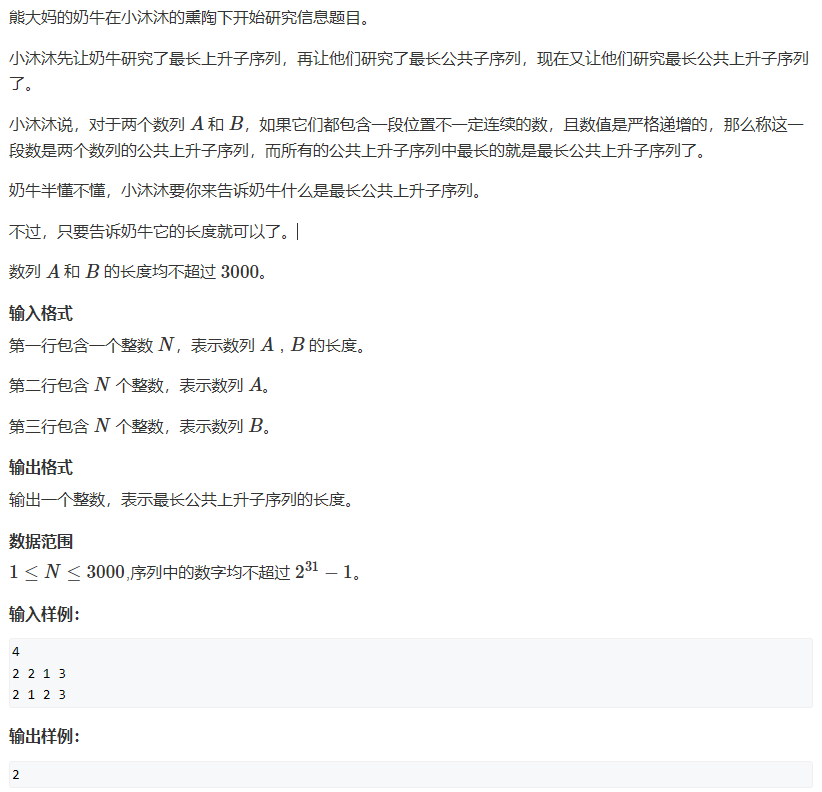
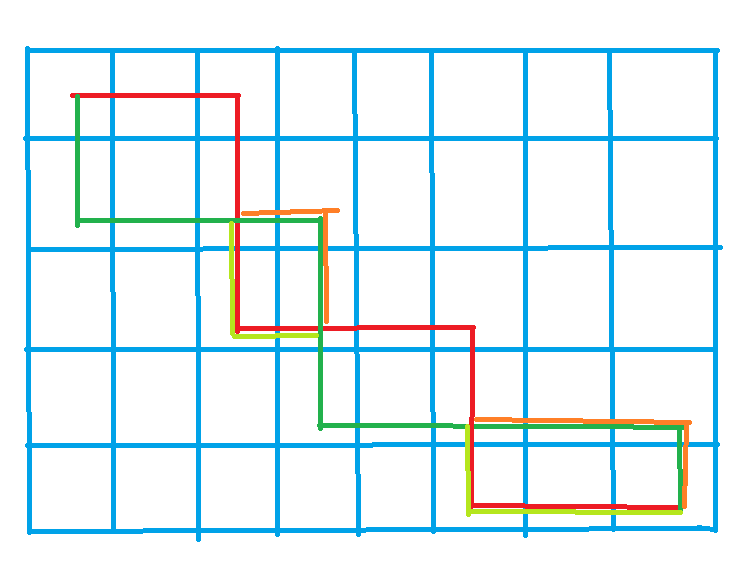
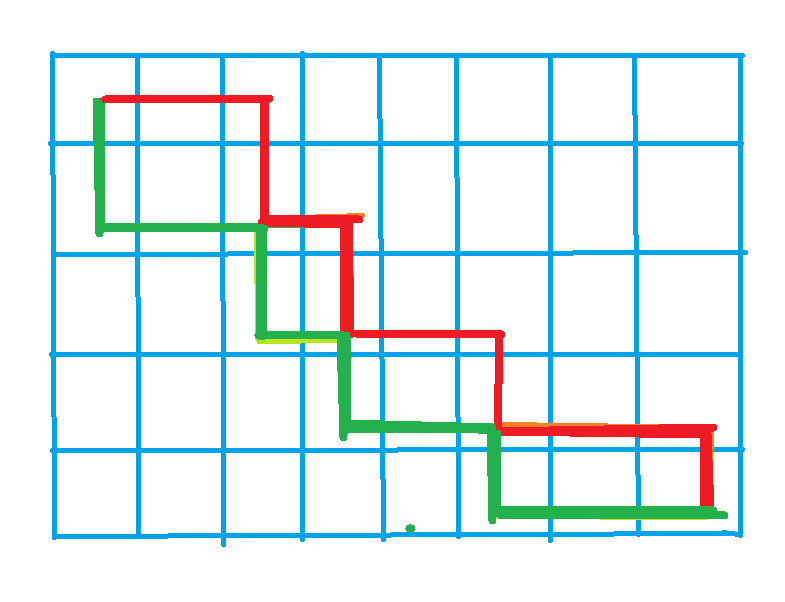
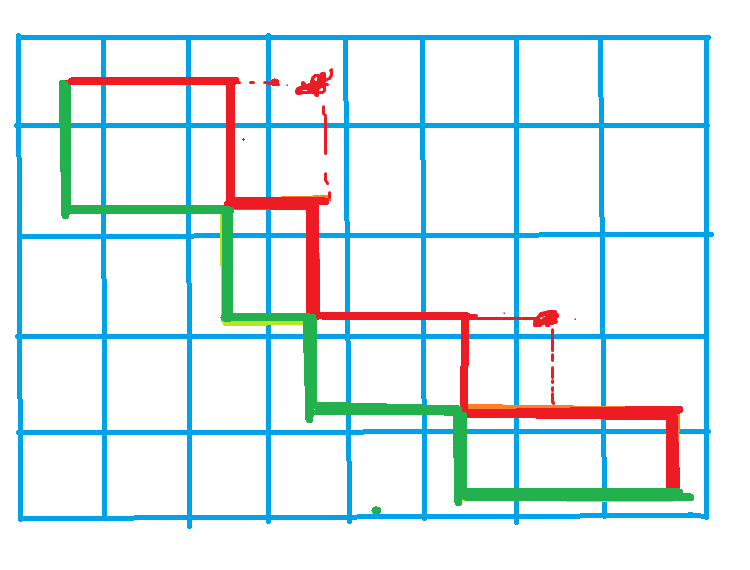
比如上方红色是A路线,绿色是B路线。 存在相交的地方,我们只需要交换路线即可,对答案并没有任何影响。
用橙色代表与绿色交换后的红色,用亮绿色代表与红色交换后的绿色,可以得到如下路线:
但是很明显可以看到还是有同时走到的点,但是由于
这个条件,我们可以知道绕路走的
话肯定是比走同一个点更优。我们可以寻找绿色绕路或者蓝色绕路的最优值。
最长上升子序列模型
怪盗基德的滑翔翼(线性DP、LIS)


很明显就是最长上升子序列,它可以选择从最高楼层的顶部开始进行下落。但是题目中说了它可以从任何一个楼开始,但是开始后就不能改变方向,所以有两种情况:
(1)从左到右,最高的在右边,然后我们需要求的就是最长上升子序列(对应于样例中的2、3)需要求最长上升子序列
(2)从右往左飞,最高的在左边,我们需要求得就是最长下降子序列,但是本质都是一样的,进行两次即可。
public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 110;static int[] h = new int[N];static int[] dp = new int[N]; //最长上升子序列static int[] dp2 = new int[N]; //最长下降子序列static int k = 0, n = 0;public static void main(String[] args) throws Exception{k = Integer.parseInt(br.readLine());while(k-- > 0) {n = Integer.parseInt(br.readLine());String[] hh = br.readLine().split(" ");for(int i = 1; i <= n; i++) {h[i] = Integer.parseInt(hh[i - 1]);}for(int i = 1; i <= n; i++) {dp[i] = 1;for(int j = 1; j < i; j++) {if(h[j] < h[i]) {dp[i] = Math.max(dp[i],dp[j] + 1); }}}int ans = 0;for(int i = 1; i <= n; i++) {ans = Math.max(dp[i],ans);}for(int i = 1; i <= n; i++) {dp2[i] = 1;for(int j = 1; j < i; j++) {if(h[j] > h[i]) {dp2[i] = Math.max(dp2[i],dp2[j] + 1); }}}for(int i = 1; i <= n; i++) {ans = Math.max(dp2[i],ans);}System.out.println(ans);}}
}
对于第一种情况:就是求最长上升子序列;
第二种情况:就是求最长下降子序列;
第三种情况:就是求最长上升子序列和最长下降子序列的最大值。
综上,我们只需要求解最长上升子序列和最长下降子序列的最大值。
登山(线性DP、LIS模板题)
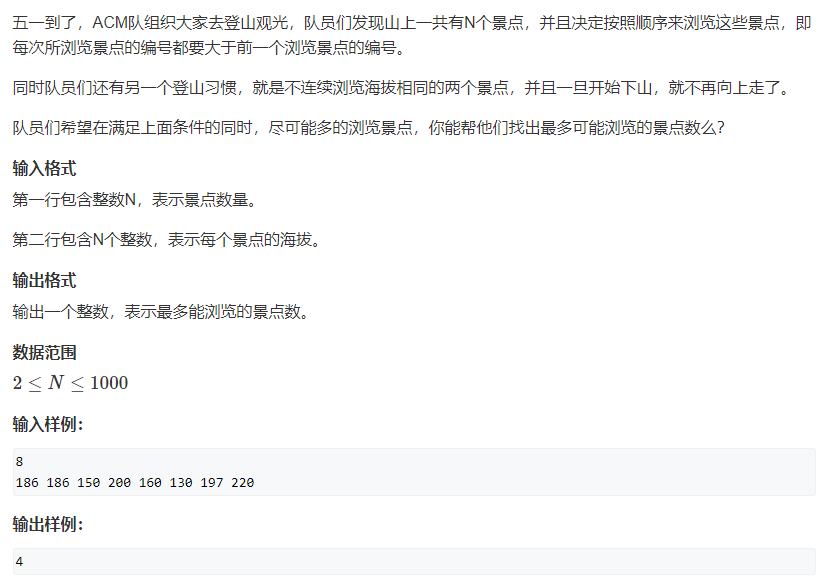
第一次看题觉得和上面的差不多,但是需要注意,此题是可以下山,就是下山的过程中也是可以看的,我们需要求得是两者的和,
但是我们需要注意的是,up和down是有区别的,和上一题不同,因为我们求最长上升子序列的时候,求得是以i为结尾的最长上升子序列,那么如果我们对于down和up都这样求得话肯定是不行的,我们需要稍微改变一下down[]的定义:
up[i]:以i为结尾的最长上升子序列
down[i]:以i为开头的最长下降子序列。

public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 1100;static int[] h = new int[N];static int[] up = new int[N]; //最长上升子序列static int[] down = new int[N];static int k = 0, n = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());String[] hh = br.readLine().split(" ");for(int i = 1; i <= n; i++) {h[i] = Integer.parseInt(hh[i - 1]);}for(int i = 1; i <= n; i++) {up[i] = 1;for(int j = 1; j < i; j++) {if(h[j] < h[i]) {up[i] = Math.max(up[i],up[j] + 1); }}}//down[i]代表以i为左端点的最长下降子序列 for(int i = n; i >= 1; i--) {down[i] = 1;for(int j = n; j > i; j--) {if(h[i] > h[j]) {down[i] = Math.max(down[i],down[j] + 1);}}}int ans = 0;for(int i = 1; i <= n; i++) {ans = Math.max(ans,up[i] + down[i] - 1);
// System.out.println(i + " " + up[i] + " " + down[i] + " " + ans);}System.out.println(ans);}
}
合唱队形(LIS 线性DP)
和上面上面的登山可以说是完全一样,只是此题需要输出n-ans
很明显我们通过上面的代码可以求出最长上升和最长下降的和的最大,即为最后合照剩下的人,那么需要出列的人数肯定就是原来的总人数-最后剩下的人。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = 1100;static int[] h = new int[N];static int[] up = new int[N]; //最长上升子序列static int[] down = new int[N];static int k = 0, n = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());String[] hh = br.readLine().split(" ");for(int i = 1; i <= n; i++) {h[i] = Integer.parseInt(hh[i - 1]);}for(int i = 1; i <= n; i++) {up[i] = 1;for(int j = 1; j < i; j++) {if(h[j] < h[i]) {up[i] = Math.max(up[i],up[j] + 1); }}}//down[i]代表以i为左端点的最长下降子序列 for(int i = n; i >= 1; i--) {down[i] = 1;for(int j = n; j > i; j--) {if(h[i] > h[j]) {down[i] = Math.max(down[i],down[j] + 1);}}}int ans = 0;for(int i = 1; i <= n; i++) {ans = Math.max(ans,up[i] + down[i] - 1);
// System.out.println(i + " " + up[i] + " " + down[i] + " " + ans);}System.out.println(n - ans);}
}
友好城市(LIS优化版+模型转换)🔥👍
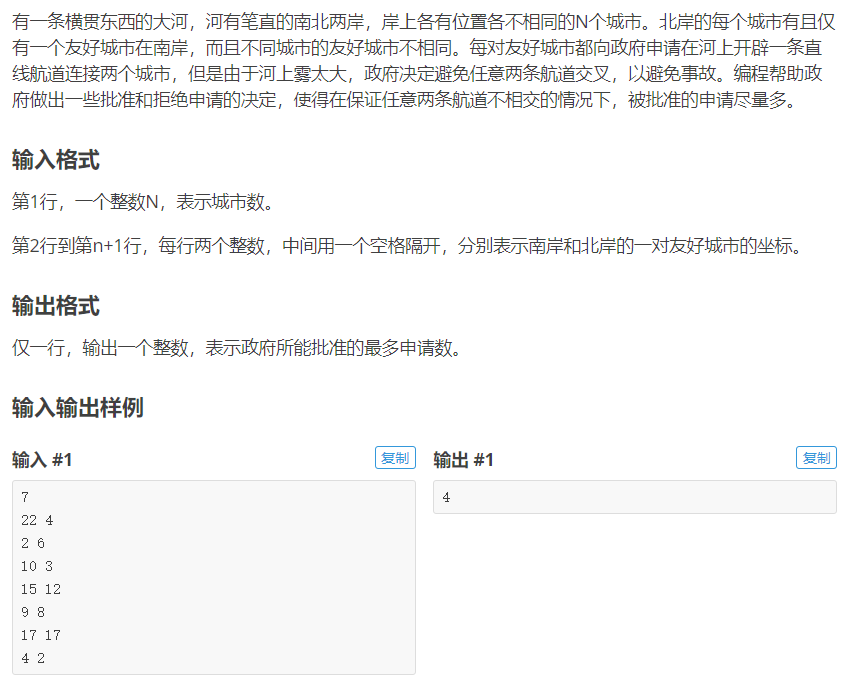
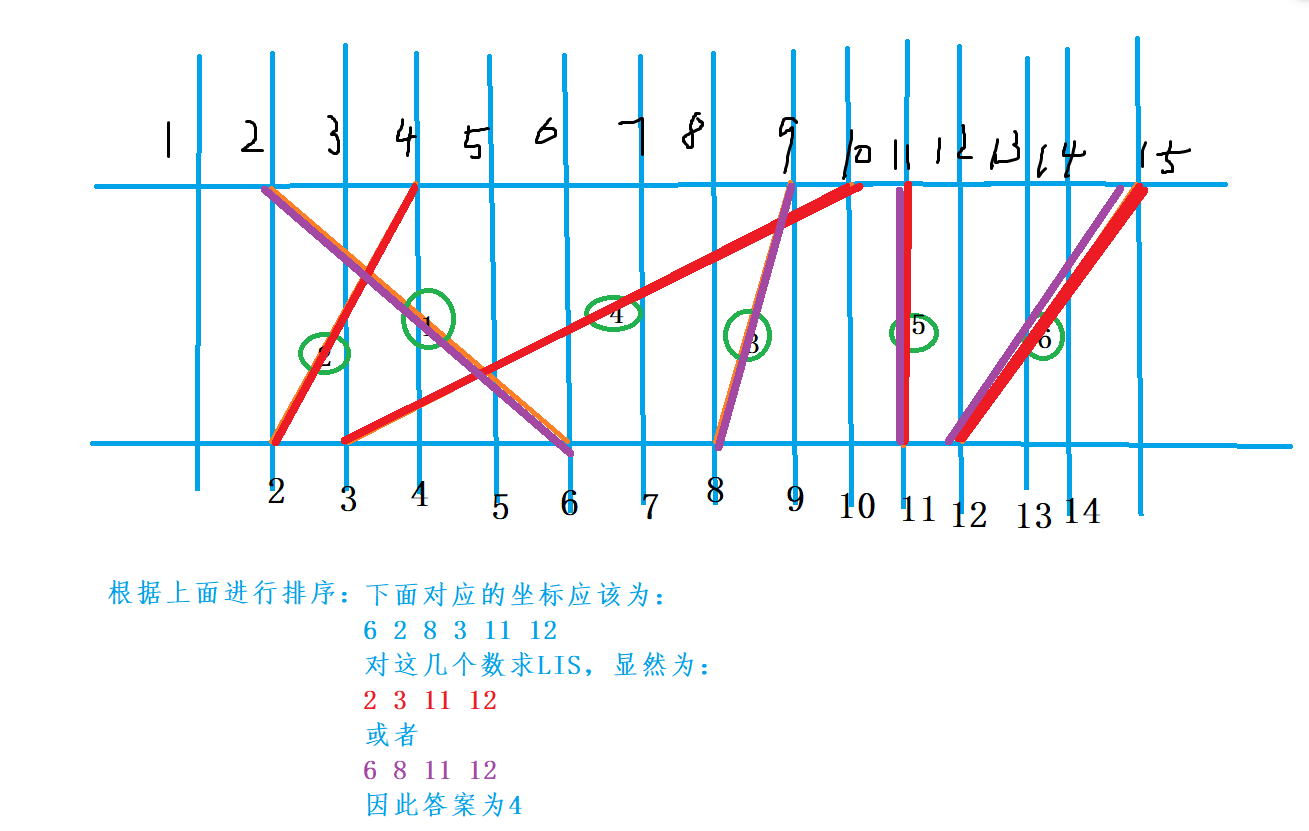
这题需要通过画图去转换,否则很难直接看出来:
很明显红色的是不可以的,绿色这种建桥方式是可行的。 我们可以看到只要两岸的城市都保证是上升子序列即可。 但是他们之间存在各自的一对一关系,起初想着分别求LIS,然后求两者最小值的最大值,这种方法是不可行的,主要是我们需要保证他们之间的对应关系。
那么我们可以通过一边对这对对应关系进行排序,然后再对另一边求最长上升子序列即为答案。
画图理解比较直观一点:
上面的两种情况都是可以的,所以最终答案就为4
题目理解完毕,开始写代码(主要就是LIS)
public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = (int) (2e5 + 10);static node[] info = new node[N];static int[] dp = new int[N]; //最长上升子序列static int k = 0, n = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());for(int i = 1; i <= n; i++) {String[] xy = br.readLine().split(" ");info[i] = new node();info[i].x = Integer.parseInt(xy[0]);info[i].y = Integer.parseInt(xy[1]);}Arrays.sort(info,1, 1 + n, new cmp());for(int i = 1; i <= n; i++) {dp[i] = 1;for(int j = 1; j < i; j++) {if(info[j].y < info[i].y) {dp[i] = Math.max(dp[i],dp[j] + 1);}}}int ans =0;for(int i = 1; i <= n; i++) {ans = Math.max(ans,dp[i]);}System.out.println(ans);}
}
class node{int x,y;
}
class cmp implements Comparator<node>{@Overridepublic int compare(node o1, node o2) {return o1.x - o2.x;}}
显然上面的代码时间复杂度为O(n2)
显然是过不了的,那么我们就需要使用二分优化的LIS(Nlogn)
主要思想就是,在满足最长上升子序列的前提下,尽可能增大结尾的潜能
使用q[]数组存储所有不同长度的上升子序列的结尾的最小值。
每加进来一个数,通过在q中查找最大的小于ai的数,并将ai接上去,q[r+1]=a[i]
下面可以略:主要解释LIS的原理:
✍
主要是因为,能接在更小的数后面的数肯定更多
比较绕的一点是,如果此时加入的数比结尾小,我们需要在q中查找大于等于它的数去替换,那么可能出现我们这个数比后买你的下标大 比如1 2 78
此时来了个5,我们需要用5替换7.但是显然5的下标肯定比7的大,但是这对于仅仅求最长上升子序列的长度是没有影响的,因为5后面的数的下标肯定是都大于5的,假如5后面没有数了,那么此时1
2 58
在序列里,所有最终答案为4,其实可以看作和5个7没有环保是等价的,我们将7换为5只是为了给后面造成更大的机会,比如5后买还有6,7,那么此时1
2 5 8,6进来找到8,进行替换为1 2 5 6然后7直接放后面 12 5 6
7这样就会比之前5和7不换序列更长。需要仔细体会!!!确实比较绕。
public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = (int) (2e5 + 10);static node[] info = new node[N];static int k = 0, n = 0;static int[] q = new int[N];static int cnt = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());for(int i = 1; i <= n; i++) {String[] xy = br.readLine().split(" ");info[i] = new node();info[i].x = Integer.parseInt(xy[0]);info[i].y = Integer.parseInt(xy[1]);}Arrays.sort(info,1, 1 + n, new cmp());// for(int i = 1; i <= n; i++) {
// dp[i] = 1;
// for(int j = 1; j < i; j++) {
// if(info[j].y < info[i].y) {
// dp[i] = Math.max(dp[i],dp[j] + 1);
// }
// }
// }q[++cnt] = info[1].y;for(int i = 2; i <= n; i++) {if(info[i].y > q[cnt]) {q[++cnt] = info[i].y;}else {int tmp = find(info[i].y);q[tmp] = info[i].y;}}System.out.println(cnt);}//找最大的小于x的数:找>=x的第一个数private static int find(int x) {int l = 1, r = cnt;int res = -1;while(l <= r) {int mid = (l + r) >> 1;if(q[mid] >= x) {res = mid;r = mid - 1;}else {l = mid + 1;}}return res;}
}
class node{int x,y;
}
class cmp implements Comparator<node>{@Overridepublic int compare(node o1, node o2) {return o1.x - o2.x;}}
完美AC!
最大上升子序列和
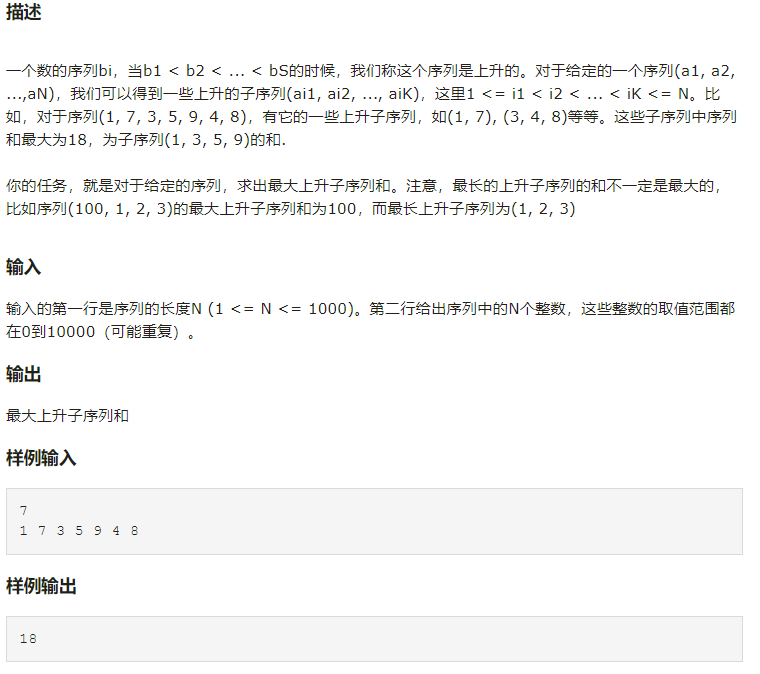
本质还是最长上升子序列,此时代表的是: dp[i]代表以a[i]结尾最大上升子序列和,
当a[j] < a[i]时候,我们改变之前的+1,为加当前这个数,注意是a[i]不是a[j]
public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = (int) (2e5 + 10);static int[] dp = new int[N]; //最长上升子序列static int k = 0, n = 0;static int[] q = new int[N];static int cnt = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());String[] aa = br.readLine().split(" ");for(int i = 1; i <= n; i++) {q[i] = Integer.parseInt(aa[i - 1]);}for(int i = 1; i <= n; i++) {dp[i] = q[i];for(int j = 1; j < i; j++){if(q[j] < q[i]) {dp[i] = Math.max(dp[i], dp[j] + q[i]);}}}int ans = 0;for(int i = 1; i <= n; i++) {ans = Math.max(ans,dp[i]);}System.out.println(ans);}
}
拦截导弹(LIS/最长不上升子序列)
✍
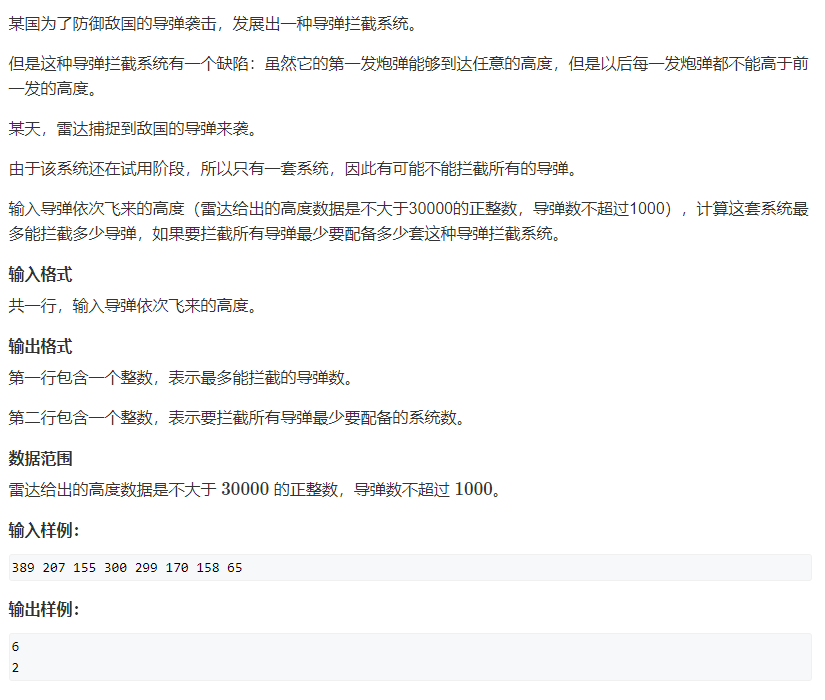
题目描述很明确,就是求最长不下降子序列,只需要改变求最长上升子序列时的转移条件即可。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;public class Main{static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int N = (int) (2e5 + 10);static int[] dp = new int[N]; //最长不上升子序列static int k = 0, n = 0;static int[] q = new int[N];static int cnt = 0;public static void main(String[] args) throws Exception{n = Integer.parseInt(br.readLine());String[] aa = br.readLine().split(" ");for(int i = 1; i <= n; i++) {q[i] = Integer.parseInt(aa[i - 1]);}for(int i = 1; i <= n; i++) {dp[i] = 1;for(int j = 1; j < i; j++){if(q[j] >= q[i]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}int ans = 0;for(int i = 1; i <= n; i++) {ans = Math.max(ans,dp[i]);}System.out.println(ans);}
}
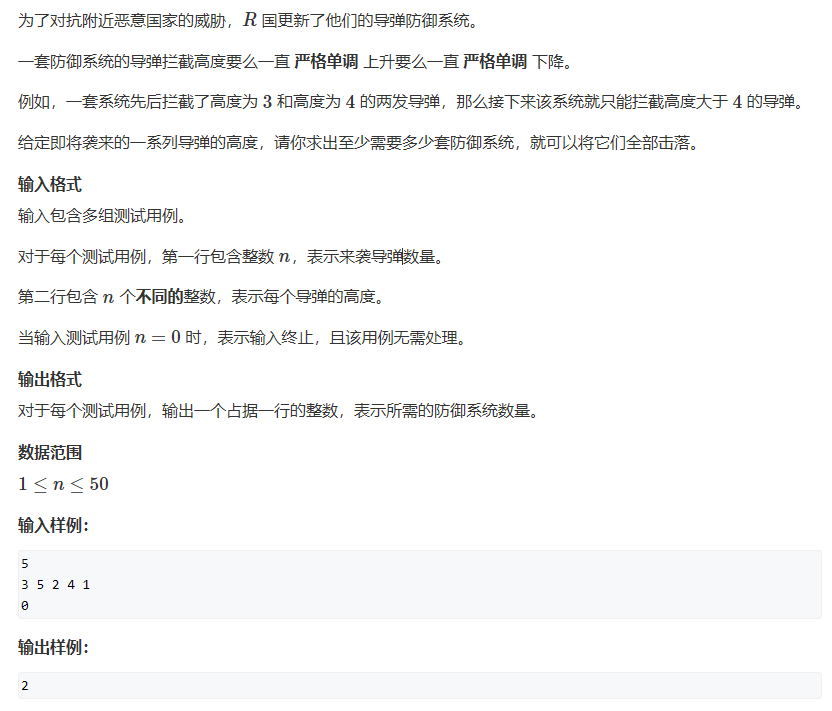
导弹防御系统(DFS+线性DP😢🔺❗)
✍
最长公共上升子序列(🔺)
✍