机器学习（十二）-基于规则的分类器

原创不易，转载前请注明博主的链接地址：Blessy_Zhu https://blog.csdn.net/weixin_42555080
本次代码的环境：
运行平台： Windows
Python版本： Python3.x
IDE： PyCharm
　

一算法简介

基于规则的分类器是使用一组"if…then…"规则来对记录进行分类的技术。
Rule: (条件)-----> y

where
- 条件是属性的合取
- y 是类标号
规则的左边称为规则前件或前提（ rule antecedent or precondition）
规则右边称为规则后件（ rule consequent）
例如：
(Blood Type=Warm) ^(Lay Eggs=Yes) —> Birds
(Taxable Income < 50K)^ (Refund=Yes) —> Evade=No

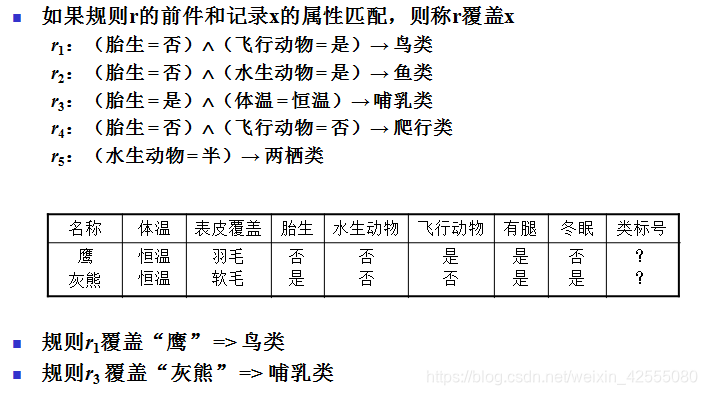
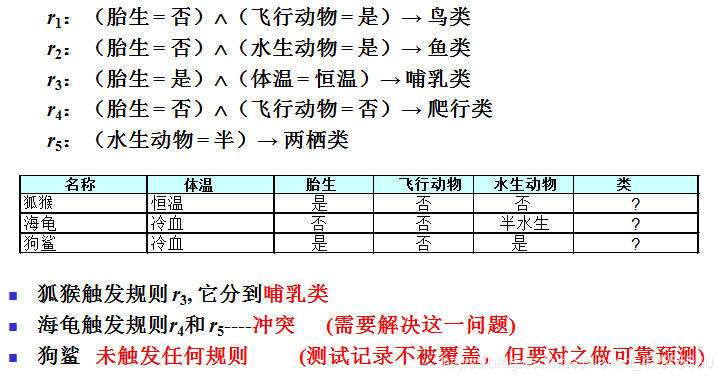
二规则的质量评价标准

一般用覆盖率（coverage）和准确率（accuracy）度量

覆盖率（coverage）：满足规则前件的记录所占比例
规则的精度（Accuracy of a rule）：触发r的记录中类标号等于y的记录所占的比例

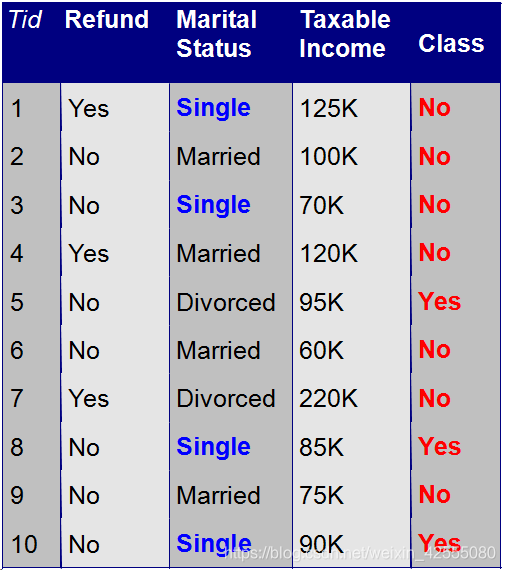
如下图的覆盖率和准确率为：
Rule: (Status=Single) —> No
Coverage = 40%, Accuracy = 50%

三规则的分类器的特征

互斥规则（Mutually exclusive rules）
- 每个记录最多被一个规则覆盖
- 如果规则集中不存在两条规则被同一条记录触发，称规则集中的规则是互斥的
- 如果规则集不是互斥的:一个记录可能触发多条规则
  解决办法：
  - 有序规则集（Ordered rule set）
    基于规则的排序方案、基于类的排序方案
  - 无序规则集（ Unordered rule set）
    使用投票模式
穷举规则（Exhaustive rules）
- 如果对属性值的任一组合，都存在一条规则加以覆盖，成规则集具有穷举覆盖
  确保了每一条记录都至少被一条规则覆盖
- 如果规则不是穷举的:一条记录可能不会触发任何规则
  解决办法：
  - 使用缺省类（即通常被指定为没有被现存规则覆盖的训练记录的多数类）

3.1 有序规则集

规则集中规则按照优先级的降序排列(优先级可以基于准确率、覆盖率、总描述长度、规则产生的顺序等）
有序的规则集称为决策表（ decision list）
当一个测试记录出现时
该记录的类标号由它触发的最高优先级的规则决定，这就避免了预测类冲突的问题
如果没有命中任何规则，记录的类标号为缺省类
在这里插入图片描述

3.2 规则的排序方案

基于规则的排序（Rule-based ordering）
依据规则的质量的某种度量对规则排序（确保每个测试记录都是由覆盖它的最好的规则类分类）
缺点：每个规则都假设排在它前面的规则不成立，规则量大时，解释后面规则麻烦）
基于类的排序（Class-based ordering）
属于同一个类的规则在规则集中一起出现，根据它们所属的类信息一起排序
同一个类的规则的相对顺序不重要，只要触发一个规则，就赋予测试记录类标号
缺点：科恩那个导致高质量的规则被忽略

四如何建立基于规则的分类器

直接方法（Direct Method）:
直接从数据中提取分类规则
把属性空间分为较小的子空间，以便于属于一个子空间的所有巨鹿可以使用一个分类规则进行分类
例如: RIPPER, CN2, Holte’s 1R
间接方法（Indirect Method）:
从其他分类模型（如决策树和神经网络）中提取分类规则.
使用分类规则为较复杂的分类模型提供简介的描述
例如: C4.5 rules

说明：著名的基于规则的分类器都采用基于类的排序方案，如C4.5，PIPPER

4.1 规则提取的直接方法—顺序覆盖算法

顺序覆盖算法经常被用来从直接数据中提取规则，规则基于某种评估度量以贪心的方式增长。该算法从包含多个类的数据集中一次提取一个类的规则。决定哪一个类的规则最先产生的标准取决于多种因素，如类的普遍性（即训练记录中属于特定类的记录的比例），或者给定类中误分类记录的代价。
基本思想：
开始决策表为空，用留一规则提取类y的覆盖当前训练记录集的最佳规则。在提取规则时，类y的所有训练记录被看作正例，而其他类的训练记录看作反例。如果一个规则覆盖大多数正例，那么该规则是可取的，这时删除它所覆盖的训练记录，把新规则追加到决策表中。重复这个过程直到满足终止条件
　

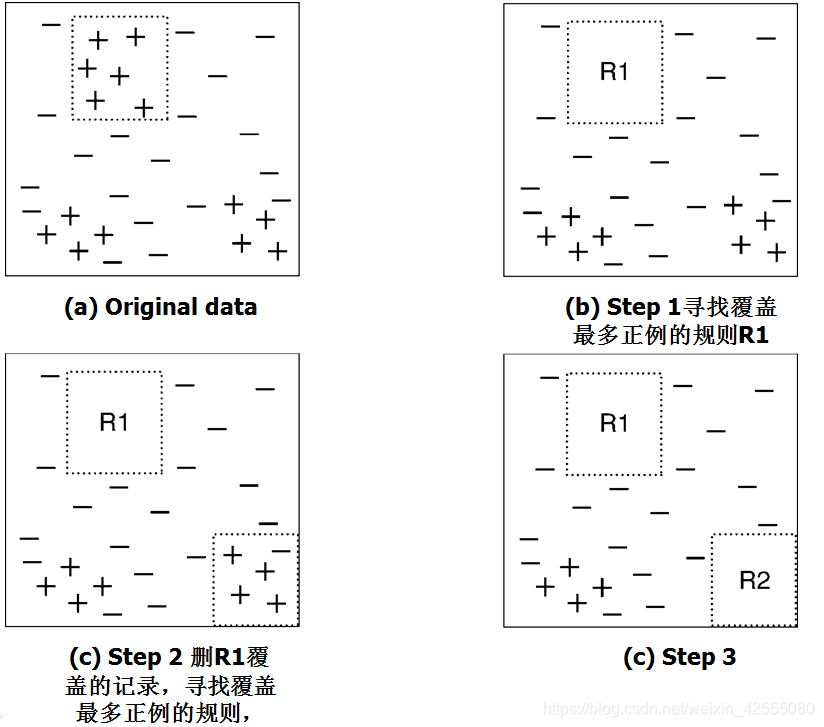
如下图演示在包含一组正例和反例的数据集上顺序覆盖算法是怎样工作的。规则R1，其覆盖如（b）所示，首先被提取出来，因为它覆盖的正例最多。接下来去掉R1覆盖的所有训练记录，算法继续寻找下一个最好的规则，即R2。
在这里插入图片描述

4.1.1 Learn-One-Rule函数

Learn-One-Rule函数的目标是提取一个分类规则，该规则覆盖训练集中的大量正例，没有或仅覆盖少量反例。然而，由于搜索空间呈指数大小，要找到一个最佳的规则的计算开销很大。Learn-One-Rule函数通过以一种贪心的方式的增长规则来解决指数搜索问题。它产生一个初始规则r，并不断对该规则求精，直到满足某种终止条件为止。然后修剪该规则，以改进它的泛化误差。

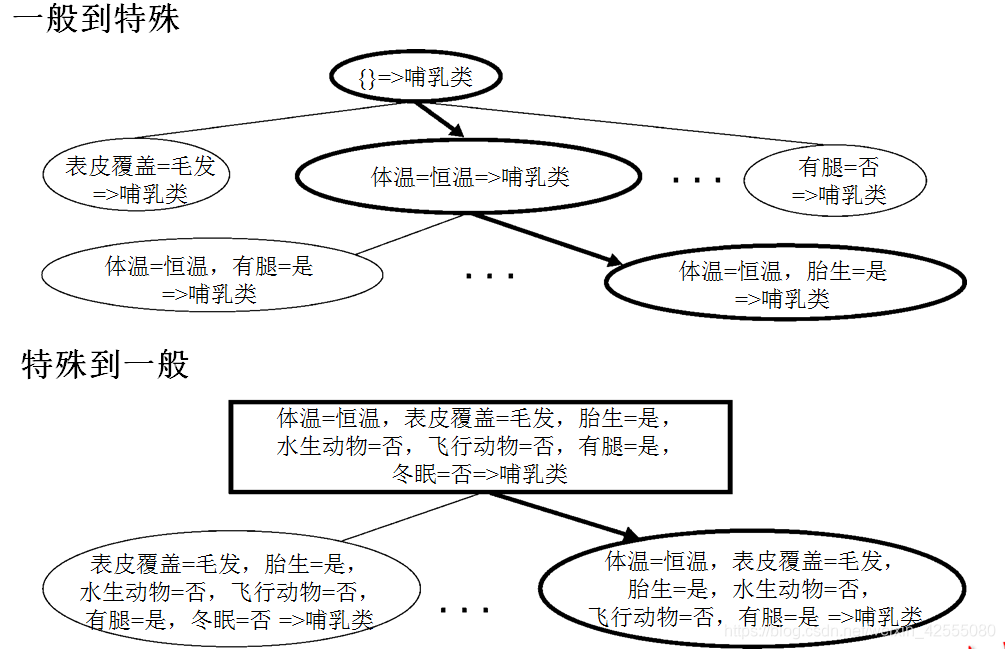
规则增长策略 常见的分类规则增长策略有两种：从一般到特殊和从特殊到一般。

在从一般到特殊的策略中，先建立一个初始规则r:{}→y，其中左边是一个空集，右边包含目标类。该规则的质量很差，因为它覆盖训练集中的所有样例。接着加入新的合取项来提高规则的质量，直到满足终止条件为止（例如，加入的合取项已不能提高规则的质量）
对于从特殊到一般的策略，可以随机地选择一个正例作为规则增长的初始种子。再求精步，通过删除规则的一个合取项，使其覆盖更多的正例来范化规则。重复求精步，直到满足终止条件为止（例如，当规则开始覆盖反例时为止）。

由于规则的贪心的方式增长，以上方法可能会产生次优规则。为了避免这种问题，可以采用束状搜索（beam search）。算法维护k个最佳候选规则，各候选规则各自在其前件中添加或删除合取项而独立地增长。评估候选规则的质量，选出k个最佳候选进入下一轮迭代。
　

规则评估 在规则的增长过程中，需要一种评估度量来确定应该添加（或删除）哪个合取项。准确率就是一个很明显的选择，因为它明确地给出了被规则正确分类的训练样例的比例。然而把准确率作为标准的一个潜在的局限性是它没有考虑规则的覆盖率。例如，考虑一个训练集，它包含60个正例和100个反例。假设有如下两个候选规则：

规则r1：覆盖50个正例和5个反例，
规则r2：覆盖2个正例和0个反例。

r1和r2的准确分别为90.9%和100%。然而，r1是较好的规则，尽管其准确率较低。r2的高准确率具有潜在的欺骗性，因为他的覆盖率太低了。

下面的方法可以用来处理该问题。

（1）可以使用统计检验剪除覆盖率较低的规则。例如，我们可以计算下面的似然比（likelihood ratio）统计量：
　

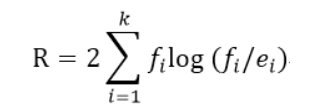
其中，k是类的个数，fi 是被规则覆盖的类i的样本的观测频率，ei 是规则作随机猜想的期望频率。注意R是满足自由度为k-1的χ2分布。较大的R值说明该规则做出的正确预测数显著地大于随机猜测的结果。
　

（2）可以使用一种考虑规则覆盖率的评估度量。考虑如下评估度量：
　

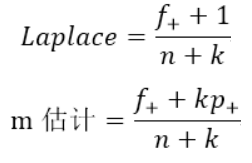
其中n是规则覆盖的样例数，f+是规则覆盖的正例数，k是类的总数，p+是正类的先验概率。注意当p+=1/k时，m估计等价于Laplace度量。
（3）另一种可以使用的评估度量是考虑规则的支持度计数的评估度量。FOIL信息增益就是一种这样的度量。规则的支持度计数对应于它所覆盖的正例数。假设规则r : A→+覆盖p0个正例和n0个反例。增加新的合取项B，扩展后的规则r’ : A∧B→+覆盖p1个正例和n1个反例。根据以上信息，扩展后规则的FOIL信息增益定义为：
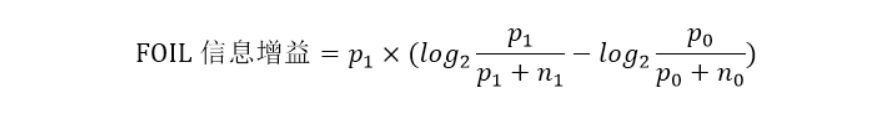
在这里插入图片描述
由于该度量与p1和p1/p1+n1成正比，因此它更倾向于选择那些高支持度计数和高准确率的规则。

规则减枝 可以对Learn-One-Rule函数产生的规则进行减枝，以改善它们的泛化误差。

4.1.2 顺序覆盖基本原理

规则提取出来后，顺序覆盖算法必须删除该规则该规则所覆盖的所有正例和反例。
　

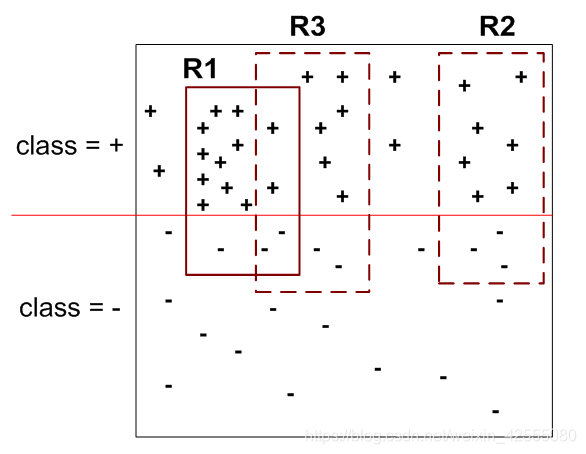
上图中有29个正例，21个反例，R1,R2,R3三个规则的准确率分别为12/15, 7/10, 8/12。

R1先产生，因为它的准确率最高。R1产生后，很明显要删除它所覆盖的所有正例，以便算法产生的下一条规则不同于R1。（为什么要删除记录?不删除，下一个规则会和上一个产生的规则相同）
下一步,假设算法可以产生R2和R3。尽管R2的准确率比R3高，但是R1和R3起覆盖了18个正例和5个反例(总体准确率达到78.3%),而R1和R2一起覆盖了19个正例和6个反例(总体准确率只有76%)。如果在计算准确率之前就删除R1所覆盖的正例和反例，那么R2或R3对准确率的这种增量影响就会更明显。特别地，如果不删除R1所覆盖的正例，那么我们就会高估R3的准确率;如果不删除R1所覆盖的反例，则会低估R3的准确率。在后一种情况下，我们最终可能会选择规则R2，尽管R3所造成的虚假正例误差有一半已经被先前的规则R1所解决。

4.1.3 RIPPER算法

为了阐明规则提取的直接方法，考虑一种广泛使用的规则归纳算法，叫作RIPPER算法。该算法的复杂度几乎线性地随训练样例的数目增长，并且特别适合为类分布不平衡的数据集建立模型。RIPPER也能很好地处理噪声数据集，因为它使用一个确认数据集来防止模型过分拟合。

对两类问题，RIPPER算法选择以多数类作为默认类，并为预测少数类学习规则。对于多类问题，先按类的频率对类进行排序，设（y1,y2,…,yc）是排序后的类，其中y1是最不频繁的类，yc是最频繁的类。第一次迭代中，把属于y1的样例标记为正例，而把其他类的样例标记为反例，使用顺序覆盖算法产生区分正例和反例的规则。接下来，RIPPER提取区分y2和其他类的规则。重复该过程，直到剩下类yc，此时yc作为默认类。

规则增长 RIPPER算法使用从一般到特殊的策略进行规则增长，使用FOIL信息增益来选择最佳合取项添加到规则前件中。当规则开始覆盖反例时，停止添加合取项。新规则根据其在确认集上的性能进行减枝。计算下面的度量来确定规则是否需要减枝：(p-n)/(p+n)，其中p和n分别是被规则覆盖的确认集中的正例和反例数目，关于规则在确认集上的准确率，该度量是单调的。如果减枝后该度量增加，那么就去掉该合取项。减枝是从最后添加的合取项开始的。例如给定规则ABCD→y，RIPPER算法先检查D是否应该减枝，然后是CD、BCD等。尽管原来的规则仅覆盖正例，但是减枝后的规则可能会覆盖训练集中的一些反例。

建立规则集 规则生成后，它所覆盖的所有正例和反例都要被删除。只要该规则不违反基于最小描述长度的终止条件，就把它添加到规则集中。如果新规则把规则集的总描述长度增加了至少d个比特位，那么RIPPER就停止把该规则加入到规则集（默认的d是64位）。RIPPER使用的另一个终止条件是规则在确认集上的错误率不超过50%。

RIPPER算法也采用其他的优化步骤来决定规则集中现存的某些规则能否被更好的规则替代。

4.2 规则提取的间接方法

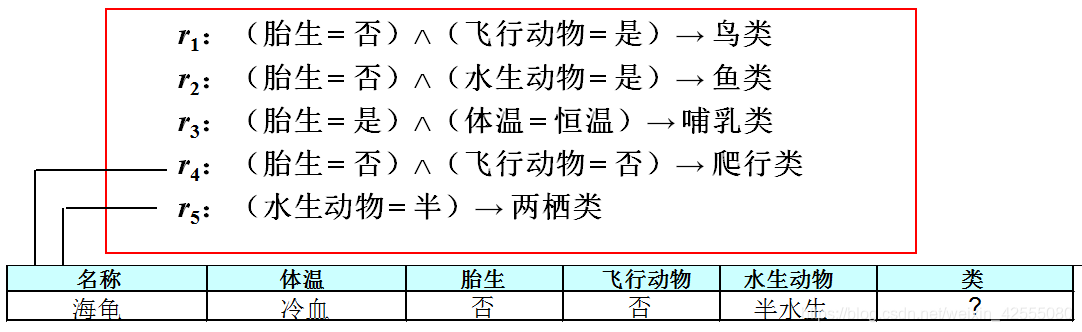
这是一种由决策树生成规则集的方法。原则上，决策树从根节点到叶节点的每一条路径都可以表示为一个分类规则。路径中的测试条件构成规则前件的合取项，叶节点的类标号赋给规则后件。注意，规则集是完全的，包含的规则是互斥的。但是，下面这个例子中的某些规则是可以简化：
　

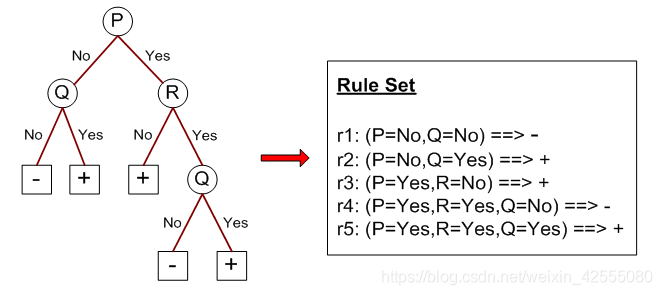
说明：r2,r3可以简化：
r2: (Q=Yes)→+
r3: (P=Yes)^(R=No) →+

下面，介绍C4.5规则算法所采用的从决策树生成规则集的方法。
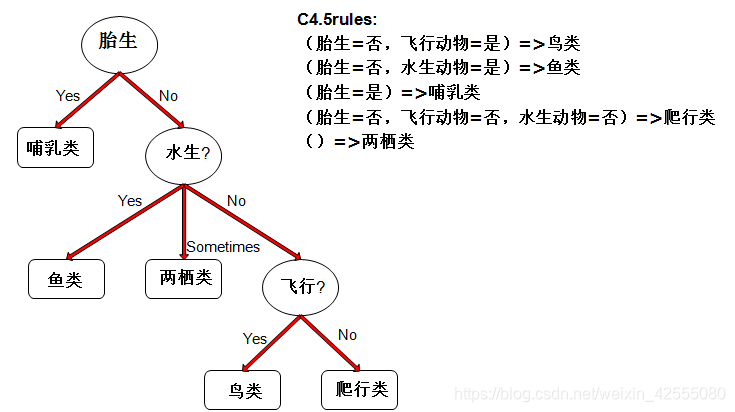
在这里插入图片描述
规则产生 决策树中从根节点到叶节点的每一条路径都产生一条分类规则。给定一个分类规则r : A→y，考虑简化后的规则 r’: A’ →y，其中A’是从A去掉一个合取项后得到的。只要简化后的规则的误差率低于原规则的误差率，就保留其中悲观误差率最低的规则。重复规则减枝步骤，直到规则的悲观误差不能再改进为止。由于某些规则在减枝后会变得相同，因此必须丢弃重复规则。
规则排序 产生规则集后，C4.5规则算法使用基于类的排序方案对提取的规则定序。预测同一个类的规则分到同一个子集中。计算每个子集的总描述长度，然后各类按照总描述长度由小到大排序。具有最小描述长度的类优先级最高，因为期望它包含最好的规则集。类的总描述长度等于Lexception+g×Lmodel，其中Lexception是对误分类样例编码所需的比特位数，Lmodel是对模型编码所需要的比特位数，而g是调节参数，默认值为0.5,。调节参数的值取决于模型中冗余属性的数量，如果模型含有很多冗余属性，那么调节参数的值会很小。

五总结

基于规则的分类器有如下特点：

规则集的表达能力几乎等价于决策树，因为决策树可以用互斥和穷举的规则集表示。基于规则分类器和决策树分类器都对属性空间进行直线划分，并将类指派到每个划分。然而，如果基于规则的分类器允许一条记录触发多条规则的话，就可以构造一个更加复杂的决策边界。
基于规则的分类器通常被用来产生更易于解释的描述性模型，而模型的性能却可与决策树分类器相媲美。
被很多基于规则的分类器（如RIPPER）所采用的基于类的规则定序方法非常适于处理类分布不平衡的数据集。

这篇文章就到这里了，欢迎大佬们多批评指正，也欢迎大家积极评论多多交流。
　