一、基本概念

基本思想是将数据关联问题转换为图，计算最稠密的全连接子图，具体描述有点拗口：

1、图的节点是什么

假设有两组数据setA和setB，setA有a,b,c,d,e这几个点，setB里面有i,j,k,l这个几个点。
如果认为setA中的某个点a和setB中的某个点j能匹配，setA中的另一个点c和setB中的另一个点l能匹配，那么a-c的相对关系和j-l的相对关系应该是一致的。这个相对关系可以自己设计。这个也很好理解。
这个思路，其实也是所谓的geometry consistency检查的内容。比如orbslam中多次去检测连续几帧的特征点能连续的被匹配到，数量有一定的要求。其实orbslam里不是很严格的几何一致性检测，只是基于概率上来说，不是的概率已经很低了。

看一下论文里面的示意图：
在这里插入图片描述

2、怎么找最稠密的子图

其实以上的思路，自己用过，但是没有进行进一步的处理，提取成为一个最大全联通子图的问题，更没有想到后面的优化。
当时是找到匹配后，找一个点和另一个点计算相对关系，把另一组中的点对也找出来，计算相对关系，然后比较两个相对关系的相似度，满足条件就认为多一个支持度，大概计算一下谁的支持度最多。

重点是理解优化的思路，这个怎么就能够通过优化计算出来了。如果是原始的方法，这个计算，就是一个n的n次方的时间复杂度，可想而知，不太可能在实际中被使用。大概就是这么个结构：

forfor for....

二、关于优化目标

1 先看看最原始的目标

在这里插入图片描述

u是我们的优化目标。我们能不能令u的所有元素都是1呢？不能，因为subject to决定了，如果M(i,j)=0，那么对应ui和uj只能有一个为1 。
原始的找出最优的u向量的值，还是一个 $n^n$ 的复杂度。

上面的问题，如果M是一个二值矩阵，则可以转换为下面的优化目标：
在这里插入图片描述

因为ui不能都取1，所以上面（2）的优化也是有意义的，很明显就是我们要找的。这个问题又等价于MCP问题。上面的文字还解析了为什么能正确的找出来，是因为假设噪声数据都是无序无规律，不会有系统性偏差的，所以相对关系就是一个随机数，而正确关联的数据，其相对关系都是比较一致的。
上面也解析了MCP是一个NP-hard的问题。不能硬解。

但是，说起来，M这个矩阵并不是一个0，1矩阵，而是内部是浮点数，这个也好理解，不是每次观测都是完美的，两个东西，在两次观测中的相对位置会有所变动是有可能的，所以，需要一个相似度来去衡量。为1的话当然好，那就是完全相似，那不是很相似，又有点相似，就需要一个值来去衡量了，看第一个示意图，用两种相似度的衡量，那个矩形框r(x)就是0或者1，而高斯分布的曲线s(x)就是对相似度有一个具体的分辨，一般这个是我们要的。

论文后面说到，公式（2）不是目标，而是需要将M考虑进去。
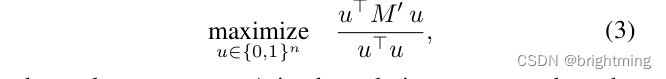
在这里插入图片描述

2 怎么进一步分析这个优化目标

解决（1）的主要挑战在于问题的组合复杂性，这是由于其二进制域和u的非线性目标所导致的。这使得在实时环境中以全局最优的方式解决问题变得困难，即使对于小规模的数据关联问题也是如此。一个常见的解决方法是放松（1）的域和约束，得到一个连续的问题，便于快速求解，然后将该解投影回原问题的域和约束流形。在可以考虑的放松策略中，以下方法的主要优势是从放松问题中获得的解与原问题的最优解相对应，很快将会讨论。
就是这个：
在这里插入图片描述

与（1）的区别是什么呢？M矩阵，原来是0的地方，填上了一个负数，来表示惩罚，比如同时选择ui和uj，那么总分就会被惩罚降低下来。而且这个惩罚是2倍的uiujd，就是uiujd+ujuid。把subject to的给集成进去一起考虑了。确实是高明。
关键来了：“因此，随着 d 的增加，违反约束条件的解 u 的元素被推向零。”

“当 d ≥ n 时，(5)的（局部或全局）最优解满足原始问题中的约束，即如果 M(i, j) = 0，则 u_i * u_j = 0。这个事实已经在[18]中针对 M 为二进制矩阵的情况下进行了证明。虽然我们已经将证明扩展到了加权情况，但这个讨论超出了本文的篇幅限制，将在随后的期刊投稿中呈现。我们指出，由于（1）是一个NP难题，根据初始条件，用于解决（5）的优化算法可能会收敛到局部最优解。为了保证找到全局最优解，需要搜索整个解空间。”

“给定满足 d ≥ n 的（5）的解 u，设 G0 ⊆ G 表示对应于 u 的非零元素的子图，并且 M0 是对应于 G0 的 M 的子矩阵。注意到 u，因此 G0，在（1）中满足约束条件，问题（1）可以简化为将 u 二值化，使目标最大化。这等价于（3）中的最密子图问题，其目标是找到具有最大密度的 G00 ⊆ G0。最密子图问题可以使用现有的算法[26]在多项式时间内解决，但通过选择 u > Mu 的 ω̂ = round(u > Mu) 最大元素作为 G00 的顶点，可以立即获得一个很好的近似答案。这个解决方法的合理性可以从以下众所周知的事实得到解释：u > Mu，即 G0 的谱半径，是图的密度的紧密上界[27]，而 u 的非零元素，即 M0 的主特征向量，代表其对应顶点的中心性，这是图中顶点连通性的度量[28]。” 这一段话涉及到谱图，理解不了了。

待续。。。。