蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术

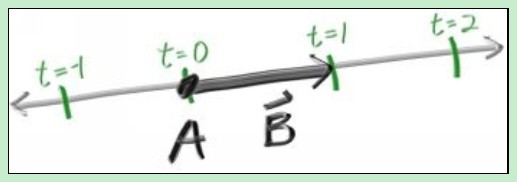
所有光线跟踪器都有一个光线类，以及计算沿光线看到的颜色。让我们把射线看作一个函数，p(t)=A+t*B，这里p是3D中沿直线的3D位置，a是射线的原点，B是射线的方向。射线参数t是实数（代码中的浮点数）。插入不同的t和p(t)沿射线移动点。

加上负t，你就可以得到3D线上的任何地方。对于正t，你只得到A前面的部分，这就是通常所说的半线或射线。示例C=p(2)如下所示：

现在我们准备好转弯，做一个光线跟踪器。光线跟踪器的核心是通过像素发送光线，并计算在光线方向上看到的颜色。它的形式是计算从眼睛到像素的光线，计算光线与像素相交的部分，并计算该相交点的颜色。在第一次开发光线跟踪器时，我总是用一个简单的相机来启动和运行代码。我还做了一个简单的颜色（光线）函数，返回背景的颜色（一个简单的渐变）。

我经常在使用正方形图像进行调试时遇到麻烦，因为我经常转换x和y，所以我将坚持使用200x100图像（这里我还是用的512*512的图像）。我将把“眼睛”（或者相机中心，如果你想到相机的话）设为（0,0,0）。我让y轴向上，x轴向右。为了尊重右手坐标系的对流，进入屏幕的是负z轴。我将从左下角遍历屏幕，并使用沿屏幕边的两个偏移向量来移动屏幕上的光线端点。请注意，我没有将光线方向设置为单位长度向量，因为我认为不这样做会使代码更简单、速度略快。

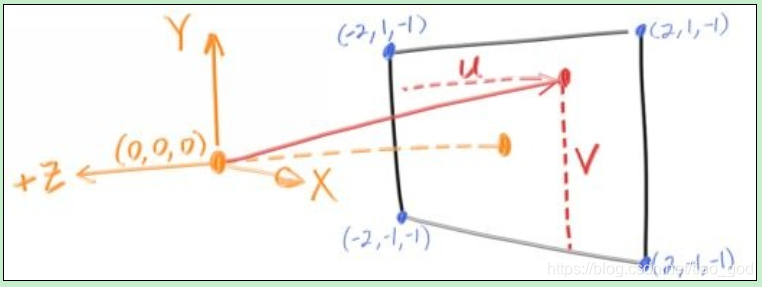
在下面的代码中，光线r接近像素中心（我现在不担心精确性，因为我们稍后将添加抗锯齿）：

#ifndef RAY_H
#define RAY_H#include "Vector3.h"class Ray  {
public:Ray() {}Ray(const Vector3& a, const Vector3& b) { data[0] = a; data[1] = b; data[2] = Vector3(1.0f / b.x(), 1.0f / b.y(), 1.0f / b.z());posneg[0] =  (data[1].x() > 0 ? 0 : 1);posneg[1] = posneg[0] ^ 1;posneg[2] =  (data[1].y() > 0 ? 0 : 1);posneg[3] = posneg[2] ^ 1;  posneg[4] =  (data[1].z() > 0 ? 0 : 1);posneg[5] = posneg[4] ^ 1;  }Ray(const Ray& r) {*this = r;}Vector3 origin() const {return data[0];}Vector3 direction() const {return data[1];}Vector3 invDirection() const {return data[2];}void setOrigin(const Vector3& v) {data[0] = v;}void setDirection(const Vector3& v) {data[1] = v;data[2] = Vector3(1.0f / v.x(), 1.0f / v.y(), 1.0f / v.z());posneg[0] =  (data[1].x() > 0 ? 0 : 1);posneg[1] = posneg[0] ^ 1;posneg[2] =  (data[1].y() > 0 ? 0 : 1);posneg[3] = posneg[2] ^ 1;  posneg[4] =  (data[1].z() > 0 ? 0 : 1);posneg[5] = posneg[4] ^ 1;  }Vector3 pointAtParameter(float t) const { return data[0] + t*data[1]; }Vector3 data[3];int posneg[6]; 
};#endif

写个程序测试一下：

	Vector3 lower_left_corner(-2.0, -1.0, -1.0);Vector3 horizontal(4.0,0.0,0.0);Vector3 vertical(0.0,2.0,0.0);Vector3 origin(0.0, 0.0, 0.0);for (int j = HEIGHT-1;j >= 0;j--) {for (int i = 0;i < WIDTH;i++) {int offset = (WIDTH*i + j) * 4;float u = float(i) / float(WIDTH);float v = float(j) / float(HEIGHT);Ray r(origin, lower_left_corner+u*horizontal+v*vertical);Vector3 col((u-0.5)*(u-0.5)+(v-0.5)*(v-0.5),0.0,0.0);Pixels[offset + 0] = (unsigned char)255.99*col[0];Pixels[offset + 1] = (unsigned char)255.99*col[1];Pixels[offset + 2] = (unsigned char)255.99*col[2];Pixels[offset + 3] = 255;}}

得到效果如图：