1. 构造决策树
1.1 构造思路
首先,构造决策树的过程如下:
① 按特征划分群体,并计算衡量指标(信息增益、信息增益率、基尼系数)
② 选取衡量指标表现最好的特征,对群体进行划分,并构建第一层树
③ 重复①②步骤,当特征全被分完,或是类别唯一确定后,停止划分(还可以是其他条件)
1.2 构造困惑
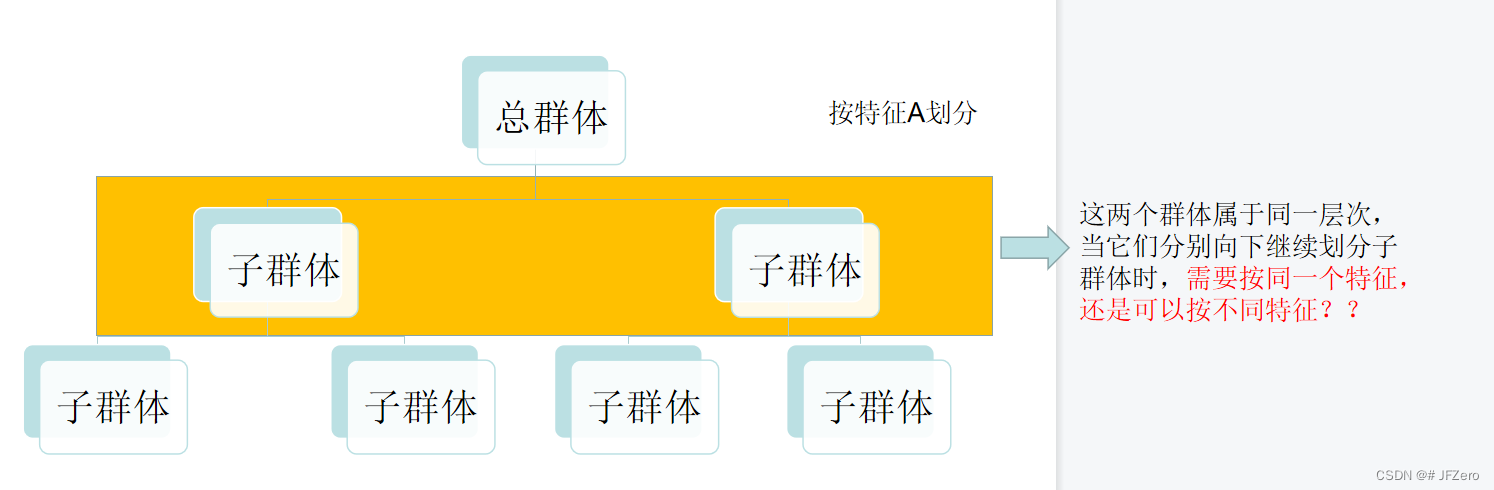
在思考构造决策树的时候,我忽然有个问题:同一个层级的不同群体,需要继续向下划分出各自的子群体时,是按相同的特征划分,还是按照各自的条件熵最大那个特征来分?
尝试想了想同一层级的群体按相同特征,继续向下划分时,这个衡量的指标就要层层嵌套为条件熵的加权平均值。。。而且划分的层级越多,例如4个层级,那衡量的指标就要变为条件熵的加权平均条件熵的加权平均条件熵的加权平均条件熵…、、
尽可能地让整颗决策树的划分更纯
forget about it
套娃的路子,可以走,但没这必要
还是直接根据“贪心算法”的思路,走好这一步,再走好下一步,每一步都走好了,那总体也是好的
【在一定情况下,但有时候贪心算法并不能达到全局最优,无所谓,至少比乱走的好】
1.3 程序设计的难点
- 用什么数据结构来设计决策树?存储划分的群体?
👉选取二叉树,显然是不行的,因为在决策树中特征值是应分尽分,不同特征有不同数量的特征值,因此二叉树只有左右两个叉,不适用
👉选取字典,目测应该是可以的,但考虑要迭代递归去逐级划分,可以考虑多叉树
多叉树这个东西呢…属实是自己乱来了,但实践后发现其实还挺好用的
我并不是一开始就把所有的结构都想的十分清楚明白,只是大概画了个草图设计了一下,纪念一下我的草图
鬼都看不懂的草图,我自己现在也不知道当时是怎么想的
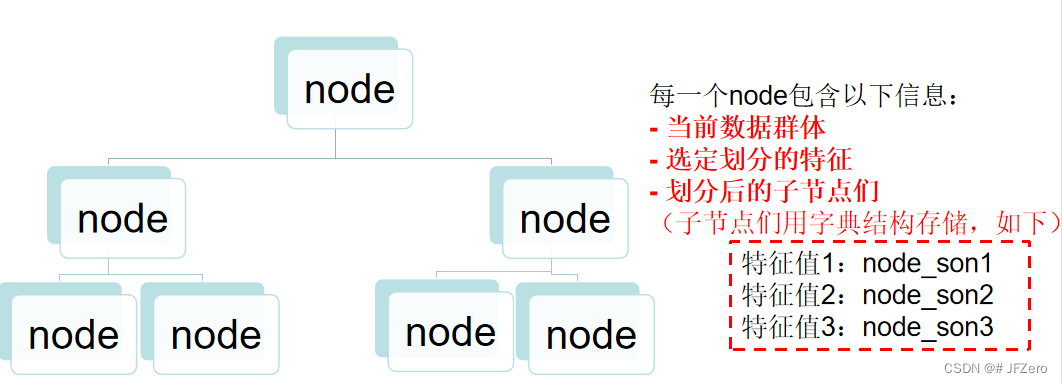
实际最后设计出的多叉树结构大致如下
1.4 手动代码
import math
import numpy as np
import pandas as pd
# 获取所需数据
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐类型','推荐分值', '专业度','回复速度']
datas_1 = datas[important_features]
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)
Y_feature = "推荐类型"# 构建一个树节点
class Node_1():def __init__(self,value):self.value = valueself.select_feat = Noneself.sons = {}
# 根据节点,构建一个树
class Tree():def __init__(self):self.root = Nonedef get_value_1(self,datas_arg,node_arg=None):# 明确当前节点数据node = node_argif self.root == None:node = Node_1(datas_arg)self.root = node# 明确当前节点的划分特征、子节点们: 计算各特征划分后的信息增益,并选出信息增益最大的特征gain_dicts = {}for i in X.columns:groups = datas_arg.groupby(i)groups = [groups.get_group(j) for j in set(datas_arg[i])]if len(groups) > 1: # 特征可分gain_dicts[i] = self.get_gain(datas_arg,groups,Y_feature)# 明确停止划分的条件,即停止迭代的条件:无可划分的属性,或是最大的条件熵为0if (not gain_dicts) or max(gain_dicts.values()) == 0:returnselect_feat = max(gain_dicts,key=lambda x:gain_dicts[x])node.select_feat = select_featgroup_feat = datas_arg.groupby(select_feat)for j in set(datas_arg[select_feat]):node_son_value = group_feat.get_group(j)node_son = Node_1(node_son_value)node.sons[j] = node_sonfor key,node_single in node.sons.items():self.get_value_1(node_single.value,node_single)# 获取熵def get_ent(self,datas,feature):p_values = datas[feature].value_counts(normalize=True)p_updown = 1/p_valuesent = (p_values*(p_updown).apply(np.log2)).sum()return ent# 获取条件熵def get_condition_ent(self,datas_list,feature):proportions = [len(i) for i in datas_list]proportions = [i/sum(proportions) for i in proportions]ents = [self.get_ent(i,feature) for i in datas_list]condition_ent = np.multiply(ents,proportions).sum()return condition_ent# 获取信息增益def get_gain(self,datas_all,datas_group,feature):condition_ent = self.get_condition_ent(datas_group,feature)ent_all = self.get_ent(datas_all,feature)gain = ent_all - condition_entreturn gain# 探访决策树,并进行预测分类def predict(self,data,root):if not root.select_feat:p_values = root.value[Y_feature].value_counts(normalize=True)Y_predict.append(p_values.idxmax())returnfeat = root.select_featnext_node = root.sons[data[feat]]self.predict(data,next_node)def pre_print(self, root):if root is None:returnprint(root.select_feat)print(root.value)for key,node_son in root.sons.items():self.pre_print(node_son)a = Tree()
a.get_value_1(datas_1)
Y_predict = []
def func(data):a.predict(data,a.root)datas_1.apply(func,axis=1)
accurency = sum(Y_predict==Y)/len(Y)
print(f"分类准确率:{accurency*100}%")
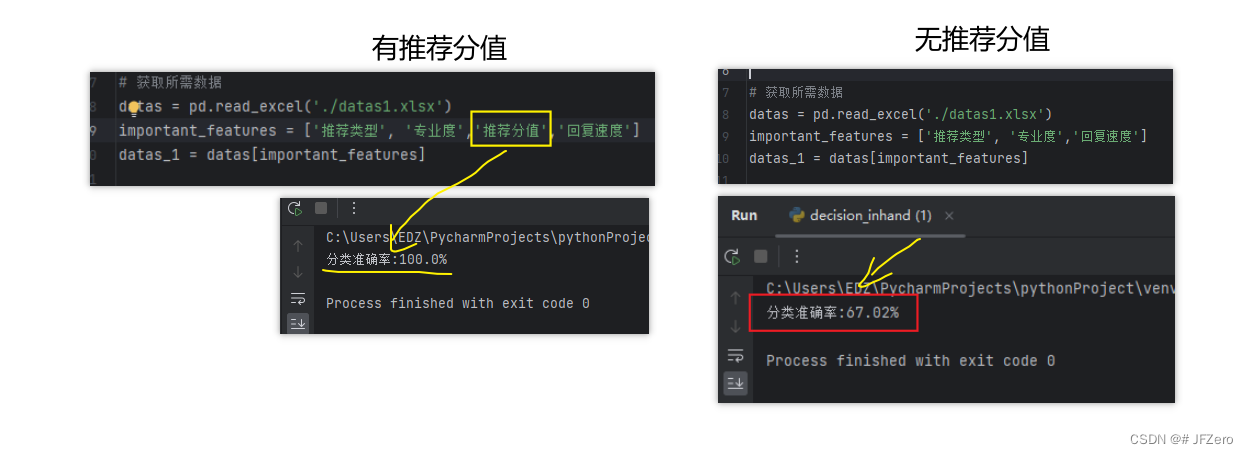
总体表现还不错,有推荐分值的情况下,推荐类型会是百分百的正确
没有推荐分值的情况下,推荐类型勉强还可以【跟朴素贝叶斯差不多】
2. 剪枝
没做剪枝…懒得
当即使分到的决策树,没有达到分类最纯粹的状态也没关系,可以直接按叶子节点的类别概率来预测分类
但是不剪枝会不会对条件熵的计算有影响呢?
这倒是没考量过,maybe,无所谓啦
以后遇到需要真的剪枝了,再剪吧