前面提到过一个 AIMD 的修正方法,“二次机会 MD”:首次丢包只 MD 收缩一个相对较小的比例,再次丢包时再继续收缩,直到 beta * Wmax。
效果如下图:
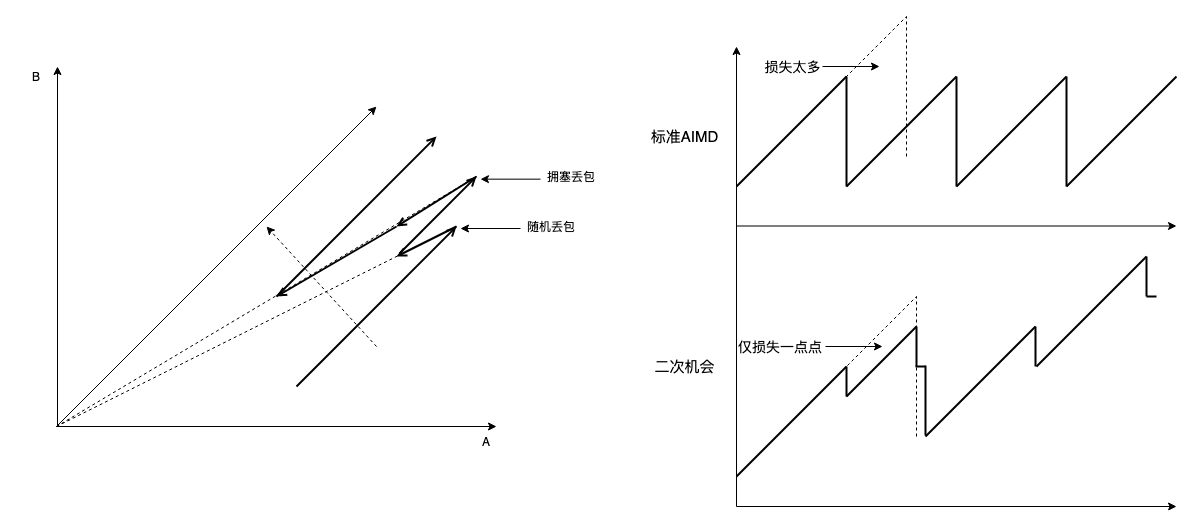
大意是在检测到丢包时,先 MD 一个相对小的缩放比例,如果再次丢包再继续缩放,由此可在不损害公平性(cc 只为拥塞才会降速收敛,随机丢包本来就不应该降速)的前提下抵抗随机丢包:如果随机丢包,由于缩放系数较小,带宽损失不大,cwnd 可从相对高的位置开始描绘 cwnd/time 曲线,如下图所示:

如果真拥塞,PRR 过程的发送线将变成一条上凸曲线(线 2),逐渐弯下去,最终和标准 PRR 的结果相汇。虽 “有悖于 PRR” 按比例收敛到 0.7 * Wmax,但减速收敛到 0.7 * Wmax 也没什么不好。
做这个修改一开始就是想让 MD 过程也呈现一条曲线而不是一条直线,就像 AI 过程一样,收敛到结果,而非过程。减速收敛显然可以抗随机丢包,在随机丢包后不至于下降太多,但代价是真拥塞时响应没有标准 PRR 过程快,不过即使标准 PRR 不是论证的结果。
简单写了个代码:https://github.com/marywangran/tcp_cubic_v2
虽然二次机会 MD 算法可以抵抗明确的随机丢包,但随机丢包太频繁的话也扛不住,大概就是积累 AI 和 MD 总量持平或更小的时候,由于没有足够的数据量进行 probe,有效吞吐将明显下跌。但凡 probe 都需要超过有效 BDP 的数据量做支撑,因此在小 buffer 链路,probe 本身也会造成 buffer 溢出而丢包,如 BBR 代码的 probe 注释所说:We do not persist if packets are lost, since a path with small buffers may not hold that much。
和 BBR 抗丢包相比,它那个是憋住 maxbw 守恒观望,我这个是损失一点点代价赌能跨过去。BBR 像是油门踩到底跨过随机丢包,我这个像轻踩刹车。
AIMD 公平性很重要,否则大可使用别的 “更好” 的算法,AIMD 的核心就是收敛到公平。任何魔改都不要破坏这一点。AIMD 的公平收敛其实就是一个勾兑的过程,一杯葡萄汁液:橙汁为 3:1 的混合液体,如何勾兑成 2:1,就是 AIMD:先加入 1:1 液体一小勺,这就是 AI,均匀混合后舀出去相同的量,舀出去的液体中二者的比例很容易计算,这就是 MD,重复这个过程 n 次即可,数学上很容易计算 n。
为判断随机丢包,不要引入过于复杂的逻辑,ACK 时钟信息量有限,判断精度必有上限,类似于硬币猜正反,因为你的信息就那么多,50% 的概率,那就随机猜即最优解,不要启发。丢包判断也一样,别做假设,一旦误判就要为负方向买单,这是信息论决定的。
通用场景,不做假设,最简单最好。我们都明白,特定场景优化很容易,这相当于事前已经告诉你要做什么,但问题是当这个 “特定场景” 混杂在通用场景中时,很难将其识别出来,这才是最难的问题,这个问题无解,结果就是拆了东墙补西墙,统计意义上看跟没有优化一样。
上周那个 “二次机会 AIMD” 跟朋友介绍了一下,挺不错,本来不到 5 分钟就能改一版 cubic ++,结果还是因为 Linux tcp 开放的 cc 模块受制于拥塞状态机,我若实现脱缰的 cong_control 回调,就要亲自调用 PRR,不过还算简单,吃点烧烤的工夫就能写完。相比 ns-3 写模拟,我还是倾向于直接写 Linux 模块的 cong_control 回调。
浙江温州皮鞋湿,下雨进水不会胖。