【ELMAN回归预测】基于matlab天牛须算法优化ELMAN回归预测【含Matlab源码 1375期】

⛄一、天牛须搜索算法简介

1 天牛须搜索算法定义
天牛须搜索（Beetle Antennae Search-BAS），也叫甲壳虫须搜索，是2017年提出的一种高效的智能优化算法。类似于遗传算法、粒子群算法、模拟退火等智能优化算法，天牛须搜索不需要知道函数的具体形式，不要虚梯度信息，就可以实现高效寻优。相比于粒子群算法，天牛须搜索只只要一个个体，即一个天牛，运算量大大降低。

2 原理及代码实现
2.1 仿生原理
天牛须搜索时受到天牛觅食原理启发而开发的算法。
生物原理：当天牛觅食时，天牛并不知道食物在哪，而是根据食物气味的强弱来觅食。天牛有俩只长触角，如果左边触角收到的气味强度比右边大，那下一步天牛就往左飞，否则就往右飞。根据这一简单原理天牛就可以有效找到食物。
天牛须搜索得来的启发：食物的气味就相当于一个函数，这个函数在三维空间每个点值都不同，天牛两个须可以采集自身附近两点的气味值，天牛的目的是找到全局气味值最大的点。仿照天牛的行为，我们就可以高效的进行函数寻优。

2.2 算法
天牛在三维空间运动，而天牛须搜索需要对任意维函数都有效才可以。因而，天牛须搜索是对天牛生物行为在任意维空间的推广。采用如下的简化模型假设描述天牛：
天牛左右两须位于质心两边。
天牛步长step与两须之间距离d0的比是个固定常数，即step=c*d0，其中c是常数。即，大天牛（两须距离长）走大步，小天牛走小步。
天牛飞到下一步后，头的朝向是随机的。

2.3 建模：（n维空间函数f最小化）
第一步：对一个n维空间的优化问题，我们用xl表示左须坐标，xr表示右须坐标，x表示质心坐标，用d0表示两须之间的距离。根据假设3，天牛头朝向任意，因而从天牛右须指向左须的向量的朝向也是任意的，所以可以产生一个随机向量dir=rands(n,1)来表示它。对此归一化：dir=dir/norm(dir)；我们这样可以得到xl-xr=d0dir；显然，xl，xr还可以表示成质心的表达式；xl=x+d0dir/2；xr=x-d0dir/2。
第二步：对于待优化函数f，求取左右两须的值：felft=f(xl)；fright=f(xr)；判断两个值大小，如果fleft<fright，为了探寻f的最小值，则天牛向着左须方向行进距离step，即x=x+stepnormal(xl-xr)；如果fleft>fright，为了探寻f的最小值，则天牛向着右须方向行进距离step，即x=x-stepnormal(xl-xr)；如以上两种情况可以采用符号函数sign统一写成：x=x-stepnormal(xl-xr)sign(fleft-fright)=x-stepdir*sign(fleft-fright)。
(注：其中normal是归一化函数)

循环迭代：
dir=rands(n,1)；dir=dir/norm(dir)；%须的方向
xl=x+d0dir/2；xr=x-d0dir/2；%须的坐标
felft=f(xl)；fright=f(xr)；%须的气味强度
x=x-stepdirsign(fleft-fright)。%下一步位置
关于步长:
两种推荐：
每步迭代中采用step=etastep，其中eta在0，1之间靠近1，通常可取eta=0.95；
引入新变量temp和最终分辨率step0，temp=etatemp，step=temp+step0.
关于初始步长：初始步长可以尽可能大，最好与自变量最大长度相当。

⛄二、ELMAN神经网络简介

1 Elman网络特点
Elman神经网络是一种典型的动态递归神经网络，它是在BP网络基本结构的基础上，在隐含层增加一个承接层，作为一步延时算子，达到记忆的目的，从而使系统具有适应时变特性的能力，增强了网络的全局稳定性，它比前馈型神经网络具有更强的计算能力，还可以用来解决快速寻优问题。
2 Elman网络结构
Elman神经网络是应用较为广泛的一种典型的反馈型神经网络模型。一般分为四层：输入层、隐层、承接层和输出层。其输入层、隐层和输出层的连接类似于前馈网络。输入层的单元仅起到信号传输作用，输出层单元起到加权作用。隐层单元有线性和非线性两类激励函数，通常激励函数取Signmoid非线性函数。而承接层则用来记忆隐层单元前一时刻的输出值，可以认为是一个有一步迟延的延时算子。隐层的输出通过承接层的延迟与存储，自联到隐层的输入，这种自联方式使其对历史数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到动态建模的目的。其结构图如下图1所示，
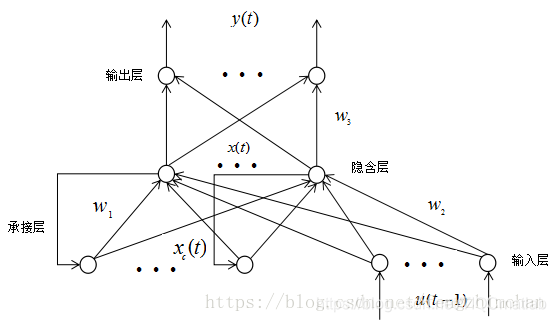
在这里插入图片描述
其网络的数学表达式为：

3 Elman网络与BP网络的区别
它是动态反馈型网络，它能够内部反馈、存储和利用过去时刻输出信息，既可以实现静态系统的建模，还能实现动态系统的映射并直接反应系统的动态特性，在计算能力及网络稳定性方面都比BP神经网络更胜一筹。
4 Elman网络缺点
与BP神经网络一样，算法都是采用基于梯度下降法，会出现训练速度慢和容易陷入局部极小点的缺点，对神经网络的训练较难达到全局最优。

⛄三、部分源代码

clear all
clc

%% bas优化elman网络

%% 自变量个数
x_number=49;
%% 因变量个数
y_number=1;
%% 网络节点个数
inputnum=x_number; % 输入层
hiddennum=50; % 隐含层
outputnum=y_number; % 输出层
iterations=2000; % 迭代次数

%% 导入数据
[data_train,~,raw_train]=xlsread(‘train.xlsx’);
[data_predict,~,raw_predict]=xlsread(‘predict.xlsx’);
%% 自变量
x_train=data_train(2:366,5:end);
x_test=data_train(367:397,5:end);
%% 因变量
y_train=data_train(367:731,6);
y_test=data_predict(2:end,6);
%% 自变量归一化
[x,xn]=mapminmax([x_train;x_test]‘,-1,1);
trainx=x(:,1:size(x_train,1));
testx=x(:,size(x_train,1)+1:end);
%% 因变量归一化
[trainy,yn]=mapminmax(y_train’,-1,1);

%% 维度
global dim
dim=inputnumhiddennum+hiddennumhiddennum+outputnumhiddennum+hiddennumoutputnum+outputnum;

%% 构建神经网络
net=newelm(trainx,trainy,hiddennum,{‘tansig’,‘purelin’},‘traingdm’); %% ELman网络训练

%% 天牛左右须距离
d0=0.5;
%% 系数
c=2;
%% 初始化步进长度
step=2;
%% 最大值
popmax=0.5;
%% 最小值
popmin=-0.5;
%% 步长更改系数
eta=0.995;
%% 自变量个数
nvars=dim;

%% 初始化
x=popmin+(popmax-popmin)*rand(1,nvars);

%% 记录每次迭代的最优个体
xbest=x;

%% 记录最优值
fbest=fun(xbest,inputnum,hiddennum,outputnum,net,trainx,trainy);
fbest_store=fbest; % 记录每次迭代的最优值
% figure(1)
% plot(1,fbest,‘k.’,‘linewidth’,2)
% hold on
% title([‘bas优化最优解：’,num2str(fbest)],‘fontsize’,30)
% pause(0.1)
function error = fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn)
%% 该函数用来计算适应度值

%% 提取个体
iw1=x(1:inputnumhiddennum);
lw1=x(inputnumhiddennum+1:inputnumhiddennum+hiddennumhiddennum);
lw2=x(inputnumhiddennum+hiddennumhiddennum+1:inputnumhiddennum+hiddennumhiddennum+outputnum*hiddennum);
b1=x(end-outputnum-hiddennum+1:end-outputnum);
b2=x(end-outputnum+1:end);

%% 网络权值赋值
net.iw{1,1}=reshape(iw1,hiddennum,inputnum);
net.lw{1,1}=reshape(lw1,hiddennum,hiddennum);
net.lw{2,1}=reshape(lw2,outputnum,hiddennum);
net.b{1}=b1’;
net.b{2}=b2’;

% %设置训练参数
% net.trainParam.show=100; %每100代显示
% net.trainParam.mem_reduc=1;
% net.trainParam.mc=0.8; %动量因子
% net.trainParam.Ir=0.9; % 学习率
% net.trainParam.epochs=500; %训练的代数
% net.trainParam.goal=0.00001; %目标误差
% net.trainParam.max_fail=100;

% % 训练向前向神经网络
% net=train(net,inputn,outputn);
%% 网络训练
an=sim(net,inputn);
%% 误差
error=mean(mean(abs(an-outputn)));
end