二叉树

1.树
- 1.1定义
- 1.2基本术语
- 1.3树形结构和线性结构
- 1.4树的存储结构
- - 1.4.1双亲表示法
  - 1.4.2孩子兄弟表示法
2.二叉树
- 2.1定义
- 2.2特殊二叉树
- 2.3性质
- 2.4存储结构
- - 2.4.1顺序存储
  - 2.4.2链式存储结构
3.二叉树的基本操作
- 3.1前序遍历（先序遍历）
- 3.2中序遍历
- 3.3后序遍历
- 3.4层序遍历
4.二叉树练习
5.二叉树的创建和销毁
- 5.1二叉树的创建
- 5.2二叉树的销毁

1.树

学习二叉树，首先得了解树，从树的基本概念出发。

1.1定义

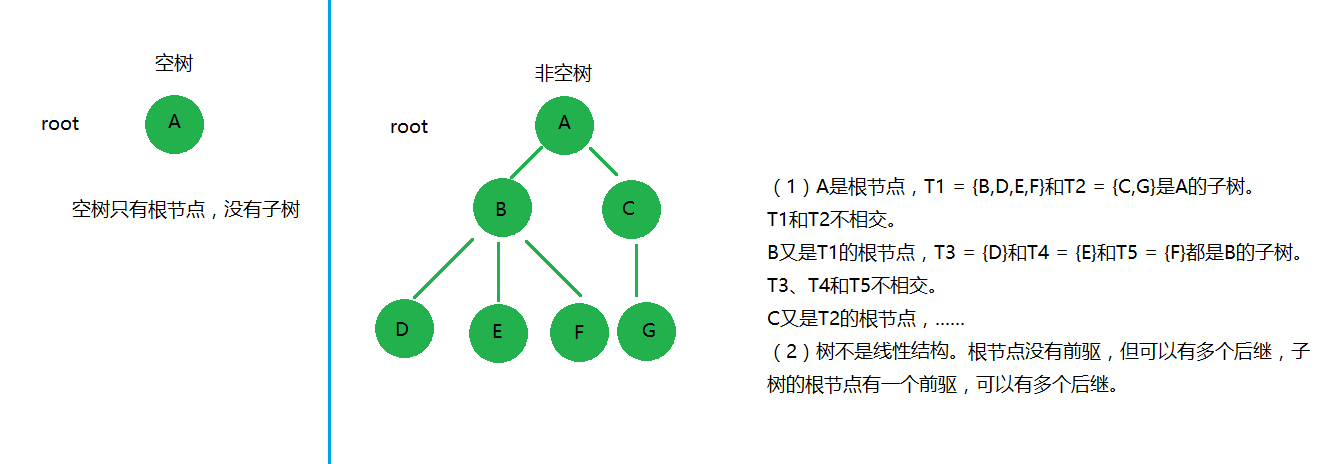
树是n个节点的的有限集合，是一种非线性结构。当n=0时称为空树，对于非空树T：（1）只有一个根结点（root）；（2）除根节点外的其余结点可分为m个互不相交的有限集T1，T2，……，Tm，其中每个集合本身又是一棵树，称为根的子树。
在这里插入图片描述

1.2基本术语

结点：树的一个独立单元，包含一个数据元素或者指向其子树的分支。如图中的A，B，C等。
结点的度：结点拥有的子树数称为结点的度（也可以理解为这个结点有多少个孩子）。如A的度是2，B的度是3，D的度是0。
树的度：树的各个结点的度的最大值。如图中的树的度为3。
叶子结点（或者终端结点）：度为0的结点。如图中的D，E，F，G。
非终端结点：度不为0的结点。除根结点外，非终端结点也称为内部结点。如图中B，C。
孩子结点（或者子节点）：一个结点的子树的根结点称为该结点的孩子结点。如图中B和C是A的子结点。
双亲结点（或者父结点）：一个结点有一个子结点，该结点称为其子结点的父结点。如图中，A是B和C的双亲结点。
兄弟结点：同一双亲的孩子之间互称兄弟。如图中B和C是兄弟结点。
祖先：从根结点到该结点所经分支上的所有结点。如D的祖先是A和B。
子孙：以某结点为根的子树的任一结点都称为该结点的子孙。如D，E，F是B的子孙。
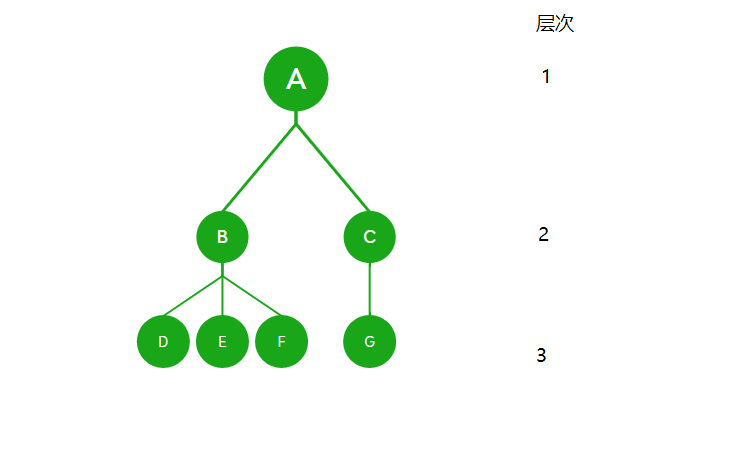
层次：从根结点开始，根结点为第一层，根的孩子为第二层，以此类推直到最后一层。如A是第一层，B是第二层，D是第三层。
深度：树中结点的最大层次。如A这棵树的深度是3。
森林：由m棵互不相交的树构成的集合。如去掉A结点，B和C这两棵子树就是森林。

这么多概念，但常用的只有结点的度、双亲结点、叶子结点、树的层次、树的高度、结点的祖先和子孙。

在这里插入图片描述

1.3树形结构和线性结构

树形结构	线性结构
树的根结点没有双亲结点	线性表的第一个元素没有前驱
树的叶子结点没有子结点	线性表的最后一个元素没有后继
树的内部结点有一个前驱和多个后继	线性表的其余元素只有一个前驱和一个后继

1.4树的存储结构

树有多种存储结构：双亲表示法、孩子链表表示法、孩子兄弟表示法等。由于今天的猪脚是二叉树，所以在这里简单介绍下双亲表示法和孩子兄弟表示法。

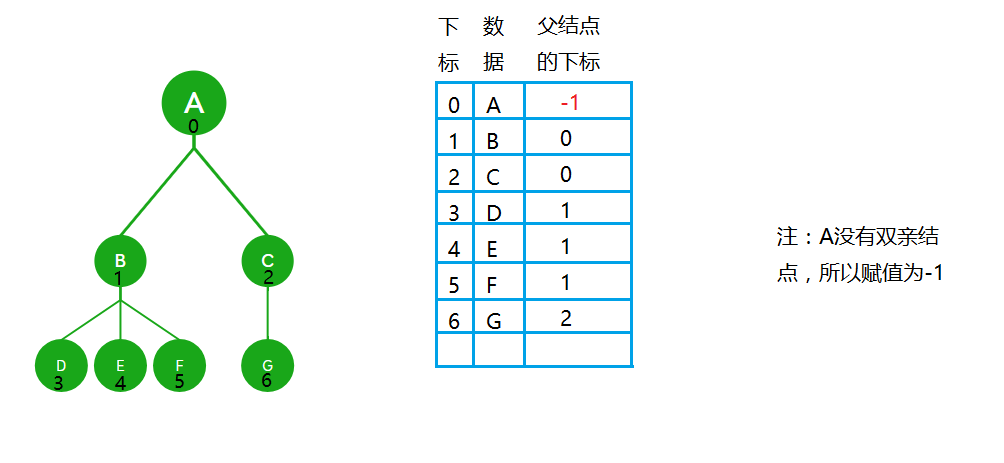
1.4.1双亲表示法

//结点
#define MAXSIZE 100
typedef int ElemType;
typedef struct
{ElemType x;//结点的数据int parent;//结点的双亲结点的下标
}PTNode;
typedef struct
{PTNode a[MAXSIZE];//结点数组int size;//结点个数
}PTree;

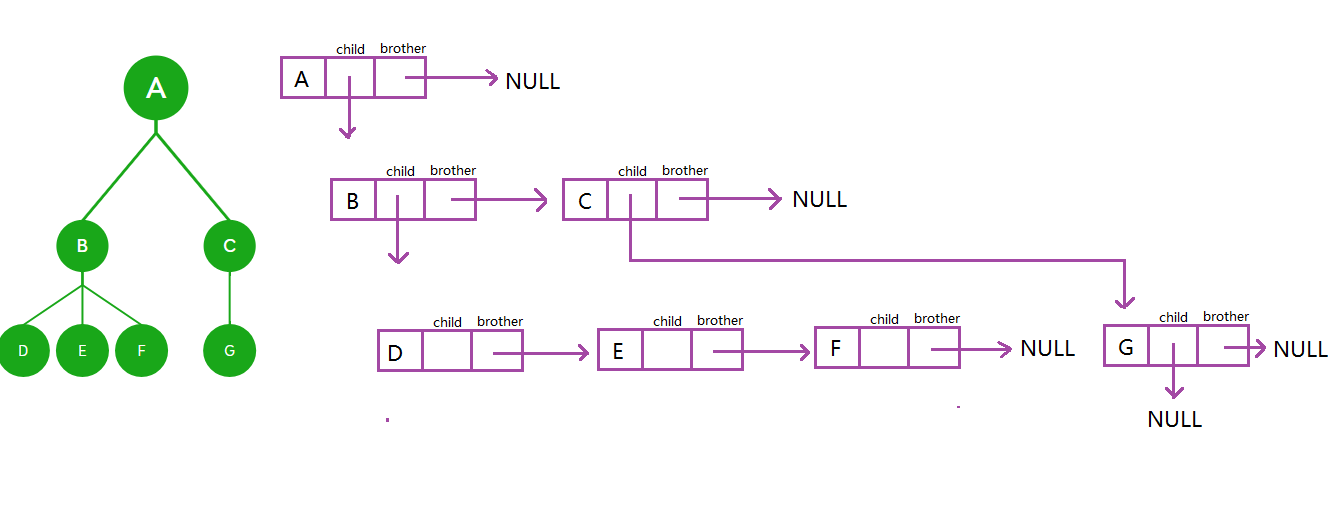
在这里插入图片描述

1.4.2孩子兄弟表示法

//结点
typedef int ElemType;
typedef struct CBTreeNode
{ElemType x;//数据struct CBTreeNode* firstchild;//指向结点的左孩子，也就是第一个孩子struct CBTreeNode* Nextbrother;//指向同一父结点的兄弟
}CBTNode;

在这里插入图片描述

2.二叉树

2.1定义

二叉树是n（n>=0）个结点的有限集合。当n=0时为空树，当n不为0时，二叉树有以下特点：1.每个结点的度不超过2（可以理解为二孩政策下的结点最多只能有两个孩子）；
2.每个结点的左子树和右子树顺序不能颠倒，所以二叉树是有序树。在这里插入图片描述

2.2特殊二叉树

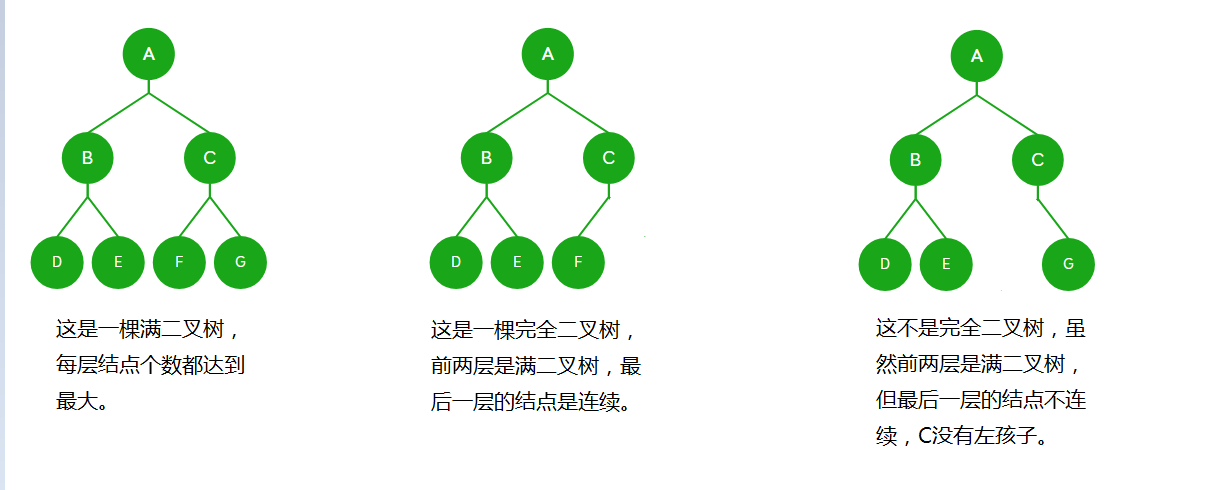
满二叉树：每一层结点数都达到最大，那么它就是满二叉树。如第1层最多有2 ^0个结点，第2层最多有 2 ^1个结点，则第k层最多有2 ^(k-1)个结点，假设这棵满二叉树有k层，那么它总共有2 ^0+2 ^1+……+2 ^(k-1) = 2 ^k-1个结点。
完全二叉树：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时，称为完全二叉树。（简介版：完全二叉树的前k-1层是满二叉树，最后一层从左到右依次连续）

在这里插入图片描述

2.3性质

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个结点。
若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h-1。
对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。
证明
若规定根节点的层数为1，具有n个结点的满二叉树的深度，h= log (n+1)(ps:log是以2
为底，n+1为对数)。
证明
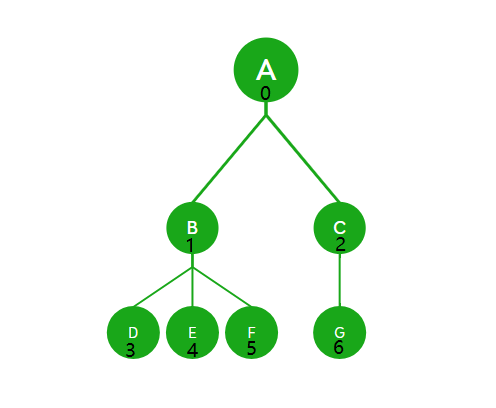
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
（1）. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
（2）. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
（3）.若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

2.4存储结构

2.4.1顺序存储

二叉树的顺序存储是用数组存储的，其中结点之间的关系用下标来表示。即二叉树的逻辑结构是树，但是其物理结构是数组。
在这里插入图片描述
但这种存储结构会造成空间浪费，适用于完全二叉树和满二叉树。

但这个结构却可以来实现一个很牛逼的排序：堆排序。

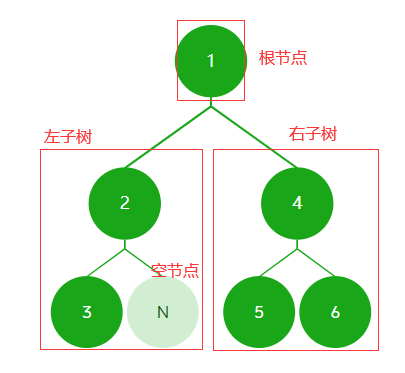
2.4.2链式存储结构

链式存储结构可以解决顺序存储结构浪费空间的问题，二叉树的链式存储表示有二叉链表、三叉链表、双亲链表、线索链表等。这里重点讲二叉链表。

//二叉树的节点
typedef int DataType;
typedef struct BinaryTreeNode
{DataType val;struct BinaryTreeNode* left;//指向左孩子的指针struct BinaryTreeNode* right;//指向右孩子的指针
}BTNode;

在这里插入图片描述

下面讲二叉树的基本操作。

3.二叉树的基本操作

遍历是指每个结点被访问一次且仅被访问一次。二叉树有一个前驱和两个后继，这注定其遍历不同于线性结构的遍历。二叉树的遍历有前序遍历、中序遍历，后序遍历，层序遍历。

3.1前序遍历（先序遍历）

概念
前序遍历：先访问根节点，再访问左子树和右子树。

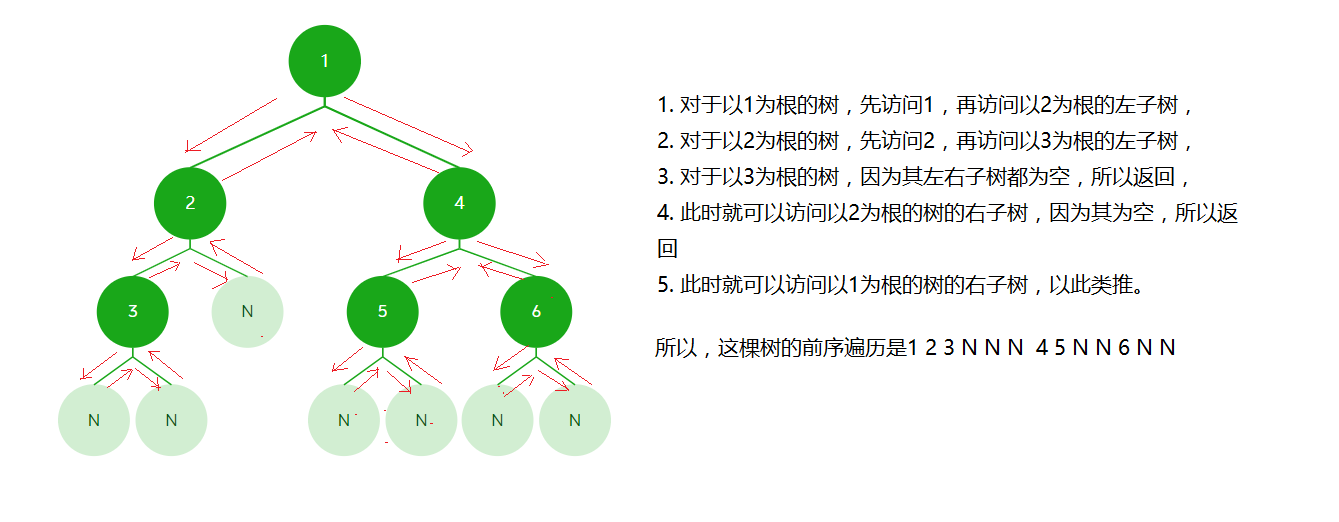
由图可知，树的前序遍历是递归的，所以可以用递归来实现。

代码实现

//先手动创建一个二叉树
BTNode* BuyNode(DataType x)//申请一个结点
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");return NULL;}newnode->left = newnode->right = NULL;newnode->val = x;return newnode;
}
BTNode* CreateBT()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;//返回根结点
}
//前序遍历
void PreOrder(BTNode* root)
{//思路：先访问根结点，再访问左子树和右子树if (root==NULL){printf("NULL ");return;}//先访问根结点printf("%d ", root->val);//再访问左右子树PreOrder(root->left);PreOrder(root->right);
}
int main()
{BTNode* root = CreateBT();PreOrder(root);return 0;
}

答案
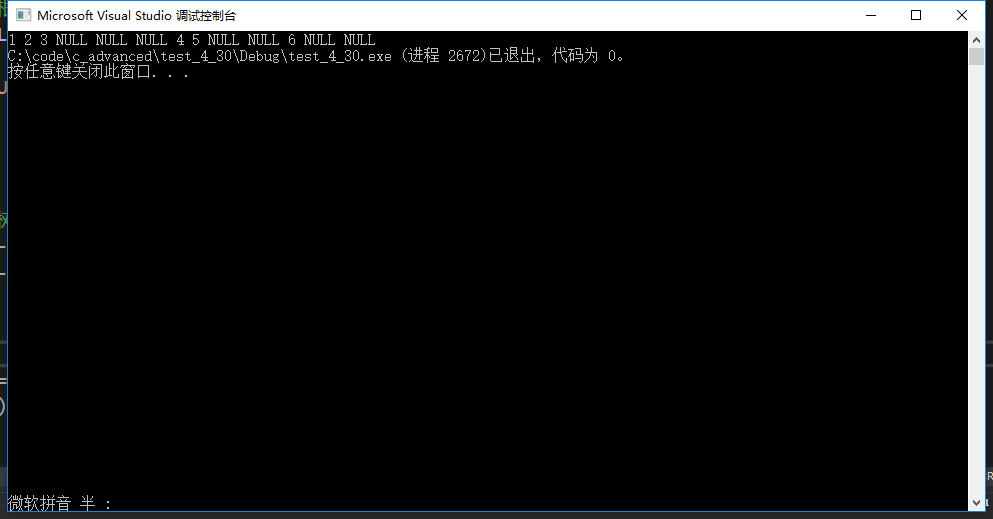
在这里插入图片描述

3.2中序遍历

概念
中序遍历：先访问左子树，再访问根节点，最后访问右子树。

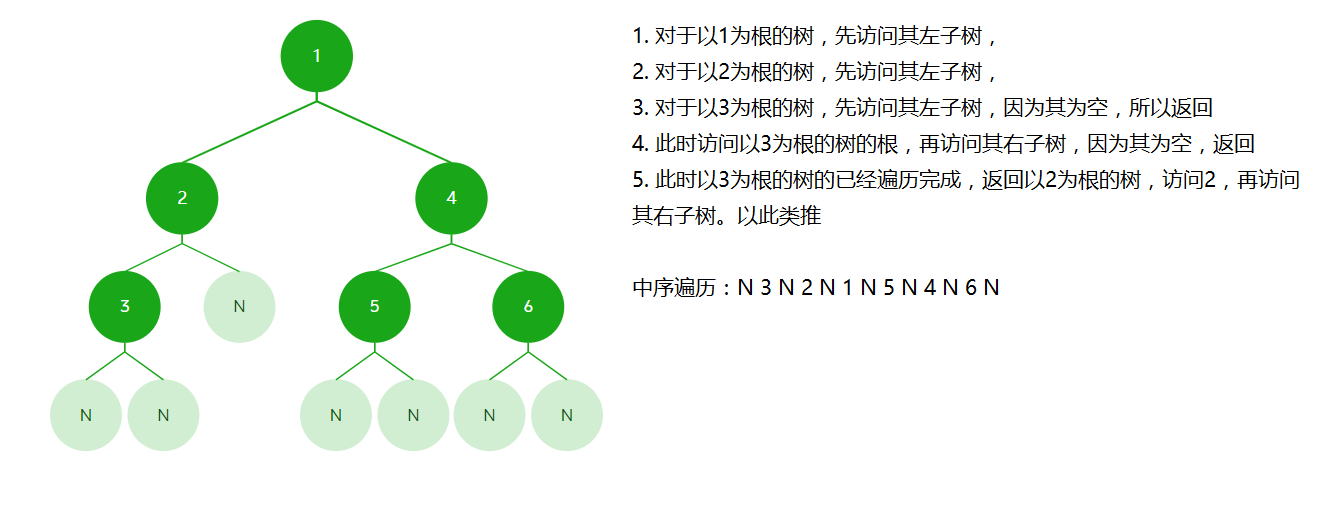
同样可以用递归实现
代码实现

// 二叉树中序遍历
void InOrder(BTNode* root)
{//思路：先访问左子树，再访问根节点，最后访问右子树if (root == NULL){printf("NULL ");return;}//先访问左子树InOrder(root->left);//再访问根节点printf("%d ", root->val);//最后访问右子树InOrder(root->right);
}

答案
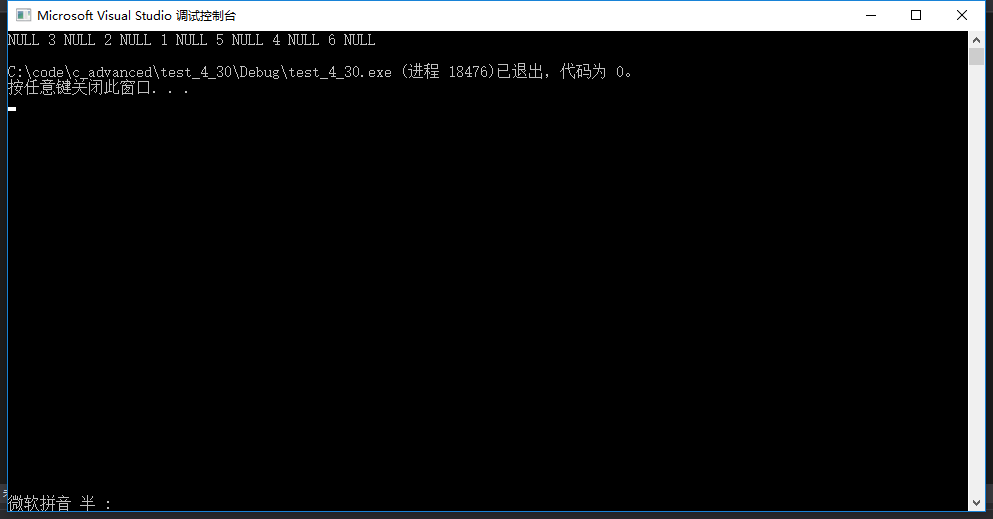
在这里插入图片描述

3.3后序遍历

概念
后序遍历：先访问左子树，再访问右子树，最后访问根节点。
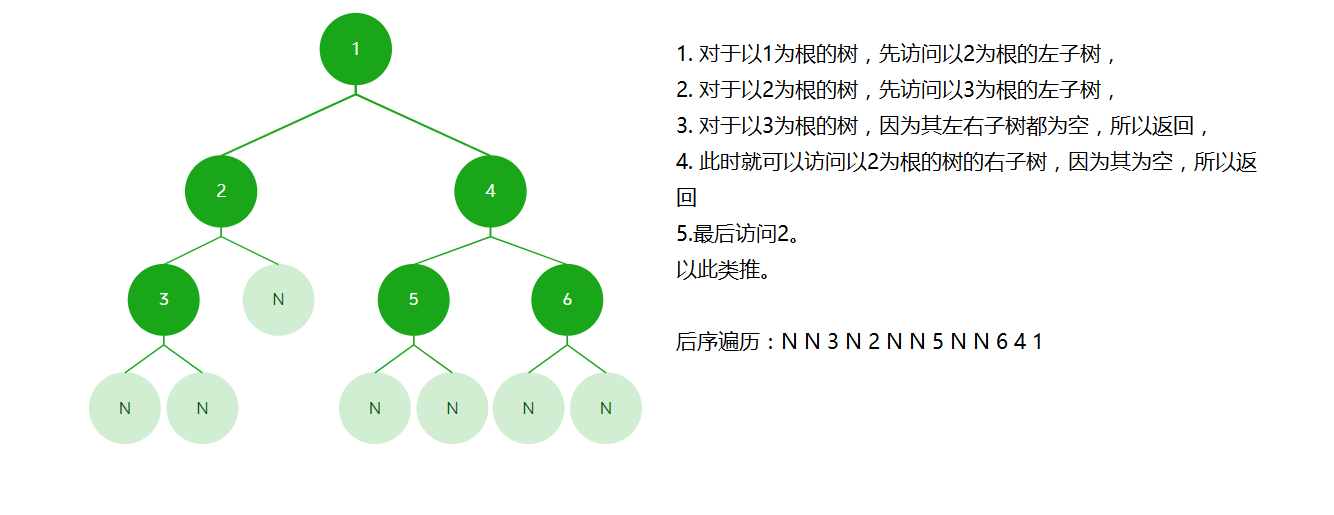
代码实现

//后序遍历
void PostOrder(BTNode* root)
{//思路：先访问左子树，再访问右子树，最后访问根结点if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}

答案
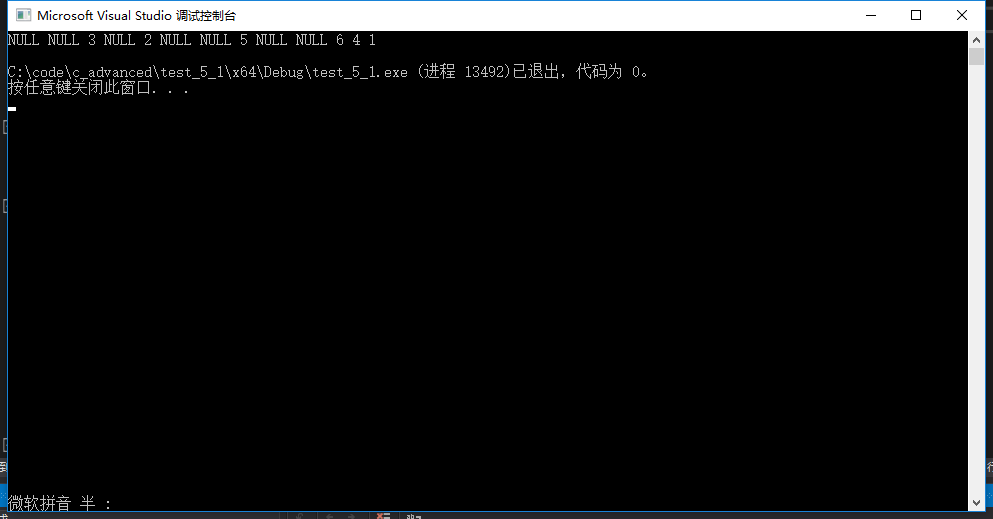
在这里插入图片描述

3.4层序遍历

概念
层序遍历：从上到下，从左到右，依次访问。
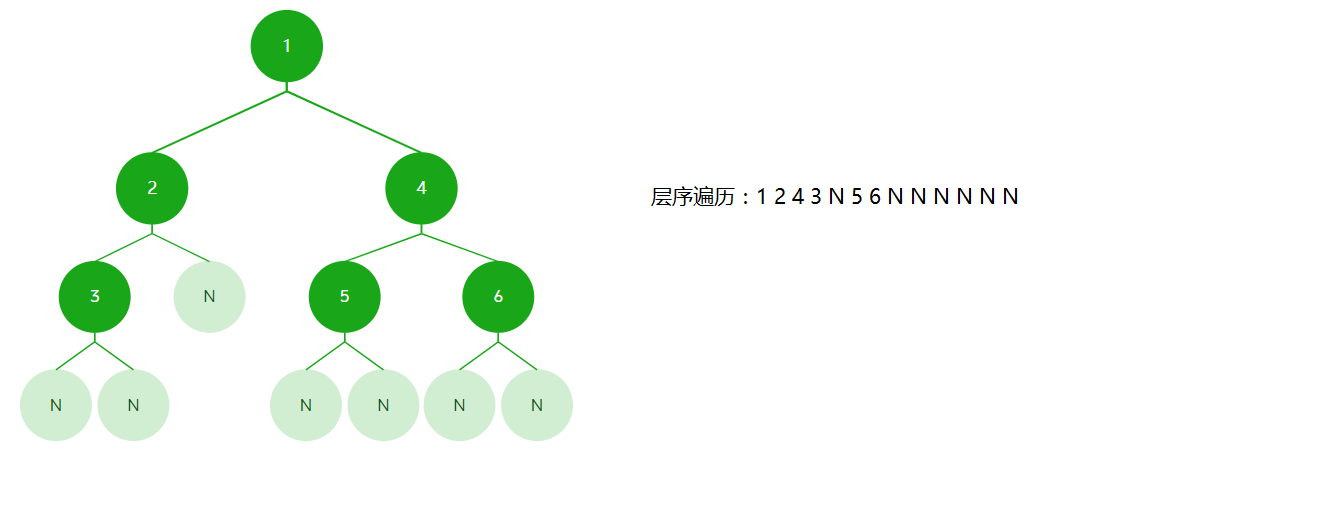
代码实现

// 层序遍历
void LevelOrder(BTNode* root)
{//思路：用队列实现，出队一层，入队下一层Queue q;QInit(&q);//如果非空就直接入队if (root){QPush(&q, root);}//队列中只入队非空元素while (!QEmpty(&q)){//先出队BTNode* tmp = QPop(&q);printf("%d ", tmp->val );//再判断左右子树是否为空if (tmp->left){QPush(&q, tmp->left);}if (tmp->right){QPush(&q, tmp->right);}}QDestroy(&q);
}

答案
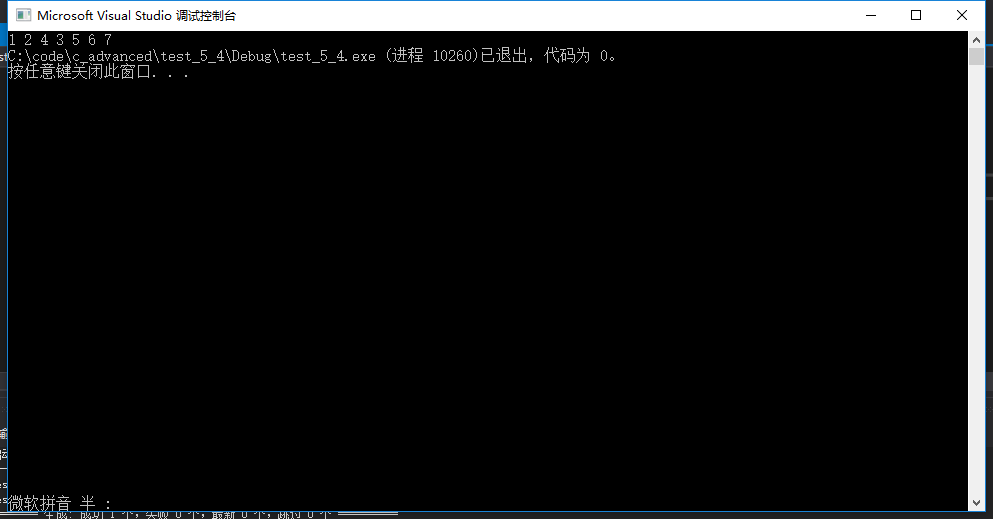
在这里插入图片描述

4.二叉树练习

样例
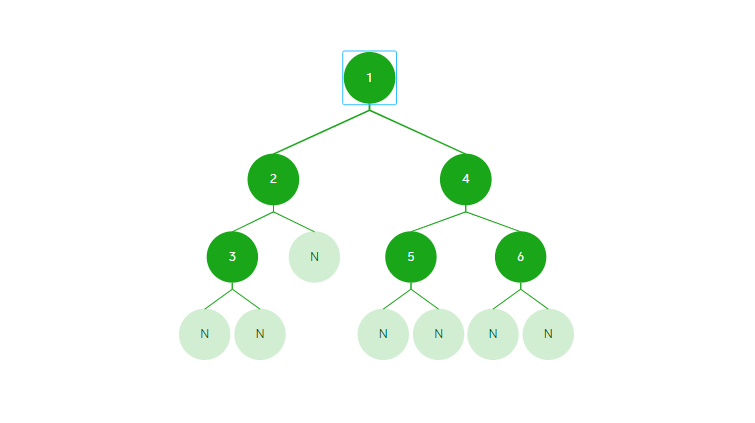
在这里插入图片描述

求二叉树的节点个数

// 二叉树节点个数//法一：
int size = 0;//也可以使用静态变量
void TreeSize(BTNode* root)
{//思路：只要节点不为空，就记录一次if (root == NULL){return 0;}++size;TreeSize(root->left);TreeSize(root->right);
}//法二：
int BinaryTreeSize(BTNode* root)
{//思路：二叉树的节点个数 = 左子树的节点个数 + 右子树的节点个数if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1 ;
}

注意
但是法一有个弊端：size是全局（或静态）变量，每次调用都得初始化一次。
答案
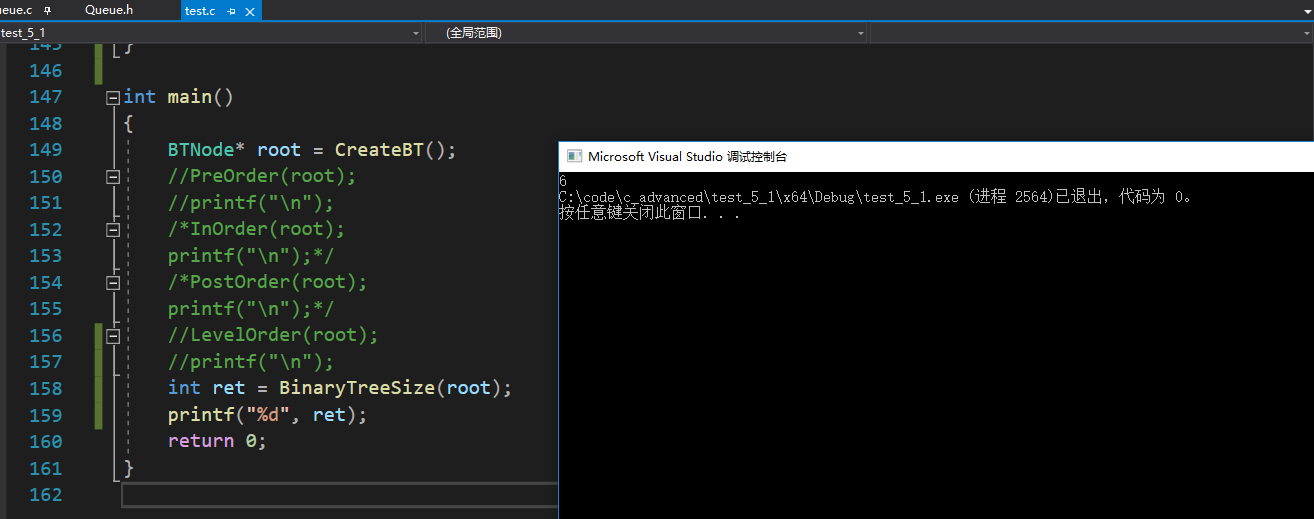
在这里插入图片描述

求二叉树的叶子节点个数

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{//思路：二叉树的叶子节点 = 左子树的叶子节点 + 右子树的叶子节点if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

答案
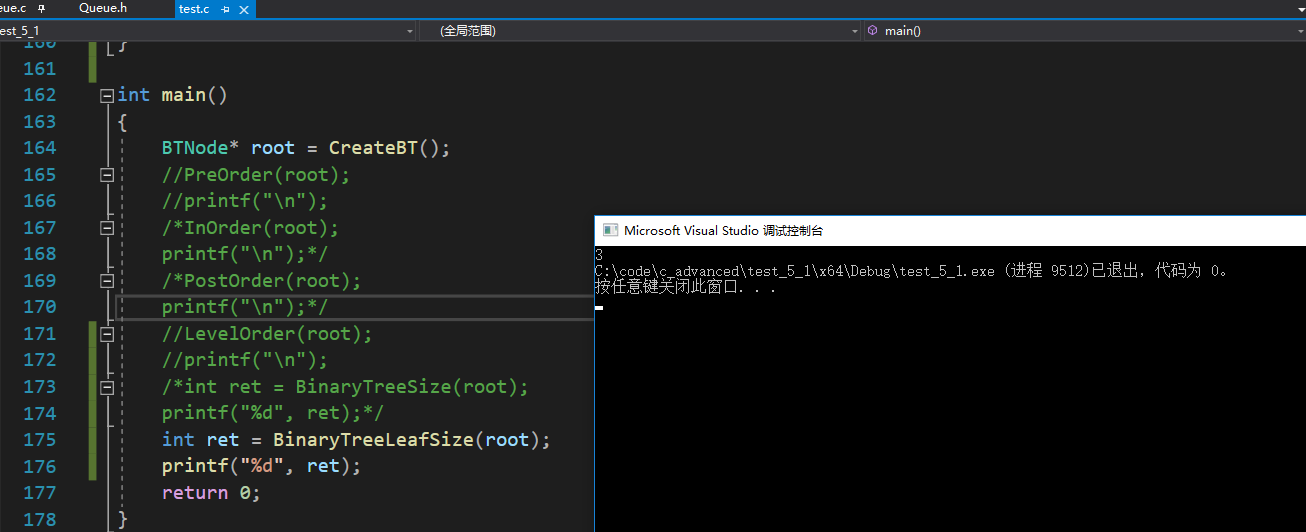
在这里插入图片描述

求二叉树的高度

// 二叉树的高度(深度)
int TreeHeight(BTNode* root)
{// 思路：二叉树的高度 = 左子树的高度和右子树的高度的最大值 + 1if (root == NULL){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return left > right ? left + 1 : right + 1;
}

答案
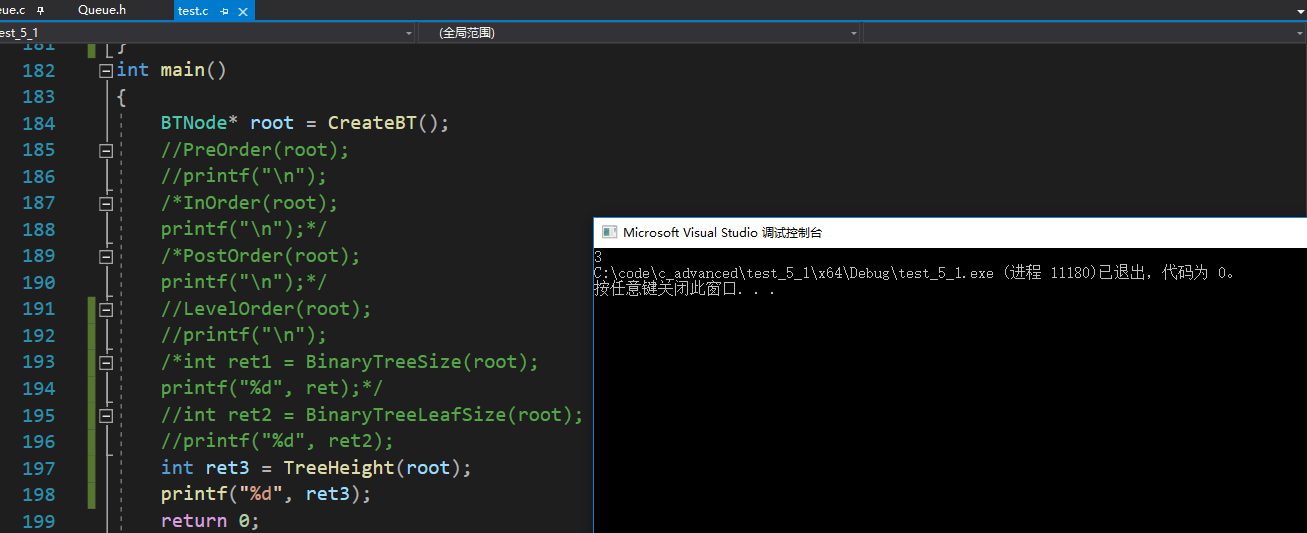
在这里插入图片描述

求第k层节点个数

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{//思路：//对于第一层，是求第k层节点个数（k）//对于第二层，是求第k-1层节点个数（k-1）//……//对于第k层，是求这一层节点个数（1）//第k层节点个数 = 左子树第k层节点个数 + 右子树第k层节点个数if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

答案
在这里插入图片描述

判断是否是单值二叉树（LeetCode965）OJ链接
单值二叉树：二叉树的每个节点都有相同的值

// 判断是否是单值二叉树
bool isUnivalTree(BTNode* root)
{//思路：比较根节点与左右子树是否相等，不相等就返回false，相等就判断左右子树是否是单值二叉树if (root == NULL){return true;}if (root->left && root->left->val != root->val){return false;}if (root->right && root->right->val != root->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}

答案
在这里插入图片描述

查找一个值为x的节点

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, DataType x)
{//思路：先判断根的值是否与x相等，相等就返回根，//不等就判断是否与左子树相等，相等就返回//不等就判断是否与右子树相等，相等就返回，不等就返回NULLif (root == NULL){return NULL;}if (root->val == x){return root;}BTNode*tmp = BinaryTreeFind(root->left, x);if (tmp != NULL){return tmp;}tmp = BinaryTreeFind(root->right, x);if (tmp != NULL){return tmp;}return NULL;
}

判断两棵二叉树是否相等（LeetCode100）OJ链接

// 判断两棵二叉树是否相等
bool isSameTree(BTNode* p, BTNode* q)
{//思路：先判断根结点是否相等，再判断左子树是否相等，最后判断右子树是否相等if (p == NULL && q == NULL){return true;}if (p == NULL || q == NULL){return false;}if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

答案
在这里插入图片描述

判断是否是对称二叉树（LeetCode101）OJ链接

bool isLefRig(BTNode* p1, BTNode* p2)//功能类似于判断两棵二叉树是否相等
{if (p1 == NULL && p2 == NULL){return true;}if (p1 == NULL || p2 == NULL){return false;}if (p1->val != p2->val){return false;}return isLefRig(p1->left, p2->right) && isLefRig(p1->right, p2->left);
}
bool isSymmetric(BTNode* root)
{
·	//思路：写一个辅助函数，功能与判断二叉树是否相等类似if (root == NULL){return true;}return isLefRig(root->left, root->right);
}

答案
在这里插入图片描述

二叉树的前序遍历（LeetCode144）OJ链接

int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void PreOrder(struct TreeNode* root, int* a, int* i)
{if (root == NULL){return;}//先对根结点进行操作，再对左右子树进行操作a[(*i)++] = root->val;PreOrder(root->left, a, i);PreOrder(root->right, a, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){//我们需要知道这棵树的大小，再来动态申请int size = TreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//写一个函数来实现遍历，不要在这个函数遍历，因为遍历需要递归，所以TreeSize会重复调用int i = 0;//用来记录数组的下标，方便存储数据PreOrder(root, ret, &i);//为什么要传下标的地址？因为要对下标进行修改return ret;
}

答案
在这里插入图片描述

二叉树的中序遍历（LeetCode94）OJ链接

int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
void InOrder(struct TreeNode* root, int* a, int* i)
{if (root == NULL){return;}InOrder(root->left, a, i);a[(*i)++] = root->val;InOrder(root->right, a, i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){//我们需要知道这棵树的大小，再来动态申请int size = TreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//写一个函数来实现遍历，不要在这个函数遍历，因为遍历需要递归，所以TreeSize会重复调用int i = 0;//用来记录数组的下标，方便存储数据InOrder(root, ret, &i);//为什么要传下标的地址？因为要对下标进行修改return ret;
}

结果
在这里插入图片描述

二叉树的后序遍历（LeetCode145）OJ链接

int BinaryTreeSize(struct TreeNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
void PostOrder(struct TreeNode* root, int* ret, int* pi)
{if (root == NULL){return 0;}PostOrder(root->left, ret, pi);PostOrder(root->right, ret, pi);ret[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){int size = BinaryTreeSize(root);*returnSize = size;int* ret = (int*)malloc(sizeof(int) * size);//用来存放前序序列int i = 0;PostOrder(root, ret, &i);return ret;
}

结果
在这里插入图片描述

判断一棵树是否是另一棵树的子树

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{//思路：用当前节点所在树与sub进行比较，相等返回真，不相等用当前根结点的左子树比较，再不相等用右子树比较if (root == NULL){return false;}if (isSameTree(root, subRoot)){return true;}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

结果
在这里插入图片描述

判断是否是完全二叉树

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{//思路：利用层序遍历，将完全二叉树的所有节点全部入队，//当出队时节点为NULL，如果为完全二叉树，则队列中的其余节点都是NULL，//所以最后判断队列中的节点是否不为NULL，即可判断Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode*tmp = QueueFront(&q);QueuePop(&q);if (tmp == NULL){break;//当遇到NULL，就跳出循环}else{QueuePush(&q, tmp->left);//如果为NULL也入队QueuePush(&q, tmp->right);}}while (!QueueEmpty(&q)){BTNode* tmp = QueueFront(&q);QueuePop(&q);if (tmp){QueueDestroy(&q);//注意销毁队列，防止内存泄漏return false;}}QueueDestroy(&q);//等下学习怎么销毁，先记住它有销毁的功能return true;
}
int main()
{char arr[100] = { 0 };scanf("%s", arr);int i = 0;int size = strlen(arr);BTNode* root = CreateBT(arr, &i,size);InOrder(root);
}

5.二叉树的创建和销毁

前面的二叉树是我们手动创建的，现在学习了前序、中序、后序遍历，就可以利用它们来创建和销毁二叉树。

5.1二叉树的创建

二叉树遍历OJ链接

BTNode* BuyNode(DataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc failed");return NULL;}newnode->left = NULL;newnode->right = NULL;newnode->val = x;return newnode;
}
BTNode* CreateBT(char* arr, int* pi,int size)
{	//ABC##DE#G##F###if (*pi == size)//递归的停止条件{return NULL;}if (arr[*pi] == '#'){(*pi)++;//遇到#,不要忘记跳过return NULL;}BTNode* root = BuyNode(arr[(*pi)++]);root->left = CreateBT(arr, pi,size);root->right = CreateBT(arr, pi,size);return root;
}
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
}
int main()
{char arr[100] = { 0 };scanf("%s", arr);int i = 0;int size = strlen(arr);BTNode* root = CreateBT(arr, &i,size);InOrder(root);
}

结果
在这里插入图片描述

5.2二叉树的销毁

// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{//如果用前序或者中序遍历销毁二叉树会导致内存泄漏（找不到左右子树）//所以用后序遍历销毁二叉树if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);root == NULL;
}