第k个数

给定一个长度为 nn 的整数数列 a1,a2,…,ana1,a2,…,an，以及一个整数 kk。

请你计算并输出该数列从大到小排序后的第 kk 个数。

输入格式

第一行包含两个整数 n,kn,k。

第二行包含 nn 个整数 a1,a2,…,ana1,a2,…,an。

输出格式

一个整数，表示数列从大到小排序后的第 kk 个数。

数据范围

前三个测试点满足 1≤n≤101≤n≤10。
所有测试点满足 1≤n≤10001≤n≤1000，1≤k≤n1≤k≤n，0≤ai≤1000≤ai≤100。

输入样例1：

5 3
20 10 30 40 10

输出样例1：

输入样例2：

6 5
90 20 35 40 60 100

输出样例2：

输入样例3：

4 3
4 3 3 2

输出样例3：

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++) 
using namespace std;
typedef long long LL; 
int a[1001];
bool cmp(int a,int b)
{return a>b;
}
int main()
{int n,k;cin>>n>>k;rep(i,1,n)cin>>a[i];sort(a+1,a+1+n,cmp);cout<<a[k];
}

多米诺骨牌

将 nn 块多米诺骨牌排成一排，每块骨牌垂直竖立。

开始时，同时将一些骨牌推倒，有的向右倒，有的向左倒。

保证这些开始就被推倒的骨牌中，任意两块倒向同一方向的骨牌之间都至少存在一块倒向反方向的骨牌。

每一秒后，每个向左倒的骨牌都会推倒其左侧相邻的骨牌，每个向右倒的骨牌都会推倒其右侧相邻的骨牌。

如果在某一时刻，某骨牌两侧的相邻骨牌同时倒向它，则由于力的平衡，该骨牌会保持垂直竖立不变。

下图给出了此过程的一个可能示例。

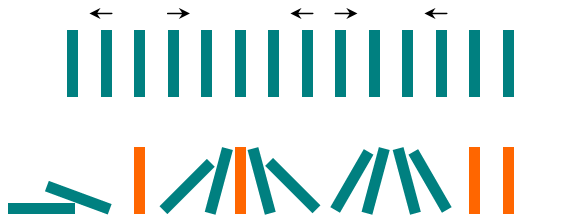
给定每块骨牌的初始状态，请你判断在推倒过程完全结束后，有多少块骨牌仍然保持垂直竖立。

输入格式

第一行包含整数 nn。

第二行包含一个长度为 nn 的字符串，其中的第 ii 个字符表示第 ii 个骨牌的初始状态：

L 表示该骨牌开始时向左倒。
R 表示该骨牌开始时向右倒。
. 表示该骨牌开始时不倒。

保证，对于 (i,j)(i,j)：

如果 i<ji<j 且 sisi 和 sjsj 均为 L，则一定存在 kk 满足 i<k<ji<k<j 且 sksk 为 R。
如果 i<ji<j 且 sisi 和 sjsj 均为 R，则一定存在 kk 满足 i<k<ji<k<j 且 sksk 为 L。

输出格式

一个整数，表示最终保持垂直竖立的骨牌数量。

数据范围

前 66 个测试点满足 1≤n≤151≤n≤15。
所有测试点满足 1≤n≤30001≤n≤3000。

输入样例1：

14
.L.R...LR..L..

输出样例1：

输入样例2：

5
R....

输出样例2：

输入样例3：

1
.

输出样例3：

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 3010;int n;
string s;
int l[N], r[N];
int main () 
{cin >> n >> s;s = ' ' + s;for (int i = 1; i <= n; i ++ ) if (s[i] == 'R') l[i] = i;else if (s[i] != 'L') l[i] = l[i - 1];for (int i = n; i >= 1; i -- ) if (s[i] == 'L') r[i] = i;else if (s[i] != 'R') r[i] = r[i + 1];int ans = 0;for (int i = 1; i <= n; i ++ )if (((!l[i] && !r[i]) || (l[i] && r[i] && i - l[i] == r[i] - i)) && s[i] == '.') ans ++ ;cout << ans;return 0;
}

构造序列

请你构造一个 0101 序列，序列需要满足以下所有要求：

恰好包含 nn 个 00 和 mm 个 11。
不存在两个或两个以上的 00 连续相邻。
不存在三个或三个以上的 11 连续相邻。

输入格式

共一行，包含两个整数 n,mn,m。

输出格式

输出共一行，如果存在满足条件的 0101 序列，则输出满足条件的 0101 序列，否则输出 -1。

如果答案不唯一，则输出任意合理答案均可。

数据范围

前 66 个测试点满足 1≤n,m≤101≤n,m≤10。
所有测试点满足 1≤n,m≤1061≤n,m≤106。

输入样例1：

1 2

输出样例1：

输入样例2：

4 8

输出样例2：

110110110101

输入样例3：

4 10

输出样例3：

11011011011011

输入样例4：

1 5

输出样例4：

-1

#include <bits/stdc++.h>
using namespace std;int main()
{int n, m;scanf("%d%d", &n, &m);if (m >= n - 1 && m <= 2 * n + 2){m -= n - 1;if (m == 1) {printf("10"); m = 0;}else if (m >= 2) {printf("110"); m -= 2;}else printf("0");for (int i = 2; i <= n; i ++ ){if (m >= 1) {printf("110"); m -- ;}else printf("10");}if (m == 2) printf("11");if (m == 1) printf("1");}else puts("-1");return 0;
}