前言
解释器模式是一种使用较少的行为型模式;
提供了一种解释语言的语法或表达式的方式,通过该接口解释一个特定的上下文。
定义:给定一个语言,定义它的文法的一种表示,并定义一个解释器,该解释器使用该表示来解释语言中的句子。
使用场景:
-
如果某个简单的语言需要解释执行而且可以将该语言中的语句表示为一个抽象语法树时,可以考虑使用解释器模式。
如一个简单的含有加减运算的数学表达式:p+q+m-n,像这样的表达式其构成无非就两种,一种是以pqmn这类的具体参数表示的符号,其无法再被推导,我们称为终结符号;另一种则是以“+”和“-”构成的算术运算符,在该运算法的两边总能找到有意义的具体计算参数,我们称其为非终结符号; -
在某些特定的领域出现不断重复的问题时,可以将该领域的问题转化为一种语法规则下的语句,然后构建解释器来解释该语句;
UML类图:
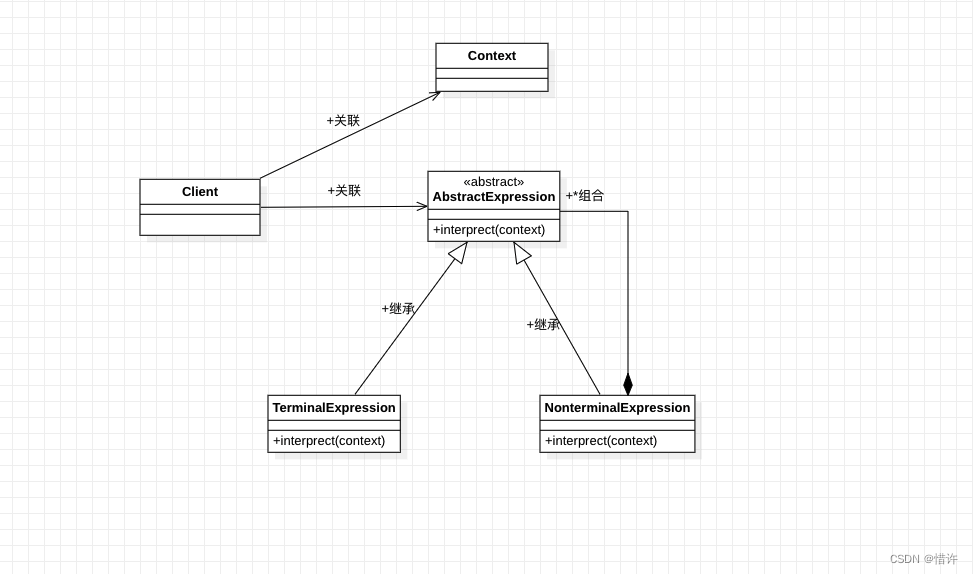
AbstractExpression:抽象表达式;
声明一个抽象的解释操作父类,并定义一个抽象的解释方法,其具体的实现在各个具体的子类解释器中完成;TerminalExpression:终结符表达式;
实现文法中与终结符有关的解释操作。文法中每一个终结符都有一个具体的终结表达式与之对应。NonterminalExpression:非终结符表达式;
实现文法中与非终结符有关的解释操作;Context:上下文环境类;
包含解释器之外的全局信息;Client:客户类;
解析表达式,构建抽象语法树,执行具体的解释操作等;
实现示例
这里我们以对算法表达式的解释举例,如表达式m+n+p,我们使用解释器对该表达式进行解释,那么代表数字的m、n、p三个字母可以看成终结符号,而+这个算术运算符号可以当做非终结符号。
- 定义抽象解释器表示数学运算,
ArithmeticExpression
/*** 抽象表达式*/
abstract class ArithmeticExpression {/*** 抽象的解析方法* @return 解析得到具体的值*/abstract fun interpret(): Int
}
- 定义数字解析器,
NumExpression
/*** 数字解析器*/
class NumExpression(private val num: Int) : ArithmeticExpression() {override fun interpret(): Int {return num //直接返回对应数字}
}
- 定义运算符号抽象解释器,
OperatorExpression
/*** 运算符号抽象解释器 为所有运算符号解释器共性的提取* @param exp1 exp2 声明两个成员变量存储运算符号两边的数字解释器*/
abstract class OperatorExpression(private val exp1: ArithmeticExpression,private val exp2: ArithmeticExpression
) : ArithmeticExpression() {
}
- 定义加法运算抽象解释器,
AdditionExpression
/*** 加法运算抽象解释器*/
class AdditionExpression(private val exp1: ArithmeticExpression,private val exp2: ArithmeticExpression
) : OperatorExpression(exp1, exp2) {override fun interpret(): Int {return exp1.interpret() + exp2.interpret()}
}
- 测试类,进行验证;
object Test {@JvmStaticfun main(args: Array<String>) {println("计算结果为:" + calculator("1 + 2 + 3 + 5"))}/*** 用于存储并操作所有相关的解释器*/private val stackExpression = Stack<ArithmeticExpression>()private fun calculator(expression: String): Int {var exp1: ArithmeticExpressionvar exp2: ArithmeticExpression//假设这里表达式字符以空格进行分割val splits: List<String> = expression.split(" ")for (i in splits.indices) {if (splits[i] == "+") {//当前是+号,则将栈中的解释器取出来作为运算符号左边的解释器exp1 = stackExpression.pop()//下一个坐标数据作为运算符号右边的解释器exp2 = NumExpression(splits[i + 1].toInt())//构造加法运算解释器存放到栈中stackExpression.push(AdditionExpression(exp1, exp2))} else {if (i > 0 && splits[i - 1] == "+") {//上面+号后面的数据已经存放到AdditionExpression中continue}stackExpression.push(NumExpression(splits[i].toInt()))}}return stackExpression.pop().interpret()}
}
当我们想定义减法操作时,只需要继承OperatorExpression类进行扩展即可;
Android源码中的解释器模式
- 解析
AndroidManifest.xml的PackageParser类;
总结
优点:
灵活的扩展性,当我们想对文法规则进行扩展延伸时,只需要增加对应的非终结符解释器,并在构建抽象语法树时,使用到新增的解释器对象进行具体的解释即可;
缺点:
对于每一条文法都需要对应至少一个解释器,会生成大量的类,不利于后期维护,因此,对于过于复杂的文法不推荐使用解释器模式;
结语
如果以上文章对您有一点点帮助,希望您不要吝啬的点个赞加个关注,您每一次小小的举动都是我坚持写作的不懈动力!ღ( ´・ᴗ・` )