说明
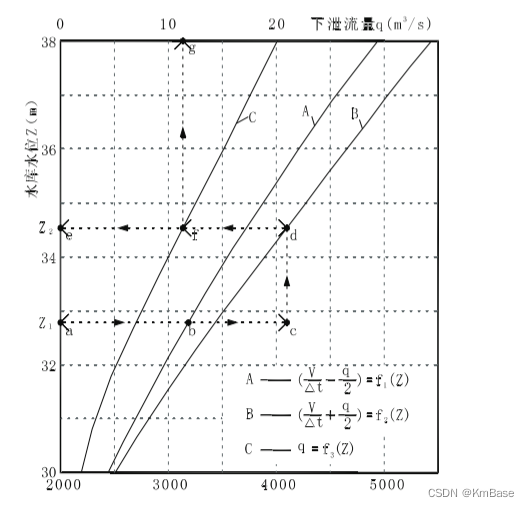
半图解法计算步骤如下:
(1)根据水位~库容关系、水位~泄流关系以及计算时段等绘制辅助曲线;
(2)确定起调水位 Z 1 Z_1 Z1及相应的 q 1 q_1 q1、 V 1 V_1 V1计算各时段平均入库流量 Q p Q_p Qp;
(3)在水位坐标轴上确定Z位置,记为a点。作水平线ac 交A线于b点,使 b c = Q p bc=Q_p bc=Qp。因A 线为 ( V / Δ t − q / 2 ) = f 1 ( Z ) (V/\Delta t-q/2)=f_1(Z) (V/Δt−q/2)=f1(Z),则 a b ab ab等于 ( V / Δ t − q / 2 ) (V/\Delta t-q/2) (V/Δt−q/2), a c ac ac等于 Q , + ( V Δ t − q / 2 ) = ( V / Δ t + q / 2 ) Q,+(V \Delta t- q /2)=(V/\Delta t+q/2) Q,+(VΔt−q/2)=(V/Δt+q/2)。
(4)在c点做垂线交B线于d点,由d点作水平线de 交Z坐标轴于e点,可见 d e = a c = ( V / Δ t + q / 2 ) de =ac=(V/\Delta t+q/2) de=ac=(V/Δt+q/2)。因B线为 ( V / A t + q / 2 ) = f ( Z ) (V/At+q/2)=f(Z) (V/At+q/2)=f(Z), d d d 点位于 B B B线上,则 e e e点为 Z Z Z值。
(5)过 d e de de与 C C C线交点f作垂线交 q q q坐标轴于 g g g点,则 g g g点为 q q q值。
(6)根据水量平衡得到下一时刻的 V V V。
(7)将 e e e点的 Z Z Z值作为第二时段的 Z Z Z,重复(2)~(6)即可得下一时段的特征值。由此逐时段进行计算,即可完成全部计算。
Python代码
def half_figure():z, v, q = util.ZVQ[:, 0], util.ZVQ[:, 1], util.ZVQ[:, 2]y = v*10**8/util.DT+q/2# 散点图plt.scatter(y, q, label='scatter')# 插值fyq = interpolate.interp1d(y, q, 'quadratic')ynew = np.linspace(min(y), max(y), len(y)*100)qnew = fyq(ynew)plt.plot(ynew, qnew, 'g--', label='interpolate')# 拟合z1 = np.polyfit(y, q, 3)p1 = np.poly1d(z1)plt.plot(y, p1(y), 'r-', label='polyfit')# 调整图像plt.xlabel("$\\frac{V}{\\Delta t}+\\frac{q}{2}(m^3/s)$")plt.ylabel("$q(m^3/s)$")plt.title("$q-\\frac{V}{\\Delta t}+\\frac{q}{2}$")plt.legend()plt.grid()plt.show()# 计算,采用拟合图像q_rk = util.QINT = q_rk.size(q_qs, q_ck, V, Z) = (0, # 起始流量np.zeros(T + 1), # 出库流量np.zeros(T + 1), # 水库蓄水过程np.zeros(T + 1)) # 水位过程Z[0] = util.Z_fxV[0] = util.fzv(Z[0])for t in range(0, T - 1):# print("<DEBUG> time [{}]".format(t))Q_T = util.fzq(Z[t]) # 最大过流能力q_ck[t] = q_qs + Q_T # 出库流量过程y2 = np.average([q_rk[t], q_rk[t+1]]) - q_ck[t] + V[t] / util.DT + q_ck[t] / 2 # 计算右侧q2 = p1(y2) # 查q2q_ck[t+1] = q2 # 放进结果V[t+1] = V[t] + ((q_rk[t] + q_rk[t+1]) * util.DT / 2 - (q_ck[t] + q_ck[t+1]) * util.DT / 2)/10**8 # 水量平衡Z[t+1] = util.fvz(V[t+1]) # 水位变化print(V[t])# 画水位变化plt.plot(Z[:-1])plt.title("$Z$")plt.xlabel("$T$")plt.ylabel("$Z(m)$")zmax = (np.where(Z == np.max(Z))[0][0], np.max(Z).round(1))plt.annotate("max{}".format(zmax), xy=zmax)plt.xlim(0)plt.grid()plt.show()# 画库容变化# plt.plot(V[:-1])# plt.title("$V$")# plt.xlabel("$T$")# plt.ylabel("$V(10^8m^3)$")# plt.grid()# plt.show()# 画入流出流过程线plt.plot(q_rk, '.-', label='In')inmax = (np.where(q_rk == np.max(q_rk))[0][0], np.max(q_rk))plt.plot(q_ck[:-2], 'r--', label='Out')omax = (np.where(q_ck == np.max(q_ck))[0][0], np.max(q_ck).round(1))plt.title("$In\\quad and\\quad Out(half-figure)$")plt.xlabel("$T(\\Delta T=1h)$")plt.ylabel("$Q(m^3/s)$")plt.annotate("max{}".format(inmax), xy=inmax)plt.annotate("max{}".format(omax), xy=omax)plt.xlim(0)plt.legend()plt.grid()plt.show()