路遥知马力——Momentum动量梯度

NAG:在滑板下降过程中也就是速度加快的时候增大水平方向的力(累计的动量方向) 而在上升的过程中也就是速度下降的时候
减少垂直方向的力（当前的梯度方向）两种情况下的最终结果
都是加大了往最优点方向的值加速了接近最优点的速度

本文收录在无痛的机器学习第一季。

写在前面：感谢

对本文的审阅和提出的宝贵意见，欢迎各位大神多多指点。

上一回扯了些关于梯度下降的事情，当然那只是个开头，有关梯度下降相关的内容非常多。为了保证完整性，今天再扯一下另外一个在梯度下降中十分重要的东西，那就是动量——momentum。

这是一个十分神秘的变量，我也只能以最简单的方式理解它，于是在这里班门弄斧了。正如它的中文名字一样，在优化求解的过程中，动量扮演了对之前优化量的持续发威的推动剂。一个已经完成的梯度+步长的组合不会立刻消失，只是会以一定的形式衰减，剩下的能量将继续发挥余热。我们先不加解释的给出基于动量的梯度下降的代码：

def momentum(x_start, step, g, discount = 0.7):   x = np.array(x_start, dtype='float64')pre_grad = np.zeros_like(x)for i in range(50):grad = g(x)pre_grad = pre_grad * discount + grad * stepx -= pre_grad
    print '[ Epoch {0} ] grad = {1}, x = {2}'.format(i, grad, x)if abs(sum(grad)) &lt; 1e-6:break;
return x

可以看出这个算法和之前的梯度下降法相比，唯一不同的就是多了一个pre_grad*discount，这就是动量发挥余热的地方。

那么动量究竟有什么作用呢？今天主要扯它其中的一个作用，那就是帮助你穿越“山谷”。怎么来理解穿越“山谷”呢？先来一个待优化函数。这次的问题相对复杂些，是一个二元二次函数 $z=x^2+50y^2$ ：

def f(x):

return x[0] * x[0] + 50 * x[1] * x[1]

def g(x):

return np.array([2 * x[0], 100 * x[1]])

xi = np.linspace(-200,200,1000)

yi = np.linspace(-100,100,1000)

X,Y = np.meshgrid(xi, yi)

Z = X * X + 50 * Y * Y

上面这个函数在等高线图上是这样的：

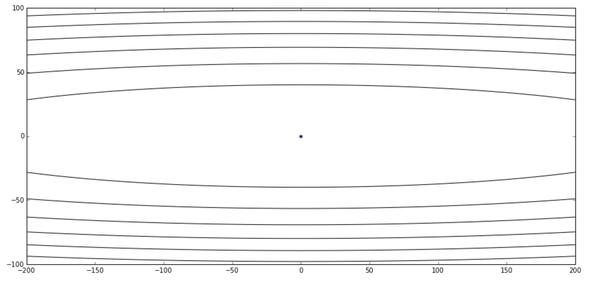
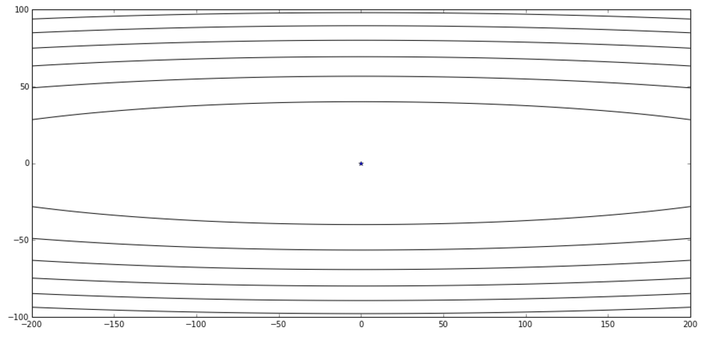
其中中心的蓝色点表示了最优值。我们根据这个图发挥下想象，这个函数在y轴十分陡峭，在x轴相对平缓些。好了话说完我们赶紧拿朴素梯度下降来尝试下：

gd([150,75], 0.016, g)

经过50轮的迭代，他的优化过程图如下所示：

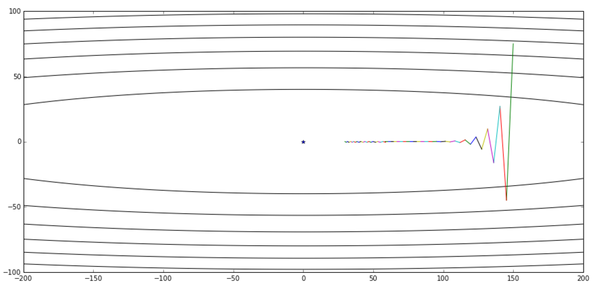
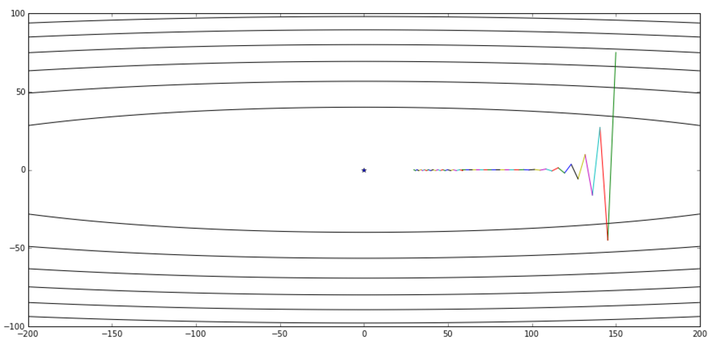
可以看出我们从某个点出发，整体趋势向着最优点前进，这个是没有问题的，但是前进的速度似乎有点乏力，是不是步长又设小了？有了之前的经历，这一回我们在设置步长时变得小心了许多：

res, x_arr = gd([150,75], 0.019, g)

contour(X,Y,Z, x_arr)

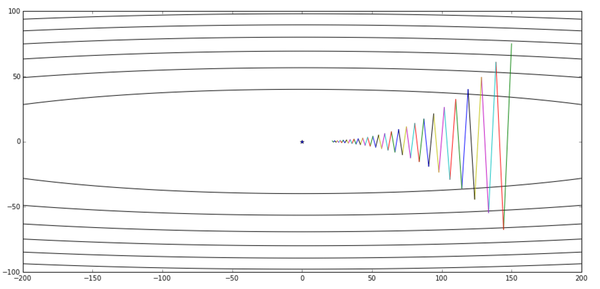
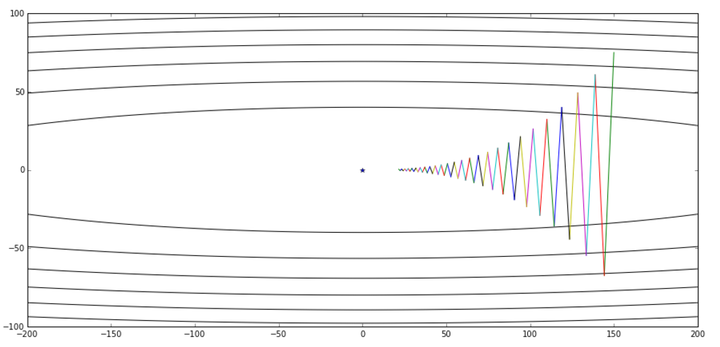
好像成效不是很明显啊，而且优化的过程中左右来回抖是怎么回事？看着这个曲线让我想起了一个极限运动：

（来自网络，如有侵权立即删除）

没错，其实算法眼中的这个函数很这张图很像，而算法也果然没有让大家“失望”，选择了一条艰难的道路进行优化——就像从一边的高台滑下，然后滑到另一边，这样艰难地前进。没办法，这就是梯度下降法。在它的眼中，这样走是最快的，而事实上，每个优化点所对应的梯度方向也确实是那个方向。

大神们这时可能会聊起特征值的问题，关于这些问题以后再说。好吧，现在我们只能继续挑步长，说不定步长再大点，“滑板少年”还能再快点呢！

res, x_arr = gd([150,75], 0.02, g)

contour(X,Y,Z, x_arr)

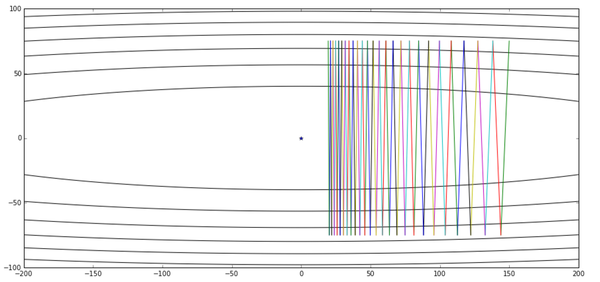
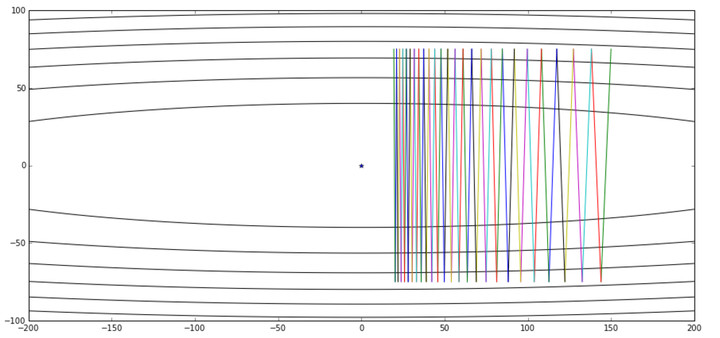
好吧……我们的滑板少年已经彻底玩脱了……这已经是我们能设的最大的步长了（上一次关于步长和函数之间的关系在这里依然受用），再设大些我们的滑板少年就飞出去了。对于这个问题，由于两个坐标轴方向的函数属性不同，为了防止在优化的过程中发散，步长只能够根据最陡峭的方向设定。当然，解决快速收敛这个问题还有其他的办法，这里我们看看冲量如何搞定这位滑板少年。

很自然地，我们在想，要是少年能把行动的力量集中在往前走而不是两边晃就好了。这个想法分两个步骤：首先是集中力量向前走，然后是尽量不要在两边晃。这时候，我们的动量就闪亮登场了。我们发现滑板少年每一次的行动只会在以下三个方向进行：

沿-x方向滑行

沿+y方向滑行
沿-y方向滑行
我们可以想象到，当使用了动量后，实际上沿-y和+y方向的两个力可以相互抵消，而-x方向的力则会一直加强，这样滑板少年会在y方向打转，但是y方向的力量会越来越小，但是他在-x方向的速度会比之前快不少！

好了，那我们看看加了动量技能的滑板少年的实际表现：
```
momentum([150,75], 0.016, g)
```
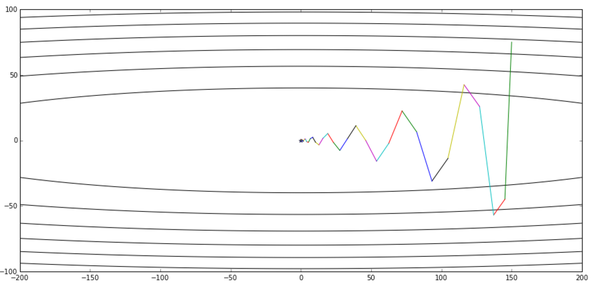
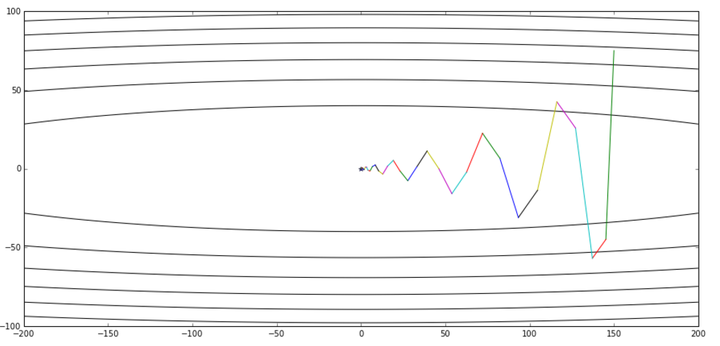
总算没有让大家失望，尽管滑板少年还是很贪玩，但是在50轮迭代后，他还是来到了最优点附近。可以说是基本完成了我们的任务吧。当然由于动量的问题，前面几轮迭代他在y轴上玩得似乎比以前还欢乐，这个问题我们后面会提。但不管怎么说，总算完成目标了。

后来，又有高人发明了解决前面动量没有解决的问题的算法，干脆不让滑板少年愉快地玩耍了，也就是传说中的Nesterov算法。这里就不细说了，有时间详细聊下。直接给出代码和结果：
```
def nesterov(x_start, step, g, discount = 0.7):   x = np.array(x_start, dtype='float64')pre_grad = np.zeros_like(x)for i in range(50):x_future = x - step * discount * pre_gradgrad = g(x_future)pre_grad = pre_grad * 0.7 + grad x -= pre_grad * step
    print '[ Epoch {0} ] grad = {1}, x = {2}'.format(i, grad, x)if abs(sum(grad)) &lt; 1e-6:break;
return x
```
nesterov([150,75], 0.012, g)

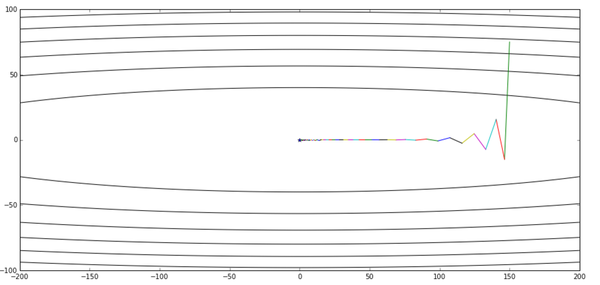
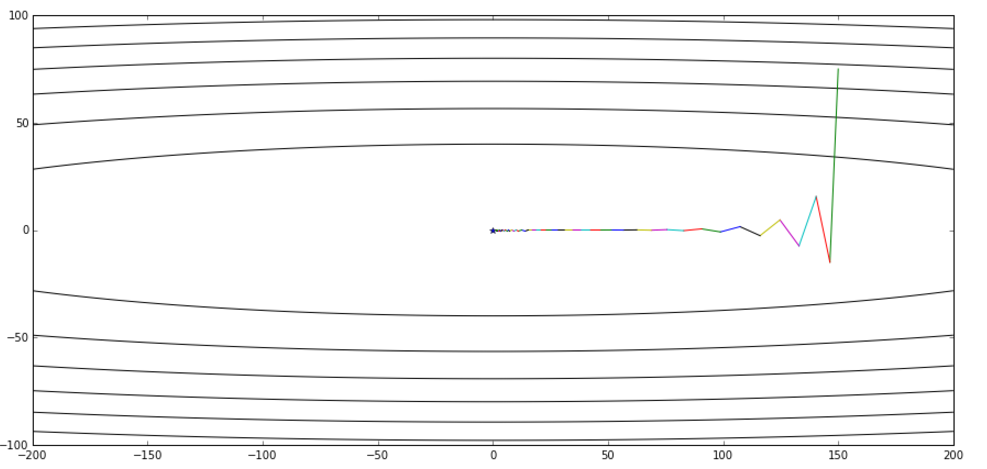
好了，滑板少年已经哭晕在厕所……

费了这么多话，我们总算把穿越“山谷”这件事情说完了，下面还要说一个数值上的事情。在CNN的训练中，我们的开山祖师已经给了我们动量的建议配置——0.9（刚才的例子全部是0.7）,那么0.9的动量有多大量呢？终于要来点公式了……

我们用G表示每一轮的更新量，g表示当前一步的梯度量（方向*步长），t表示迭代轮数， $\gamma$ 表示冲量的衰减程度，那么对于时刻t的梯度更新量有：

那么我们可以计算下对于梯度g0对从G0到GT的总贡献量为

我们发现它的贡献是一个等比数列，如果 $\gamma$ =0.9，那么跟据等比数列的极限运算方法，我们知道在极限状态下，它一共贡献了自身10倍的能量。如果 $\gamma$ =0.99呢？那就是100倍了。

那么在实际中我们需要多少倍的能量呢？

本文相关代码详见：https://github.com/hsmyy/zhihuzhuanlan/blob/master/momentum.ipynb

广告时间

更多精彩尽在《深度学习轻松学：核心算法与视觉实践》！