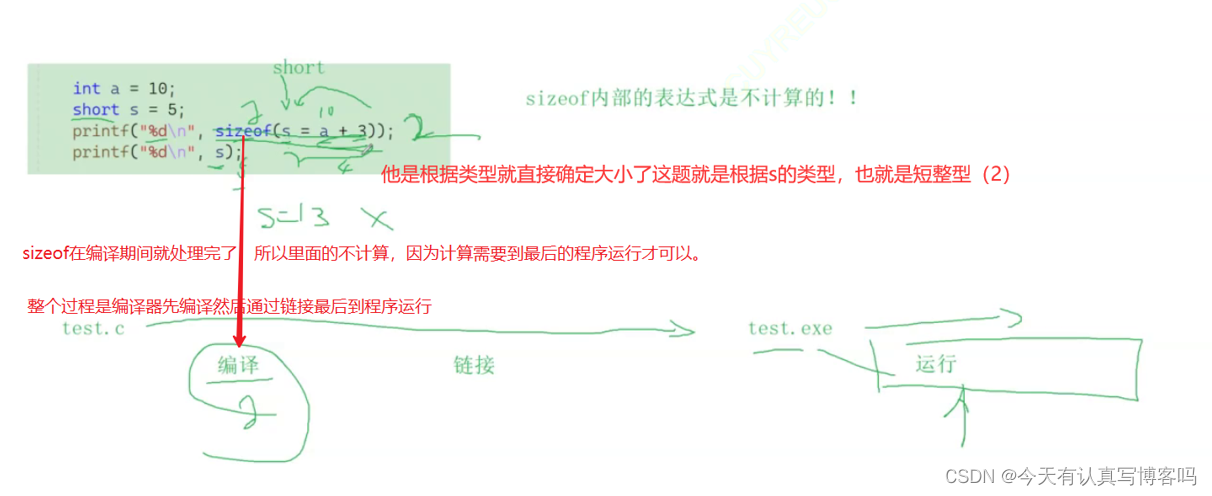
503. 下一个更大元素 II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:

输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:

输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]

提示:

• 1 <= nums.length <= 104
• -109 <= nums[i] <= 109

和739. 每日温度，496.下一个更大元素 I 里下一个更大元素 I 的思路基本一样，把数组复制一份拼接到原数组后，达到类似于循环的效果。或者模拟遍历两次数组，可以节省空间和时间。

class Solution {public int[] nextGreaterElements(int[] nums) {int len = nums.length;int[] res = new int[len];Arrays.fill(res,-1);Deque<Integer> stack = new LinkedList<>();for (int i = 0; i < 2 * len; i++) {while (!stack.isEmpty() && nums[i % len] > nums[stack.peek()]) {res[stack.peek()] = nums[i % len];stack.pop();}stack.push(i % len);}return res;}
}

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

非常经典的一道题目，基本是刷题必刷。可以先试试用双指针完成这道题目。完成这道题目核心在于理解“一只水桶能盛多少水，取决于最短的那块木板” 。本题就可以看成是多个二维的水桶的拼接，接水的高度取决于两侧的“木板”最“短”的那个。需要注意的是取的是两侧的木板最短的，两侧木板中间的高低起伏，只要没高过两侧木板，是不影响水的最大高度的。而如果中间有一块比两侧木板还高的，那我们就不将其看成一个木桶，而是两个木桶的拼接，两个木桶较高的一侧为中间那个更高的柱子。所以思路应该是遍历数组，然后在遍历过程中向右向左遍历，找出当前元素右侧和左侧最高的柱子作为“木桶”的两侧“木板”，取最短的那个作为木桶装水的最大高度，再减去当前柱子的高度，作为当前宽度装水的实际容量。需要注意的是如果遍历到的柱子，其两侧木板都没有自身高，当前宽度装水的容量是0，而不是一个负数。

class Solution {public int trap(int[] height) {int sum = 0;for (int i = 1; i < height.length - 1; i++) {int rHeight = height[i];int lHeight = height[i];for (int r = i + 1; r < height.length; r++) {if (height[r] > rHeight)    rHeight = height[r];}for (int l = i - 1; l >= 0; l--) {if (height[l] > lHeight)    lHeight = height[l];}int h = Math.min(lHeight,rHeight) - height[i];if (h > 0)  sum += h;}return sum;}
}

然后我们发现，在遍历元素的过程中，我们每遍历一个柱子，都往两侧找最高的边，但在遍历其中一个“木桶”时，两侧的最大高度显然是不变的，但我们还是每次都要重找一遍，显然做了很多无用功。虽然可以存储木桶的两侧的值再加一堆判断来简化，但既然都做到这一步了，不如直接动态规划：

class Solution {public int trap(int[] height) {int sum = 0;int len = height.length;int[] maxLeft = new int[len];int[] maxRight = new int[len];maxLeft[0] = height[0];for(int i = 1; i < len; i++) {maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);}maxRight[len - 1] = height[len - 1];for(int i = len - 2; i >= 0; i--) {maxRight[i] = Math.max(height[i], maxRight[i + 1]);}for (int i = 0; i < len; i++) {int count = Math.min(maxLeft[i], maxRight[i]) - height[i];if (count > 0)  sum += count;}return sum;}
}

其中maxLeft和maxRight记录的其实就是当前元素所在的“木桶”的两边的高度。

然后就是单调栈方法。说实话很不好想，而且思路和双指针、动态规划完全不一样。双指针、动态规划的思路是找出“木桶”的两侧再计算“桶”的容积，而单调栈方法类似于“填坑”，也就是出现一个凹陷就计算这个凹陷的容积，再把这个凹陷填上，直至填满所有凹陷，再把这些凹陷的容积相加。单调栈栈底到栈顶应该是由大到小。凹陷的高度取决于三个值，待操作元素（出现比栈顶元素更大的值了！）、栈顶元素、栈顶元素下的元素（把栈底到栈顶视为从左到右，该元素是栈顶的左边的元素），坑的高度为待操作元素和栈顶元素下的元素较小的那个，减去栈顶元素（不算已被填平的坑的高度），坑的宽度为待操作元素-栈顶元素下的元素-1。当然填坑只是比较形象的说法，实际实现并没有什么填坑的操作，只是把已经计算完对应水高度的宽度在计算时忽略掉（已经计算完容积并从栈中弹出）。

class Solution {public int trap(int[] height) {int sum = 0;int len = height.length;Deque<Integer> stack = new LinkedList<>();stack.push(0);for (int i = 1; i < len; i++) {if (height[i] < height[stack.peek()]) {stack.push(i);}else if (height[i] == height[stack.peek()]) {stack.pop();stack.push(i);}else {while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int mid = stack.pop();if (!stack.isEmpty()) {int left = stack.peek();int h = Math.min(height[left], height[i]) - height[mid];int w = i - left - 1;sum += h * w;}}stack.push(i);}}return sum;}
}

精简一下：

class Solution {public int trap(int[] height) {int sum = 0;int len = height.length;Deque<Integer> stack = new LinkedList<>();stack.push(0);for (int i = 1; i < len; i++) {while (!stack.isEmpty() && height[i] > height[stack.peek()]) {int mid = stack.pop();if (!stack.isEmpty()) {int left = stack.peek();int h = Math.min(height[left], height[i]) - height[mid];int w = i - left - 1;sum += h * w;}}stack.push(i);   }return sum;}
}