基于MATLAB实现WSN（无线传感器网络）的LEACH（低能耗自适应集群层次结构）（Matlab代码实现）

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

💥1 概述

低能耗自适应集群层次结构（“LEACH”）是一种基于 TDMA 的 MAC 协议，它与无线传感器网络（WSN）中的集群和简单路由协议集成在一起。LEACH的目标是降低创建和维护集群所需的能耗，以延长无线传感器网络的使用寿命。

LEACH 是一种分层协议，其中大多数节点传输到集群头，集群头聚合和压缩数据并将其转发到基站（接收器）。每个节点在每一轮都使用随机算法来确定它是否会成为这一轮的集群头。LIVEC假设每个节点都有一个足够强大的无线电，可以直接到达基站或最近的集群头，但是一直全功率使用这个无线电会浪费能量。

在 P 轮中，已成为集群头的节点不能再次成为集群头，其中 P 是所需的集群头百分比。此后，每个节点有 1/P 的概率再次成为集群头。在每个轮次结束时，每个不是群集头的节点都会选择最近的群集头并加入该群集。然后，群集头为其群集中的每个节点创建一个计划以传输其数据。

所有不是群集头的节点仅根据群集头创建的计划以 TDMA 方式与群集头通信。他们使用到达集群头所需的最小能量来做到这一点，并且只需要在他们的时间段内保持无线电打开。

LEACH还使用CDMA，以便每个集群使用一组不同的CDMA代码，以尽量减少集群之间的干扰。

📚2 运行结果

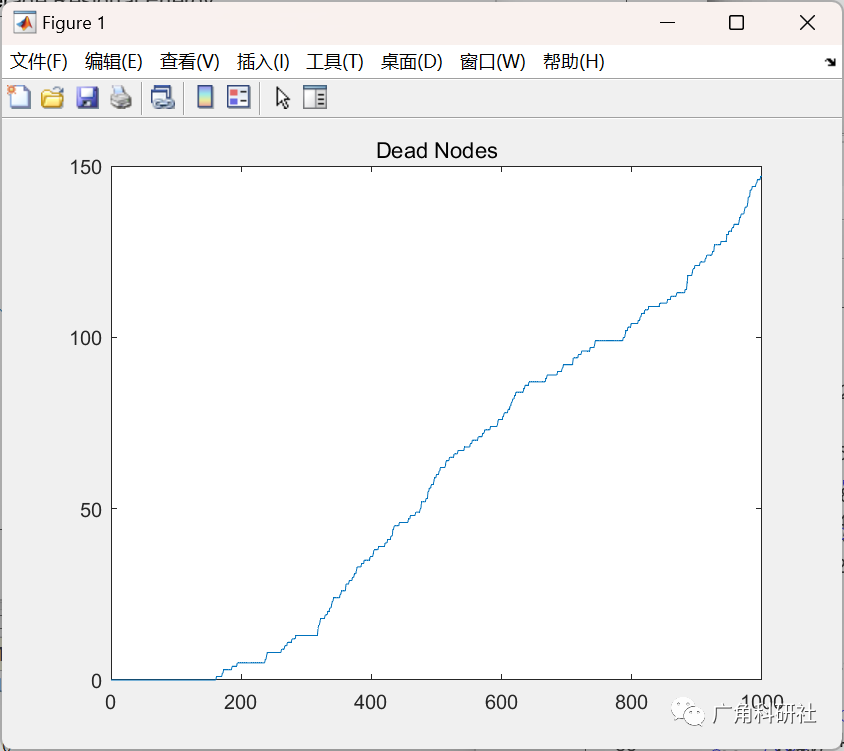
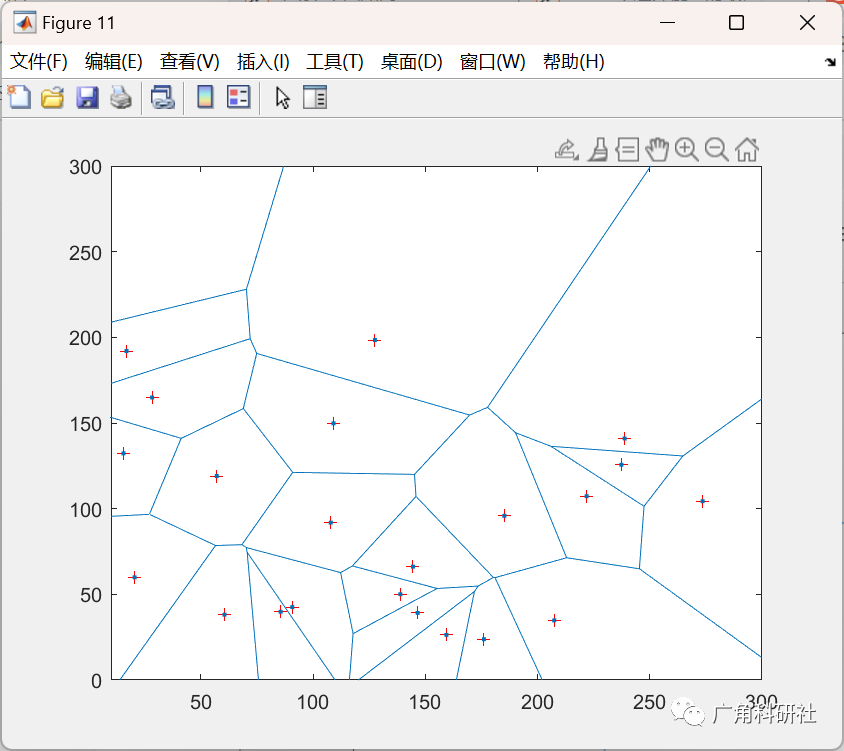
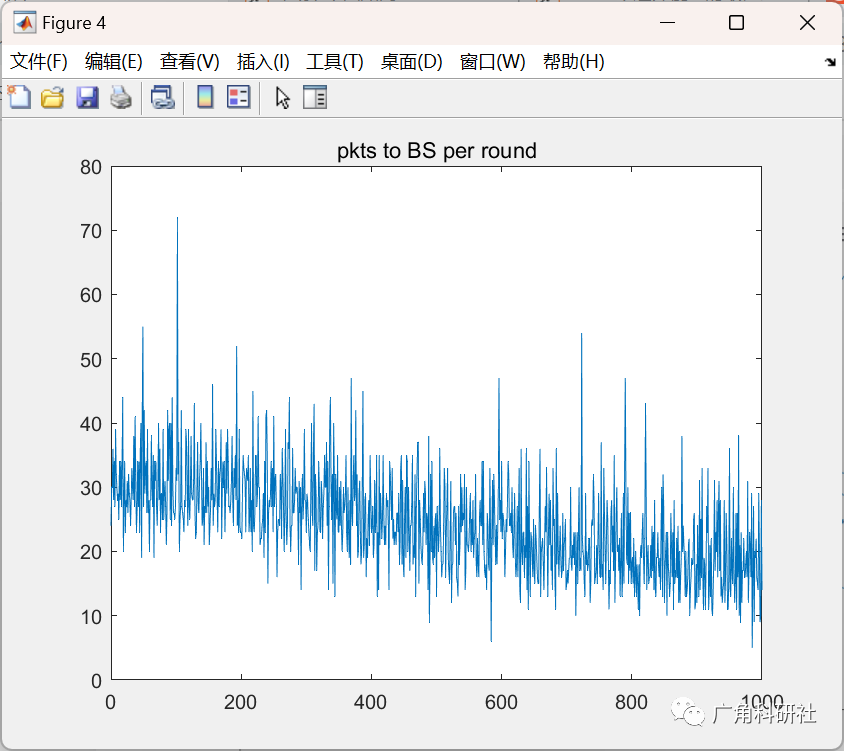
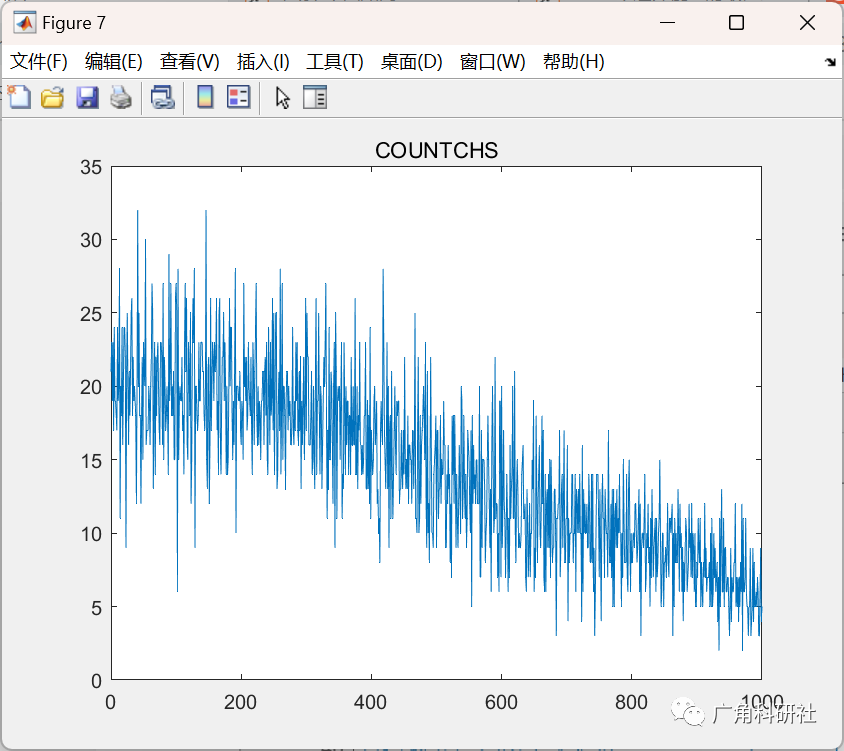
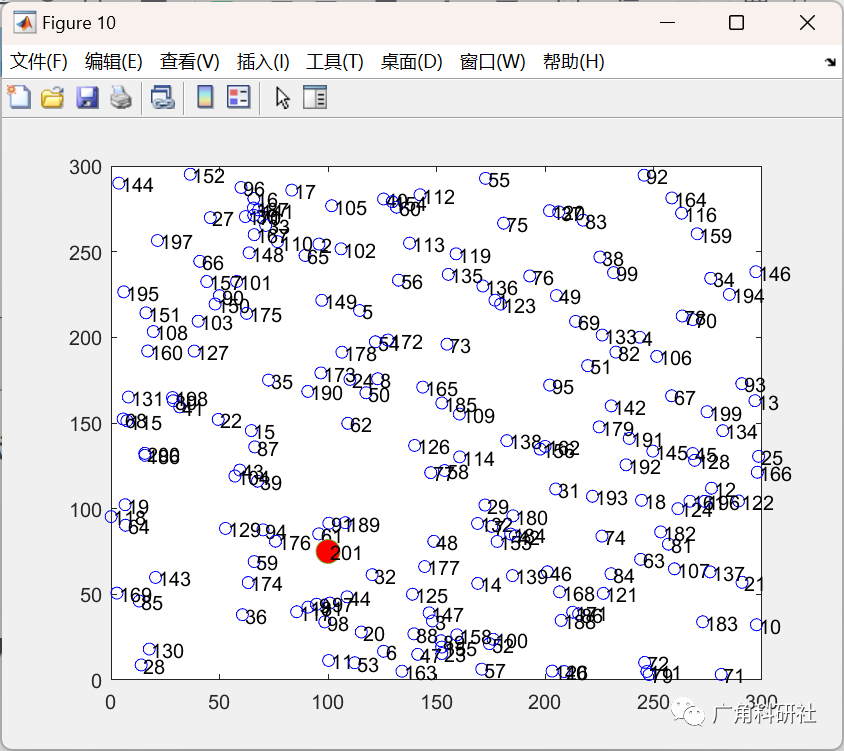
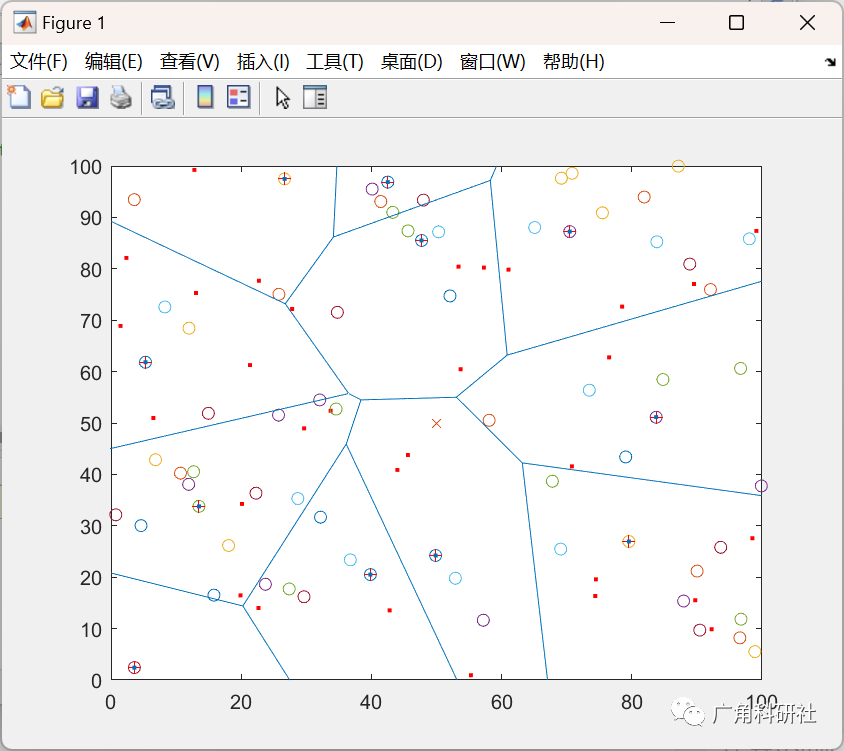
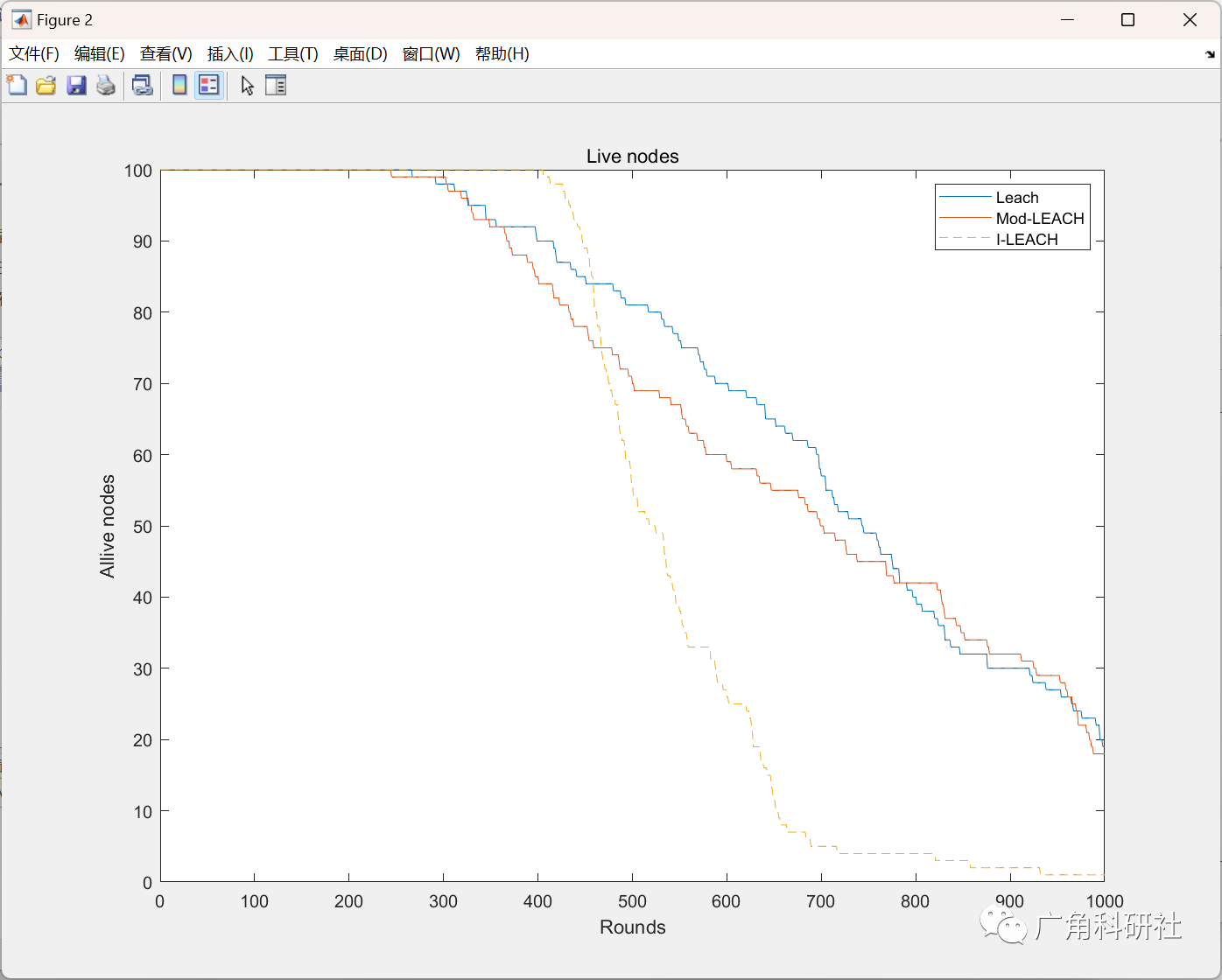
主函数部分代码：

clc
clear all;
close all;
xm=300;
ym=300;
sink.x=0.5*xm;
sink.y=0.5*ym;
sink.x=100;
sink.y=75;

n=200;
p=0.1;
Eo=0.5;
ETX=50*0.000000001;
ERX=50*0.000000001;
Efs=10e-12;
Emp=0.0013e-12;
EDA=5*0.000000001;
rmax=1000;
do=sqrt(Efs/Emp);
Et=0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%                           LEACH                               %%%%%%%%
%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%%
%%   
for h=1:1S(n+1).xd=sink.x;S(n+1).yd=sink.y;Et=0;
for i=1:1:nS(i).xd=rand(1,1)*xm;XR(i)=S(i).xd;S(i).yd=rand(1,1)*ym;YR(i)=S(i).yd;distance=sqrt( (S(i).xd-(S(n+1).xd) )^2 + (S(i).yd-(S(n+1).yd) )^2 );S(i).distance=distance;S(i).G=0;%
initially there are no cluster heads only nodes    S(i).type='N';S(i).E=Eo;Et=Et+S(i).E;figure(h*10)plot(S(i).xd,S(i).yd,'bo');text(S(i).xd+1,S(i).yd-0.5,num2str(i));hold on;
end

plot(S(n+1).xd,S(n+1).yd,'o', 'MarkerSize', 12, 'MarkerFaceColor', 'r');
text(S(n+1).xd+1,S(n+1).yd-0.5,num2str(n+1));
hold off ;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
countCHs=0;  %variable, counts the cluster head
cluster=1;  %cluster is initialized as 1
flag_first_dead=0; %flag tells the first node dead
flag_half_dead=0;  %flag tells the 10th node dead
flag_all_dead=0;  %flag tells all nodes dead
first_dead=0;
half_dead=0;
all_dead=0;
allive=n;
%counter for bit transmitted to Bases Station and to Cluster Heads
packets_TO_BS=0;
packets_TO_CH=0;
packets_TO_BS_per_round=0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for r=0:1:rmaxr packets_TO_BS_per_round=0;%Operations for epochsif(mod(r, round(1/p) )==0)for i=1:1:nS(i).G=0;S(i).cl=0;endend%hold off;%Number of dead nodesdead=0;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for i=1:1:n%
checking 
ifthere is a dead node        if (S(i).E<=0)%plot(S(i).xd,S(i).yd,'red .');dead=dead+1;if (dead==1)if(flag_first_dead==0)first_dead=r;flag_first_dead=1;endendif(dead==0.5*n)if(flag_half_dead==0)half_dead=r;flag_half_dead=1;endend