4.7排序(C语言)

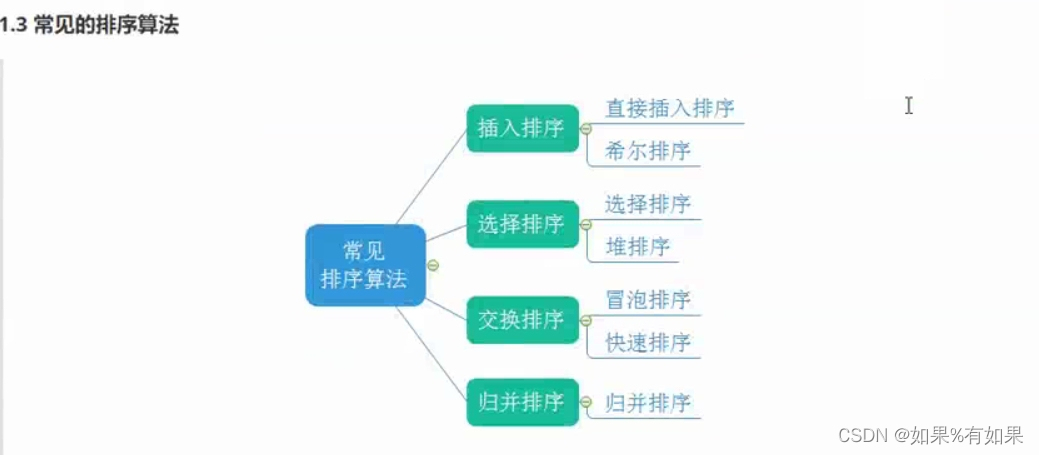
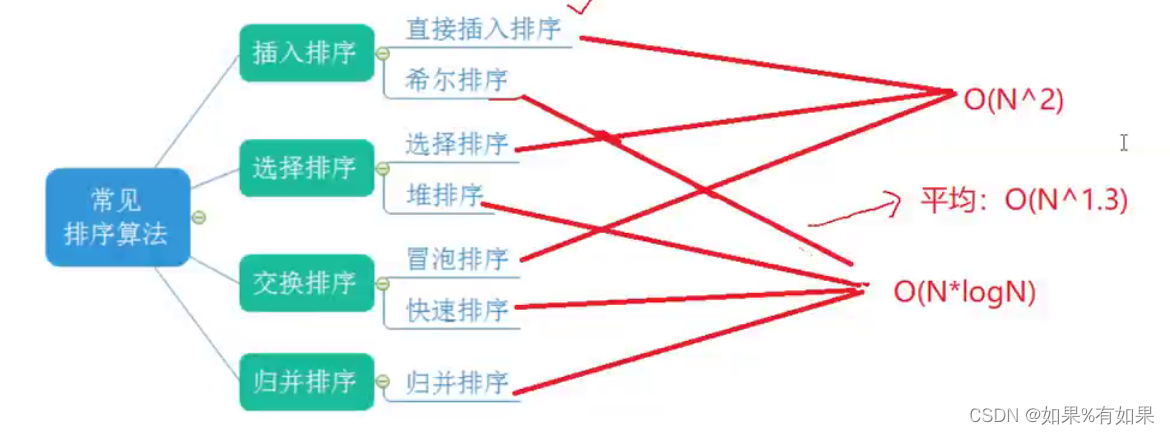
1.八大排序

加一个计数排序（时间复杂度为O(n)，空间复杂度为O(max(n, range)，非比较排序）。

2.希尔排序

3.三个O(n^2)的排序的比较

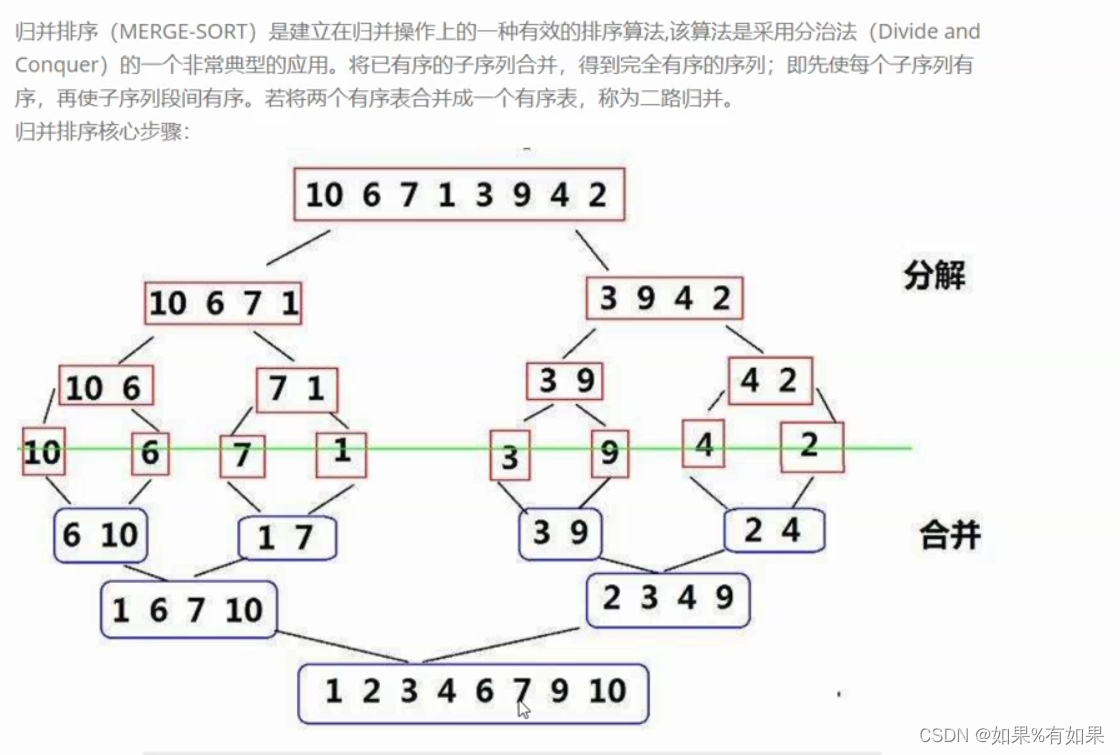
4.归并排序和快速排序

非递归：

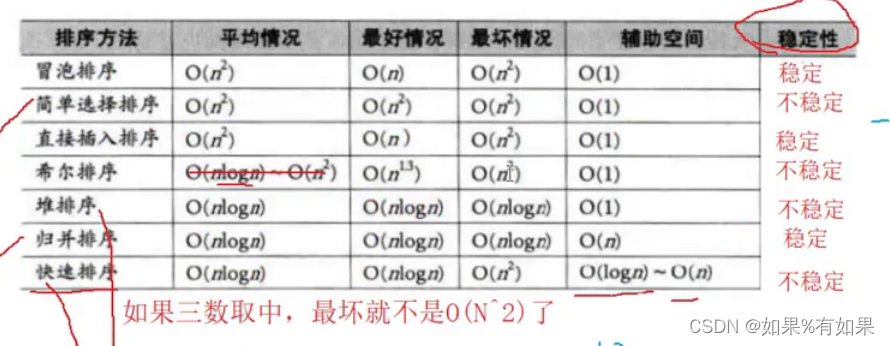
5.排序比较

注意：下面4种高效排序中，综合性能最好的是快速排序，但是在全都是一个相同的数的情况下，快排的效率最低，因为它无法分成大小区间，在实际中，希尔排序用的比较少，它是数据越多，越无序，优势越明显，但是面对少量数据优势就变成了劣势，归并排序空间复杂度较高，堆排序要先建堆，精确的时间复杂度是O(n + nlogn)。具体效率见下图：

1.1 十万个随机数Debug模式下：

1.2 十万个随机数Release模式下：

2.1 百万个随机数Debug模式下：

2.2 百万个随机数Release模式下：

3.1 千万个随机数Debug模式下：

3.2 千万个随机数Release模式下：

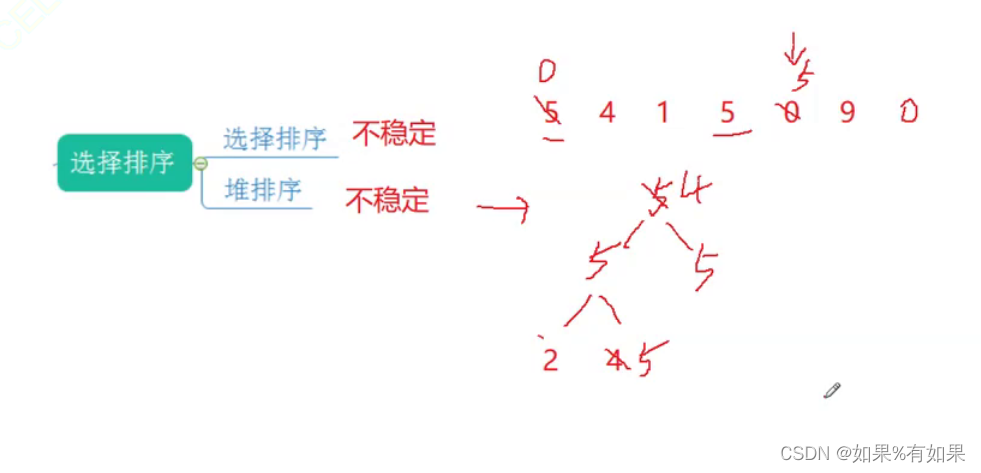
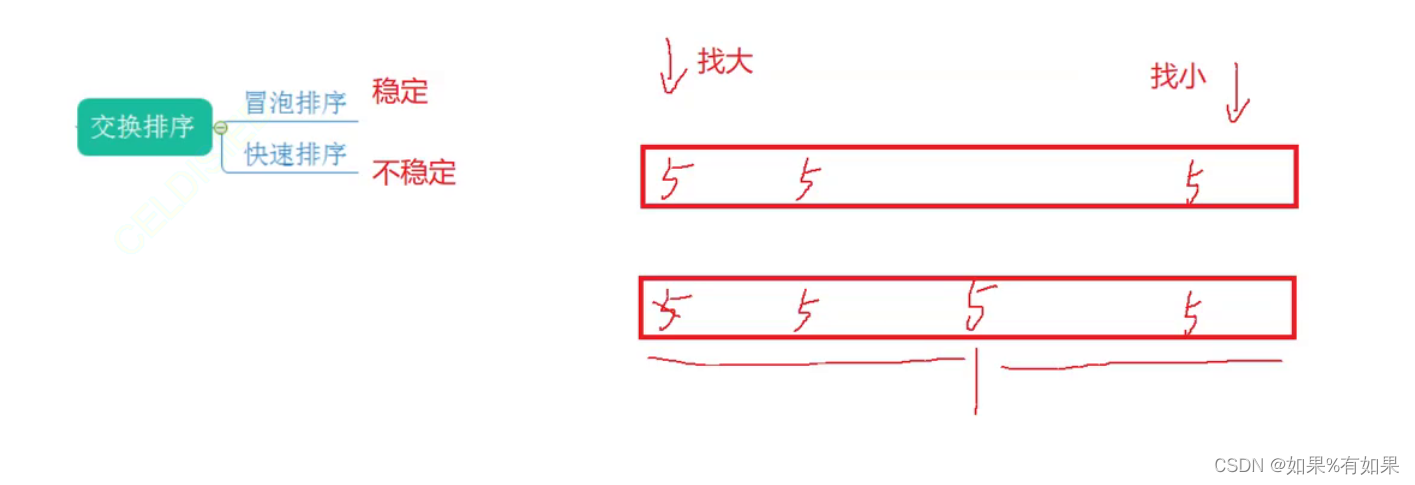
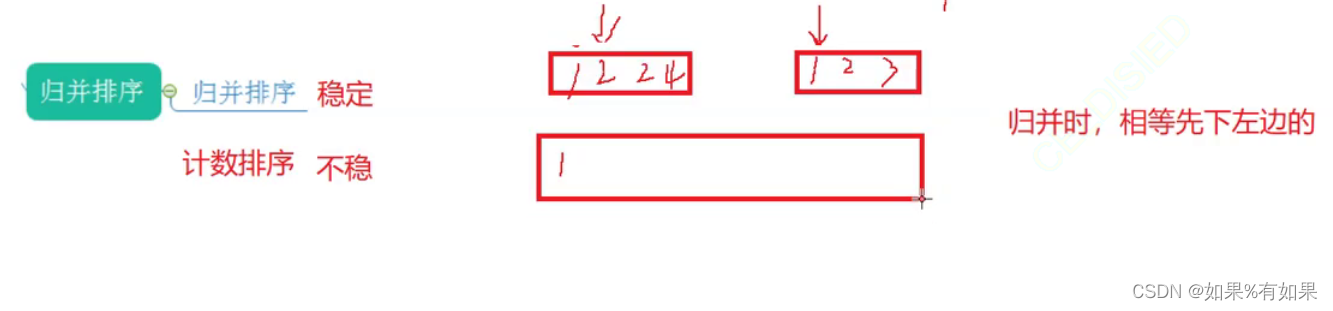
6.稳定型：

数组中相同的值，在排序之后相对位置是否变化，如果可能会变，就是不稳定的，不变就是稳定的。

所有的排序都可以不稳定。

7.堆排序参考以下博客：

4.6.2二叉树（堆和堆排序）（C语言）

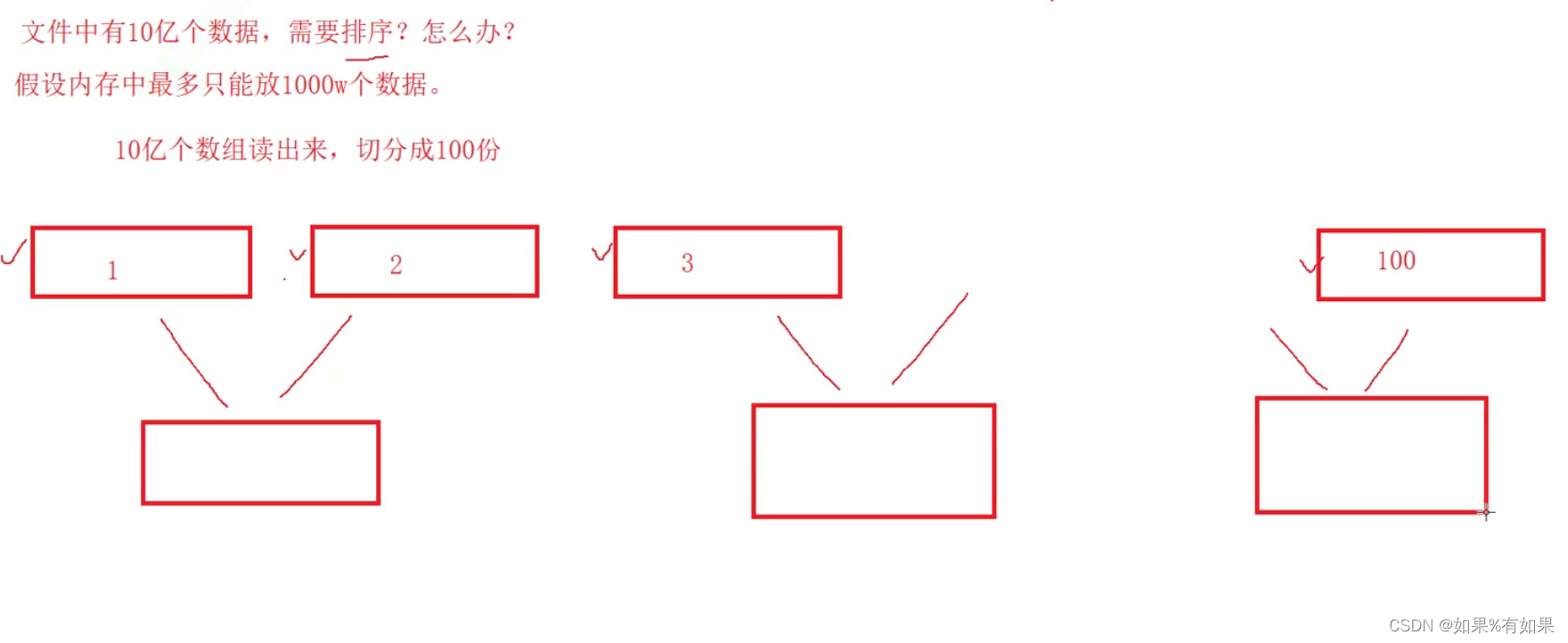
8.内排序和外排序

9.我的代码：

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int STDataType;     //重定义数据类型
typedef struct Stack
{STDataType* data;int top;                //栈顶int capacity;           //容量
}Stack;extern void StackInit(Stack* ps);                         // 1.初始化栈 extern void StackPush(Stack* ps, STDataType x);           // 2.入栈 extern void StackPop(Stack* ps);                          // 3.出栈 extern STDataType StackTop(Stack* ps);                    // 4.获取栈顶元素 extern int StackSize(Stack* ps);                          // 5.获取栈中有效元素个数 extern bool StackEmpty(Stack* ps);                        // 6.检测栈是否为空extern void StackDestroy(Stack* ps);                      // 7.销毁栈

#include"Stack.h"void StackInit(Stack* ps)     // 1.初始化栈 
{assert(ps);ps->data = NULL;ps->capacity = 0;ps->top = 0;     //初始值是－1或0都可以，但是初始值不同，后期的操作不同}void StackPush(Stack* ps, STDataType x)     // 2.入栈 
{assert(ps);if (ps->capacity == ps->top)     //扩容{int newcapacity = ps->capacity > 0 ? 2 * ps->capacity : 4;     //考虑容量为0的情况STDataType* tmp = (STDataType*)realloc(ps->data, sizeof(STDataType) * newcapacity);if (tmp == NULL)     //考虑扩容失败{perror("realloc:");return;}ps->data = tmp;ps->capacity = newcapacity;}ps->data[ps->top] = x;ps->top++;
}void StackPop(Stack* ps)     // 3.出栈
{assert(ps);assert(!StackEmpty(ps));     //考虑栈空ps->top--;
}STDataType StackTop(Stack* ps)     // 4.获取栈顶元素 
{assert(ps);assert(!StackEmpty(ps));     //考虑栈空return ps->data[ps->top - 1];
}int StackSize(Stack* ps)     // 5.获取栈中有效元素个数 
{assert(ps);return ps->top;
}bool StackEmpty(Stack* ps)         // 6.检测栈是否为空
{assert(ps);return ps->top == 0;
}void StackDestroy(Stack* ps)     // 7.销毁栈 
{assert(ps);free(ps->data);ps->data = NULL;ps->capacity = 0;ps->top = 0;
}

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<windows.h>
#include<string.h>typedef int dataType;// 打印
extern void PrintArray(dataType* a, int n);
// 插入排序
extern void InsertSort(dataType* a, int n);// 希尔排序
extern void ShellSort(dataType* a, int n);// 选择排序
extern void SelectSort(dataType* a, int n);// 冒泡排序
extern void BubbleSort(dataType* a, int n);// 堆排序
extern void HeapSort(dataType* a, int n);// 快速排序
extern void QuickSort(dataType* a, int left, int right);// 快速排序非递归
extern void QuickSortNonR(dataType* a, int left, int right);// 归并排序递归
extern void MergeSort(dataType* a, int n);// 归并排序非递归
extern void MergeSortNonR(dataType* a, int n);// 计数排序
extern void CountSort(dataType* a, int n);

#include"Sort.h"
#include"Stack.h"//交换两个数
void swap(dataType* pa, dataType* pb)
{int tmp = *pa;*pa = *pb;*pb = tmp;
}
// 打印
void PrintArray(dataType* a, int n)
{assert(a);for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}// 插入排序
void InsertSort(dataType* a, int n)
{assert(a);for (int i = 0; i < n - 1; ++i){int end = i;int x = a[end + 1];while (end >= 0){if (x < a[end]){a[end + 1] = a[end];--end;}else{break;}}a[end + 1] = x;}
}// 希尔排序
void ShellSort(dataType* a, int n)
{int gap = n;//多次预排while (gap > 1) {//确保最后一次gap是1//gap = gap / 3 + 1;gap = gap / 2;//一锅炖，一步到位for (int i = 0; i < n - gap; i++){int end = i;int x = a[end + gap];while (end >= 0){if (x < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = x;}}
}// 选择排序
void SelectSort(dataType* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int iMax = begin;int iMin = end;//记录最大和最小的位置for (int i = begin; i <= end; ++i){if (a[i] > a[iMax]){iMax = i;}if (a[i] < a[iMin]){iMin = i;}}swap(&a[iMin], &a[begin]);//考虑特殊情况，当最大值在第一个的时候，第一次交换会被换到最小值的位置if (iMax == begin){iMax = iMin;}swap(&a[iMax], &a[end]);++begin;--end;}
}//向下调整
void adjustDown(dataType* a, int n, int iParent)
{//假设左孩子大int iChild = iParent * 2 + 1;while (iChild < n){//如果右孩子大if (iChild + 1 < n && a[iChild + 1] > a[iChild]){++iChild;}if (a[iChild] > a[iParent]){swap(&a[iChild], &a[iParent]);iParent = iChild;iChild = iParent * 2 + 1;}else{break;}}
}// 堆排序
void HeapSort(dataType* a, int n)
{//先建立一个堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){adjustDown(a, n, i);}//堆顶元素和最后一个元素交换，剩下的继续向下调整int iEnd = n - 1;while (iEnd != 0){adjustDown(a, iEnd + 1, 0);swap(&a[0], &a[iEnd]);--iEnd;}
}// 冒泡排序
void BubbleSort(dataType* a, int n)
{int end = n;while (end > 0){int flag = 0;for (int j = 1; j < end; ++j){if (a[j - 1] > a[j]){swap(&a[j - 1], &a[j]);flag = 1;}}if (flag == 0){break;}--end;}
}//快排优化，三数取中
int getMidIndex(int* a, int left, int right)
{int iMid = left + ((right - left) >> 1);if (a[left] > a[iMid]){if (a[right] >= a[left]){return left;}else{return a[right] > a[iMid] ? right : iMid;}}else //a[left] <= a[iMid]{if (a[right] >= a[iMid]){return iMid;}else{return a[left] > a[right] ? left : right;}}
}// 一次快排，左右指针法
int partSort1(int* a, int left, int right)
{//三数取中作为keyint mid = getMidIndex(a, left, right);int iKey = left;swap(&a[iKey], &a[mid]);while (left < right){//先从右边开始找小while (left < right && a[iKey] <= a[right]){--right;}//再从左边找大while (left < right && a[iKey] >= a[left]){++left;}//交换swap(&a[left], &a[right]);}//最后和iKey位置交换swap(&a[left], &a[iKey]);return left;
}//一次快排，挖坑法
int partSort2(int* a, int left, int right)
{//三数取中作为keyint mid = getMidIndex(a, left, right);int dig = left;swap(&a[dig], &a[mid]);//保存dig的值int key = a[dig];while (left < right){//右边找小，和坑交换，并且作为新的坑while (left < right && a[right] >= key){--right;}a[dig] = a[right];dig = right;//左边找大，和坑交换，并且作为新的坑while (left < right && a[left] <= key){++left;}a[dig] = a[left];dig = left;}a[dig] = key;return dig;
}//一次快排，前后指针法
int partSort3(int* a, int left, int right)
{int mid = getMidIndex(a, left, right);swap(&a[left], &a[mid]);int cur = left + 1;int prev = left;while (cur <= right){//方法1/*while (cur <= right && a[cur] >= a[left]){++cur;}if (cur <= right){++prev;swap(&a[cur], &a[prev]);++cur;}*///方法2if (a[cur] < a[left] && ++prev != cur){swap(&a[cur], &a[prev]);}++cur;}swap(&a[prev], &a[left]);return prev;
}// 快速排序
void QuickSort(dataType* a, int left, int right)
{if (left >= right){return;}//小区间优化，使用直接插入排序if (right - left + 1 < 10){InsertSort(a + left, right - left + 1);}//定义中间位置iKeyint iKey = partSort3(a, left, right);//处理中间位置的左边QuickSort(a, left, iKey - 1);QuickSort(a, iKey + 1, right);
}// 快速排序非递归
void QuickSortNonR(dataType* a, int left, int right)
{//使用栈存储区间Stack st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (!StackEmpty(&st)){int end = StackTop(&st);//注意出栈的顺序StackPop(&st);int begin = StackTop(&st);StackPop(&st);int iKey = partSort3(a, begin, end);//[begin, iKey - 1] iKey [iKey + 1, end]if (iKey + 1 < end){StackPush(&st, iKey + 1);StackPush(&st, end);}if (begin < iKey - 1){StackPush(&st, begin);StackPush(&st, iKey - 1);}}StackDestroy(&st);
}//归并排序递归法
void _MergeSort(dataType* a, int left, int right, dataType* tmp)
{if (left >= right){return;}int mid = (left + right) / 2;//[left, mid] [mid + 1, right]_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int i = left;//比较，将小的放入临时数组中while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i] = a[begin1];i++;begin1++;}else{tmp[i] = a[begin2];i++;begin2++;}}//处理尾巴//以下两个循环只会进一个while (begin1 <= end1){tmp[i] = a[begin1];i++;begin1++;}while (begin2 <= end2){tmp[i] = a[begin2];i++;begin2++;}//将tmp数组中的有序数组拷贝回原数组for (int j = left; j <= right; j++){a[j] = tmp[j];}
}// 归并排序
void MergeSort(dataType* a, int n)
{dataType* tmp = (dataType*)malloc(sizeof(dataType) * n);if (tmp == NULL){perror("malloc:");exit(-1);}int left = 0;int right = n - 1;_MergeSort(a, left, right, tmp);free(tmp);tmp = NULL;
}// 归并排序非递归
void MergeSortNonR(dataType* a, int n)
{dataType* tmp = (dataType*)malloc(sizeof(dataType) * n);if (tmp == NULL){perror("malloc:");exit(-1);}//gap是一个区间的元素个数int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){//[i, i + gap - 1] [i + gap, i + 2 * gap - 1]int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = i;//三种边界情况处理//1.end2越界，此时[begin2, end2]区间不存在if (end1 >= n){end1 = n - 1;}//2.begin2和end2越界//给个不存在的区间，避免重复录入数据if (begin2 >= n){begin2 = n;end2 = n - 1;}//3.end2越界if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[j] = a[begin1];++j;++begin1;}else{tmp[j] = a[begin2];++j;++begin2;}}//end whilewhile (begin1 <= end1){tmp[j] = a[begin1];++j;++begin1;}while (begin2 <= end2){tmp[j] = a[begin2];++j;++begin2;}}//end for//拷回原数组for (int i = 0; i < n; ++i){a[i] = tmp[i];}gap *= 2;}//end whilefree(tmp);tmp = NULL;
}// 计数排序
void CountSort(dataType* a, int n)
{//先找到最大值和最小值确定范围int max = a[0];int min = a[0];for (int i = 1; i < n; ++i){if (a[i] > max){max = a[i];}if (a[i] < min){min = a[i];}}int count = max - min + 1;dataType* tmp = (dataType*)malloc(sizeof(dataType) * count);if (tmp == NULL){perror("malloc:");exit(-1);}//数组全置0memset(tmp, 0, sizeof(dataType) * count);//保存数据个数for (int i = 0; i < n; ++i){tmp[a[i] - min]++;}//写入原数组int j = 0;for (int i = 0; i < count; ++i){int k = tmp[i];//写入重复的数据while (k-- != 0){a[j] = i + min;++j;}}free(tmp);tmp = NULL;
}

#include"Sort.h"void testInsertSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };InsertSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testShellSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };ShellSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testSelectSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };SelectSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testHeapSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testBubbleSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };BubbleSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testQuickSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };int n = sizeof(arr) / sizeof(arr[0]);QuickSort(arr, 0, n - 1);PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testQuickSortNonR()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };int n = sizeof(arr) / sizeof(arr[0]);QuickSortNonR(arr, 0, n - 1);PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testMergeSort()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };int n = sizeof(arr) / sizeof(arr[0]);MergeSort(arr, n);PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testMergeSortNonR()
{dataType arr[10] = { 5, 6, 4, 2, 8, 3, 7, 9, 1, 0 };int n = sizeof(arr) / sizeof(arr[0]);MergeSortNonR(arr, n);PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}void testCountSort()
{dataType arr[14] = { 5, 6, 4, 2, 8, 3, 5, 5, 8, 6, 7, 9, 1, 0 };int n = sizeof(arr) / sizeof(arr[0]);CountSort(arr, n);PrintArray(arr, sizeof(arr) / sizeof(arr[0]));
}
void test()
{//testInsertSort();//testShellSort();//testSelectSort();//testHeapSort();//testBubbleSort();//testQuickSort();//testQuickSortNonR();//testMergeSort();//testMergeSortNonR();//testCountSort();
}//产生随机数
void getRandomNumber(dataType* array, int n)
{for (int i = 0; i < n; ++i){array[i] = rand();}
}//使用随机数测试性能
void testAll(int n)
{dataType* array = (dataType*)malloc(sizeof(dataType) * n);double begin = 0;double end = 0;/*getRandomNumber(array, n);begin = GetTickCount();InsertSort(array, n);end = GetTickCount();printf("直接插入排序：%.lfms\n", end - begin);*/getRandomNumber(array, n);begin = GetTickCount();ShellSort(array, n);end = GetTickCount();printf("希尔排序：%.lfms\n", end - begin);/*getRandomNumber(array, n);begin = GetTickCount();SelectSort(array, n);end = GetTickCount();printf("直接选择排序：%.lfms\n", end - begin);*/getRandomNumber(array, n);begin = GetTickCount();HeapSort(array, n);end = GetTickCount();printf("堆排序：%.lfms\n", end - begin);/*getRandomNumber(array, n);begin = GetTickCount();BubbleSort(array, n);end = GetTickCount();printf("冒泡排序：%.lfms\n", end - begin);*/getRandomNumber(array, n);begin = GetTickCount();QuickSort(array, 0, n - 1);end = GetTickCount();printf("快速排序递归法：%.lfms\n", end - begin);getRandomNumber(array, n);begin = GetTickCount();QuickSortNonR(array, 0, n - 1);end = GetTickCount();printf("快速排序非递归：%.lfms\n", end - begin);getRandomNumber(array, n);begin = GetTickCount();MergeSort(array, n);end = GetTickCount();printf("归并排序递归：%.lfms\n", end - begin);getRandomNumber(array, n);begin = GetTickCount();MergeSortNonR(array, n);end = GetTickCount();printf("归并排序非递归：%.lfms\n", end - begin);getRandomNumber(array, n);begin = GetTickCount();CountSort(array, n);end = GetTickCount();printf("计数排序：%.lfms\n", end - begin);
}int main()
{//test();srand((unsigned)time(NULL));testAll(10000000);system("pause");return 0;
}

10答案代码：

// 插入排序
void InsertSort(int* a, int n);// 希尔排序
void ShellSort(int* a, int n);void InsertSort(int* a, int n)
{assert(a);//最后一次，是要把n - 1这个数进行排序，则已经//排好序的尾部为n - 2for (int i = 0; i < n-1; ++i){//end表示已经排好序的尾标int end = i;//首先保存要排序的数，一会就会被覆盖了int tmp = a[end + 1];//只要前面的数大于end + 1,则前面的这些数都向后挪动一个位置while (end >= 0 && a[end] > tmp){a[end + 1] = a[end];--end;}a[end + 1] = tmp;}
}void TestInsertSort()
{int a[] = { 3, 4, 6, 1, 2, 8, 3, 5, 7 };InsertSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void ShellSort(int* a, int n)
{assert(a);int gap = n;//不能写成大于0,因为gap的值始终>=1while (gap > 1){//只有gap最后为1，才能保证最后有序//所以这里要加1gap = gap / 3 + 1;//这里只是把插入排序的1换成gap即可//但是这里不是排序完一个分组，再去//排序另一个分组，而是整体只过一遍//这样每次对于每组数据只排一部分//整个循环结束之后，所有组的数据排序完成for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0 && a[end] > tmp){a[end + gap] = a[end];end -= gap;}a[end + gap] = tmp;}}
}void TestShellSort()
{int a[] = { 3, 4, 6, 1, 2, 8, 3, 5, 7 };ShellSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}// 冒泡排序
void BubbleSort(int* a, int n)// 快速排序递归实现
// 快速排序hoare版本
int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
int PartSort3(int* a, int left, int right);
void QuickSort(int* a, int left, int right);// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}void BubbleSort(int* a, int n)
{assert(a);int end = n;while (end > 0){/*加一个标记，如果中间没有发生交换说明前面的值都比后面的小即本身就是有序的，最好的情况下，它的时间复杂度就为N*/int flag = 0;for (int i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);flag = 1;}}if (flag == 0){break;}--end;}
}void TestBubbleSort()
{int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };BubbleSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}// 三数取中法，三个中取一个中间值int GetMidIndex(int* a, int begin, int end)
{int mid = begin + ((end - begin) >> 1);if (a[begin] < a[mid]){if (a[mid] < a[end]){return mid;}else if (a[begin] > a[end]){return begin;}else{return end;}}else // begin >= mid{if (a[mid] > a[end]){return mid;}else if (a[begin] < a[end]){return begin;}else{return end;}}}int PartSort1(int* a, int begin, int end)
{int midindex = GetMidIndex(a, begin, end);Swap(&a[begin], &a[midindex]);int key = a[begin];int start = begin;/*这里要从右边走，如果从左边走，可能最后一步，如果找不到大于基准值的，会导致begin == end即相遇，但是右边还没有走，所以这里的值一定大于基准值，最后交换就会出问题，所以一定要从右边走，即使最后一次找不到小于基准值的，会和左边相遇，而左边此时还没走，一定比基准值小，最后交换肯定没有问题*/while (begin < end){// end 找小while (begin < end && a[end] >= key)--end;// begin找大while (begin < end && a[begin] <= key)++begin;Swap(&a[begin], &a[end]);}//最后的交换一定要保证a[begin] < a[start], 所以要从右边走Swap(&a[begin], &a[start]);return begin;
}int PartSort2(int* a, int begin, int end)
{//begin是坑int key = a[begin];while (begin < end){while (begin < end && a[end] >= key)--end;// end给begin这个坑，end就变成了新的坑。a[begin] = a[end];while (begin < end && a[begin] <= key)++begin;// end给begin这个坑，begin就变成了新的坑。a[end] = a[begin];}a[begin] = key;return begin;
}/*
前后指针法
*/
int PartSort3(int* a, int begin, int end)
{int midindex = GetMidIndex(a, begin, end);Swap(&a[begin], &a[midindex]);int key = a[begin];int prev = begin;int cur = begin + 1;while (cur <= end){// cur找小，把小的往前翻，大的往后翻if (a[cur] < key && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[begin], &a[prev]);return prev;
}// []
void QuickSort(int* a, int left, int right)
{if (left >= right)return;if (right - left + 1 < 10){InsertSort(a+left, right - left + 1);}else{int div = PartSort3(a, left, right);//[left, div-1]//[div+1, right]QuickSort(a, left, div - 1);QuickSort(a, div + 1, right);}
}
//用栈模拟递归，用队列也可以实现
void QuickSortR(int* a, int left, int right)
{Stack st;StackInit(&st, 10);//先入大区间if (left < right){StackPush(&st, right);StackPush(&st, left);}//栈不为空，说明还有没处理的区间while (StackEmpty(&st) != 0){left = StackTop(&st);StackPop(&st);right = StackTop(&st);StackPop(&st);//快排单趟排序int div = PartSort1(a, left, right);// [left div-1]// 把大于1个数的区间继续入栈if (left < div - 1){StackPush(&st, div - 1);StackPush(&st, left);}// [div+1, right]if (div+1 < right){StackPush(&st, right);StackPush(&st, div + 1);}}}void TestQuickSort()
{int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };QuickSortR(a, 0, sizeof(a) / sizeof(int)-1);PrintArray(a, sizeof(a) / sizeof(int));
}// 归并排序递归实现
void MergeSort(int* a, int n)
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)// 计数排序
void CountSort(int* a, int n)
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = left + ((right - left) >> 1);// [left, mid]// [mid+1, right]_MergeSort(a, left, mid, tmp);_MergeSort(a, mid+1, right, tmp);int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a+left, tmp+left, sizeof(int)*(right - left+1));
}void MergeSort(int* a, int n)
{assert(a);int* tmp = (int*)malloc(sizeof(int)*n);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}/*
非递归排序与递归排序相反，将一个元素与相邻元素构成有序数组，
再与旁边数组构成有序数组，直至整个数组有序。
要有mid指针传入，因为不足一组数据时，重新计算mid划分会有问题
需要指定mid的位置
*/
void merge(int* a, int left, int mid, int right, int* tmp)
{// [left, mid]// [mid+1, right]int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a+left, tmp+left, sizeof(int)*(right - left+1));
}/*
k用来表示每次k个元素归并
*/
void mergePass(int *arr, int k, int n, int *temp)
{int i = 0;//从前往后,将2个长度为k的子序列合并为1个while(i < n - 2*k + 1){merge(arr, i, i + k - 1, i + 2*k - 1, temp);i += 2*k;}//合并区间[i, n - 1]有序的左半部分[i, i + k - 1]以及不及一个步长的右半部分[i + k, n - 1]if(i < n - k ){merge(arr, i, i + k - 1,n-1, temp);}}// 归并排序非递归版
void MergeSortNonR(int *arr,int length)
{int k = 1;int *temp = (int *)malloc(sizeof(int) * length);while(k < length){mergePass(arr, k, length, temp);k *= 2;}free(temp);
}void TestMergeSort()
{int a[] = { 3, 4, 6, 1, 2, 8, 0, 5, 7 };MergeSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}// O(Max(N, 范围))
// O(N+范围) 时间复杂度
// O(范围) 空间复杂度
void CountSort(int* a, int n)
{int max = a[0], min = a[0];for (int i = 0; i < n; ++i){if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}//找到数据的范围int range = max - min + 1;int* countArray = (int*)malloc(range*sizeof(int));memset(countArray, 0, sizeof(int)*range);//存放在相对位置，可以节省空间for (int i = 0; i < n; ++i){countArray[a[i] - min]++;}//可能存在重复的数据，有几个存几个int index = 0;for (int i = 0; i < range; ++i){	while (countArray[i]--){a[index++] = i+min;}}
}void TestCountSort()
{int a[] = { 3, 4, 6, 2, 8, 5, 2, 2, 9, 9, 1000000, 99999};CountSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}void TestSortOP()
{const int n = 1000000;int* a1 = (int*)malloc(sizeof(int)*n);int* a2 = (int*)malloc(sizeof(int)*n);int* a3 = (int*)malloc(sizeof(int)*n);int* a4 = (int*)malloc(sizeof(int)*n);int* a5 = (int*)malloc(sizeof(int)*n);int* a6 = (int*)malloc(sizeof(int)*n);int* a7 = (int*)malloc(sizeof(int)*n);int* a8 = (int*)malloc(sizeof(int)*n);srand(time(0));for (int i = 0; i < n; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}a8[n] = 100000000;size_t begin1 = clock();//InsertSort(a1, n);size_t end1 = clock();printf("%u\n", end1 - begin1);size_t begin2 = clock();ShellSort(a2, n);size_t end2 = clock();printf("%u\n", end2 - begin2);size_t begin3 = clock();//SelectSort(a3, n);size_t end3 = clock();printf("%u\n", end3 - begin3);size_t begin4 = clock();HeapSort(a4, n);size_t end4 = clock();printf("%u\n", end4 - begin4);size_t begin5 = clock();//BubbleSort(a5, n);size_t end5 = clock();printf("%u\n", end5 - begin5);size_t begin6 = clock();QuickSort(a6, 0, n-1);size_t end6 = clock();printf("%u\n", end6 - begin6);size_t begin7 = clock();MergeSort(a7, n);size_t end7 = clock();printf("%u\n", end7 - begin7);size_t begin8 = clock();CountSort(a8, n);size_t end8 = clock();printf("%u\n", end8 - begin8);
}

11.题目：

912. 排序数组

答案